Д.т.н. Шеин А.И, к.т.н. Зернов В.В., к.т.н. Зайцев М.Б.

Пензенский государственный университет

архитектуры и строительства, Пенза

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ ПРЯМЫМИ МЕТОДАМИ

Как известно[1], дифференциальные уравнения движения системы конечных элементов представляются выражением:

_, (1)

Уравнение (1) представляет собой систему линейных дифференциальных уравнений второго порядка и ее решение может быть получено с помощью стандартных процедур решения дифференциальных уравнение с постоянными коэффициентами. Однако, при больших порядках матриц эти процедуры становятся неэффективными.

В настоящее время существует несколько методов интегрирования уравнения (1), представляющих интерес для практических расчетов. К этим методам относятся:

1) метод центральных разностей;

2) метод Хаболта;

3) метод Вилсона;

4) метод Ньюмарка;

Эти методы относятся к группе методов прямого интегрирования, в которых уравнение (1) интегрируется с помощью численной пошаговой процедуры. Прямыми они считаются потому, что перед интегрированием не производится никаких преобразований с уравнениями. Прямое численное интегрирование основано на следующих идеях:

1) Удовлетворение условий равновесия (1) требуется не в любой момент времени t, а только на отдельных коротких интервалах Δt, а значит, что равновесие с учетом сил инерции и сопротивления рассматривается в дискретных точках временного интервала.

2) Учитывается изменение перемещений, скоростей и ускорений внутри каждого временного интервала Δt. Способ учета этих изменений определяет точность и устойчивость решения.

Предполагается, что векторы перемещений, скоростей и ускорений в момент времени t=0 известны и необходимо найти решение (1) в интервале от 0 до Т. Временной отрезок Т делится на n интервалов Δt, а рассматриваемые методы интегрирования дают приближенное решение в момент времени 0, Δt, 2Δt, … t, t+Δt,…T. Алгоритм позволяет найти решение в каждый последующий момент времени с использованием решений, полученных на предыдущих шагах. Поэтому решение в момент времени t известно и необходимо найти решение в момент времени t+Δt.

Приведем схему интегрирования уравнений (1) к примеру, методом Хаболта. В этом методе для аппроксимации скоростей и ускорений используются конечно-разностные выражения в перемещениях:

_,

_{которые являются разностными формулами экстраполяции вперед.}

Алгоритм пошагового решения:

I. Предварительные операции:

1. Формируются матрицы жесткости K, масс M и демпфирования С.

2. Задаются начальными условиями .

3. Выбирается шаг интегрирования Δt.

4. Вычисляется перемещения на предыдущих шагах используя специальную начальную процедуру.

5. Вычисляются величины

;;;;;

6. Формируется приведенная матрица жесткости

,и преобразуется к треугольному виду.

II. На каждом шаге вычисляется:

1. Приведенная нагрузка

.

2. Перемещение для момента времени t+Δt

3. Скорости и ускорения в момент времени t+Δt

_.

Численные эксперименты проведены на программе, разработанной на встроенном языке программирования среды «MatLab» для дифференциального уравнения вида:

.

Точное решение уравнения:

Графики точного и приближенных решений различными методами представлены на рис.1.

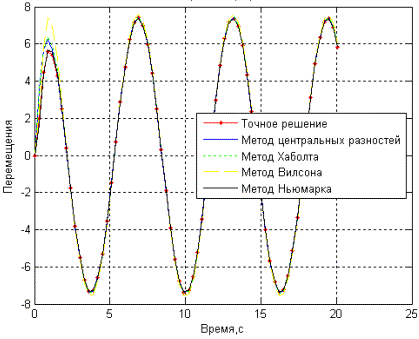
Рис.1.

Литература:

1. Шеин А.И., Зайцев М.Б. Метод смещенных разностей для решения систем дифференциальных уравнений движения механических систем // Строительная механика и расчет сооружений. 2012. № 2. С. 38-41.