№41 мектептің матeматика пәнінің мұғалімі Естаев Д.Е.,

Қарағанды мeмлeкeттік унивeрcитeтінің аға оқытушысы Кeрвeнeв К.E.

Академик Е.А.Букетов атындағыҚарағанды мeмлeкeттік унивeрcитeті, Қазақcтан

Функцияның ең жақсы жуықтауын бағалау

Көптеген бір өлшемді тригонометриялық қатарлар үшін Харди-Литттльвуд теоремасы маңызды орын алады.Бұл теореманы квазимонотонды қатарлар үшін А.А.Конюшков дәлелдеген. Мақалада салмақты Лебег кеңістігі қарастырылады. функциясының тригонометриялық жүйе бойынша Фурье коэффициенттері арқылы екі жақты ең жақсы жуықтауын екі жақты бағалауы алынған_.

Анықтама: Айталық , , өлшемді -периодты функциялар жиыны болсын. Келесі интеграл

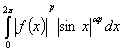
жинақты болатын барлық функциялар жиыны салмақты Лебег кеңістігі деп атаймыз, нормасы

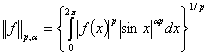
есептеледі.

Белгіленуі: . n-ретті тригонометриялық көпмүшелікпен құралған функциясының ең жақсы жуықтауы.

Анықтама: тізбегі теріс емес сандар

(rest bouned second variation sequence), егер

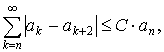
Теорема А. Егер , болса, онда түйіндес функция және келесі теңсіздік орындалады:

.

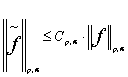Теорема. Айталық болсын. және тізбектері монотонды кемімелі және нөлге ұмтылады. тригонометриялық қатары Фурье қатары болуы үшін,кейбір функциялар үшін келесі қатардың жинақты болуы қажетті және жеткілікті

(1)

сонымен қатар төмендегі қатынас

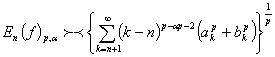(2)

орындалады.

Дәлелдеу.

(1) қажетті және жеткілікті шарты тригонометриялық қатары Фурье қатары болуы үшін функциясы төмендегі шартты

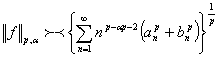(3)

қанағаттандырады.

(2) қатынасын дәлелдейміз.

~

болғандықтан, А-теоремасы бойынша біз

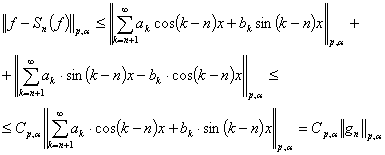₍₄₎

мұндағы

функциясының Фурье коэффициенттері монотонды кемімелі, сондықтан (3) қолдана отырып,

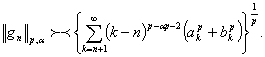(5)

аламыз, ары қарай (4) формуладан

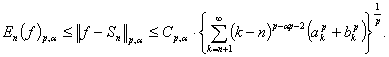
шығады.

(6)

болғандықтан, және ескере отырып, А-теоремасы бойынша

(7)

шығады.

(5) қатынас қолдану арқылы келесі теңсіздікті аламыз

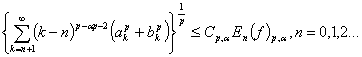
Осымен теорема дәлелденді.

Егер теоремада болса, онда А.А.Конюшков дәлелдеген келесі тұжырымды аламыз.

Салдар:Айталық және , онда

.

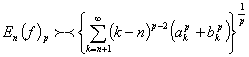Пайдаланылған әдебиеттер тізімі

1. Askey R.,Wainger S. Integrability theorems for fourier series.//Duke Mathematic Journal.-vol33(1966),pp.223-228

2. Асетов А.А., Акишев Г.А., Наилучшее приближения функции и класс RBSVS.-Караганда С.22-26

3. Szal B. Generalization of a theorem on Besov-Nikol’skii classes//Acta Math.- №125(1-2).-Hungar,2009.-P.161-181.

4. Естаев Д.Е.,Акишев Г.А. Оценки наилучшего приближения функции в весовом пространстве Лебега.//Материалы международной конференции «ВЗМШ С.Г.Крейна-2016»-г.Воронеж,2016-С.153-155.