Педагогические науки/ 5. Современные методы преподавания

К.ф.-м.н. Искакова А.С., Жаксыбаева Г.К.

Евразийский национальный университет имени Л.Н. Гумилева, Казахстан

Методические аспекты решений задач на вероятность в средней школе с использованием системы Matlab

Естественный процесс приобретения опыта является одним из самых важных понятий в изучении математики на уровне средней школы [1]. Особенно в области теории вероятностей учащимся не хватает практики с явлениями случайности. К сожалению, без понимания этого явления учащиеся не вникнут в «теорию» и их знания будут носить формальный характер [2-4]. Например, такое явление как «шанс» вполне уместно можно объяснить на подбрасывании монеты, кости, раскрутки рулетки, вытягивание карты из колоды и др. На данных примерах урок можно начать следующими вопросами: Какая сумма очков чаще всего получается, если две кости подброшены несколько раз подряд? Какова вероятность получения трех гербов при трехразовом подбрасывании монеты? В ходе такой постановки вопроса, после выполнения определенного числа опытов, учащиеся сравнивают результаты между собой и формулируют гипотезы. Практическая реализация таких опытов занимает немало учебного времени. Однако, если к этому делу привлечь компьютеры, то эксперименты могут быть смоделированы очень быстро [5-6]. То есть, имеет место практическая значимость компьютерного применения на уроках по темам теории вероятностей.

В системе Matlab генератор случайных чисел RAND, как выше было отмечено в других приложениях, вполне применим для имитации подбрасывании монеты, кости, раскрутки рулетки или вытаскивании карты из колоды. Также учащиеся знакомятся с основной структурой Matlab программирования, такой как условные операторы и операторы цикла. С целью сохранения данных из имитационных экспериментов, учащиеся узнают, как обращаться с переменными и массивами. И, наконец, они делают знакомство с визуализации их результатов с помощью графического инструмента Mаtlab.

При решении проблем с помощью компьютерного моделирования, учащиеся понимают несколько основных принципов, касающихся относительной частоты исходов случайных экспериментов. После этой предварительной стадии, студенты готовы изучить соответствующие темы из теории вероятностей.

В силу теории когнитивного процесса, описанного в разделе 2, особое внимание уделяется выбору проблем мотивации. Прежде, чем объявить новый предлог или теорему, один или несколько примеров решаются с помощью метода компьютерного моделирования. В таких случаях учащиеся обычно обнаруживают идею перед учителем.

К сожалению, в средней школе учебные планы на тему «Независимые события» проходят по желанию и, из-за ограниченного количества учебных часов, они часто пропускаются. Однако, без введения понятия независимых событий, многие элементарные задачи имеют довольно сложное решение. Например, важное понятие схемы Бернулли, которая имеет множество практических применений основано на идеях независимых испытаний и умножения вероятностей.

Приведем пример решения задачи методом компьютерного программирования и теоретическим соображением.

Пример . Заключенный в тюрьме приговорен к смертной казни. К счастью, надзиратель предлагает заключенному шанс выжить. Надзиратель дает заключенному 12 черных шаров и 12 белых шаров, две урны и говорит ему, что завтра палач будет случайным образом выбирать урну и из него вытянет один шар случайным образом. Если будет вытянут белый шар, то заключенный будет освобожден, если черный шар будет вытянут, то приговор будет осуществлен. Как заключенный должен расположить шары в урнах, чтобы максимизировать свой шанс на свободу?

Компьютерное моделирование: Алгоритм, представленный на рис 1 имитирует случайный выбор урну и шара, где в первой урне 7 шаров, из которых 4 белые.

Учащиеся имеют множество возможностей поэкспериментировать с этим алгоритмом. Они могут изменять значения переменных k и i и попытаться сформировать гипотезу о том, при каких значениях этих переменных заключенный имеет наибольшие шансы быть освобождены

Теоретическое решение: Предположим, что ни одна из урн не является пустой. Если , например заключенный в первую урну положит k шаров, из из которых i белые, то вторая урна должна содержать 24 - k шаров, из которых 12 - i белые. Пусть А - событие "вытаскивание шар белого цвета", U₁ - событие "палач выбирает первую урну" и U₂ - событие "палач выбирает вторую урну". Так как U₂является "дополнение" из U₁, мы можем применить теорему полной вероятности получить.

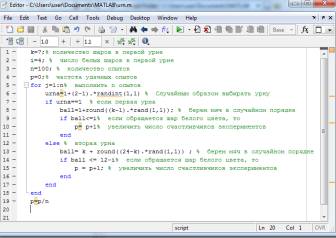
Рис. 1. Случайный выбор урны и шара при количестве шаров в первой урне 7, из которых 4 белые.

Обозначим через Р(k,i)=P(A), чтобы подчеркнуть, что P(A) является функцией двух переменных, то есть k = 1, ..., 24 и i = 0, 1, ..., 12. За исключением формального доказательства учащиеся также могут использовать другие аргументы. Они могут, например, подсчитать все возможные значения Р(k,i), используя систему Matlab, нарисовать 3D график этой функции в Matlab т.д. Целесообразно, если все эти возможности обсуждаются и сравниваются в классе вместе с формальным доказательством того, что максимум этой функции P(1,1)=0,739.

На рис. 2-3 представлен алгоритм, вычисляющий максимальную вероятность выигрыша.

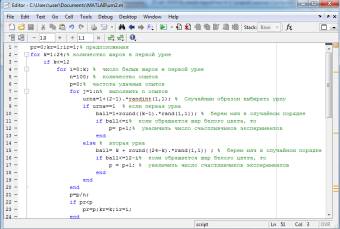
Рис. 2. Алгоритм, вычисляющий максимальную вероятность выигрыша.

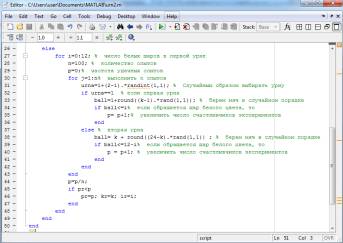
Рис. 3. Продолжение алгоритма, вычисляющий максимальную вероятность выигрыша.

Таким образом, компьютерное программирование при изучении вероятностных тем обогащают процесс обучения, позволяют сделать обучение более эффективным, а также способствуют творческому развитию учащихся. В системе среднего образования использование новейших информационных технических средств обучения создает благоприятные условия для развития мотивации и формирования личности школьника, его активное участие в учебном процессе обеспечивает комфортную эмоциональную атмосферу на уроке.

ЛИТЕРАТУРА

1. Искакова А., Байтугелова Н., Шарипбаева А. Сравнительный анализ нормативно-бюджетного финансирования среднего образования современных зарубежных стран // Вестник ЕНУ им. Л.Н. Гумилева, Серия гуманитарных наукы, 2016, №1 (110).- С.191-199.

2. Anand P. G., Ross S. M. Using computer-assisted instruction to personalize arithmetic materials for elementary school children //Journal of educational psychology. – 1987. – Т. 79. – №. 1. – С. 72.

3. Marbach‐Ad G., Rotbain Y., Stavy R. Using computer animation and illustration activities to improve high school students' achievement in molecular genetics //Journal of Research in Science Teaching. – 2008. – Т. 45. – №. 3. – С. 273-292.

4. Greer M., Lin L., Atkinson R. K. Using a computer game to teach school-aged children about asthma //Interactive Learning Environments. – 2016. – С. 1-8.

5. Antoch J., Cihák M., Pelzla G. F. M. Teaching probability at secondary schools using computers.// International Statistical Institute, 56th Session, 2007: Jaromfr Antoch, Michal Cihßk. – 8 p.

6. Kurtulmuş F., Ünal H. Discriminating rapeseed varieties using computer vision and machine learning //Expert Systems with Applications. – 2015. – Т. 42. – №. 4. – С. 1880-1891.