Алдибекова К.А.,

магистр технических наук

Преподаватель лицея при КазГАСА

МЕТОД ОБНАРУЖЕНИЯ ПЕШЕХОДОВ МЕТОД HOG.

В данной статье рассматривается научная новизна, выявляющая проблемы и обоснование условий формирования структуры системы распознавания образов методом SURF. В этом методе используется нормализацию перекрывающегося локального контраста для увеличения точности.

Бұл мақалада SURF әдісі арқылы бейнені тану жүйесінің құрылымын қалыптастыру шарттарының проблемалары және негіздеуін анықтауға мүмкіндік беретін ғылыми жаңалық қаралады. Бұл әдіс жоғары дәлдікпен жергілікті контрастты қосарлас қалыпқа пайдаланады.

This article describes the scientific novelty; identify problems and justification of the conditions of formation of structure of the system to recognize images by SURF. This method uses the normalization of overlapping local contrast to increase accuracy.

Гистограмма направленных градиентов (англ. Histogram of Oriented Gradients, HOG) — дескрипторы особых точек, которые используются в компьютерном зрениии обработке изображений с целью распознавания объектов. Данная техника основана на подсчете количества направлений градиента в локальных областях изображения. Этот метод похож на гистограммы направления края, дескрипторы SIFT и контексты формы, но отличается тем, что вычисляется на плотной сетке равномерно распределенных ячеек и использует нормализацию перекрывающегося локального контраста для увеличения точности.

Навнит Далал и Билл Триггс, исследователи INRIA, впервые описали гистограмму направленных градиентов в своей работе на CVPR в июне 2005 года. В этой работе они использовали алгоритм для нахождения пешеходов на статичных изображениях, хотя впоследствии расширили область применения до нахождения людей на видео, а также различных животных и машин на статичных изображениях.

Основной идеей алгоритма является допущение, что внешний вид и форма объекта на участке изображения могут быть описаны распределением градиентов интенсивности или направлением краев. Реализация этих дескрипторов может быть произведена путем разделения изображения на маленькие связные области, именуемые ячейками, и расчетом для каждой ячейки гистограммы направлений градиентов или направлений краев для пикселов, находящихся внутри ячейки. Комбинация этих гистограмм и является дескриптором. Для увеличения точности локальные гистограммы подвергаются нормализации по контрасту. С этой целью вычисляется мера интенсивности на большем фрагменте изображения, который называется блоком, и полученное значение используется для нормализации. Нормализованные дескрипторы обладают лучшей инвариантностью по отношению к освещению.

Дескриптор HOG имеет несколько преимуществ над другими дескрипторами. Поскольку HOG работает локально, метод поддерживает инвариантность геометрических и фотометрических преобразований, за исключением ориентации объекта. Подобные изменения появятся только в больших фрагментах изображения. Более того, как обнаружили Далал и Триггс, грубое разбиение пространства, точное вычисление направлений и сильная локальная фотометрическая нормализация позволяют игнорировать движения пешеходов, если они поддерживают вертикальное положение тела. Дескриптор HOG, таким образом, является хорошим средством нахождения людей на изображениях.

Реализация алгоритма. Вычисление градиента.

Первым шагом вычислений во многих детекторах особых точек является нормализация цвета и гамма-коррекция. Далал и Триггс установили, что для дескриптора HOG этот шаг можно опустить, поскольку последующая нормализация даст тот же результат. Поэтому на первом шаге рассчитываются значения градиентов. Самым распространенным методом является применение одномерной дифференцирующей маски в горизонтальном и/или вертикальном направлении. Этот метод требует фильтрации цветовой или яркостной составляющей при помощи следующих фильтрующих ядер:

[-1, 0, 1] и [-1, 0, 1]^Т

Далал и Триггс использовали более сложные маски, такие как Собел 3x3 (Оператор Собеля) или диагональные маски, но эти маски показали более низкую производительность для данной задачи. Они также экспериментировали с размытием по Гауссу перед применением дифференцирующей маски, но также обнаружили, что пропуск этого шага увеличивает быстродействие без заметной потери качества.

Группировка направлений.

На следующем шаге вычисляются гистограммы ячеек. Каждый пиксел в ячейке участвует во взвешенном голосовании для каналов гистограммы направлений, основанном на значении градиентов. Ячейки могут быть прямоугольной или круглой формы, каналы гистограммы равномерно распределяются от 0 до 180 или же от 0 до 360 градусов, в зависимости от того, вычисляется "знаковый" или "беззнаковый градиент". Далал и Триггс обнаружили, что беззнаковый градиент совместно с девятью каналами гистограммы дает лучшие результаты при распознавании людей. При распределении весов в голосовании вес пикселя может задаваться либо абсолютным значением градиента, либо некоторой функцией от него; в реальных тестах абсолютное значение градиента дает лучшие результаты. Другими возможными вариантами могут быть квадратный корень, квадрат или урезанное абсолютное значение градиента.

Блоки дескрипторов.

Для принятия во внимания яркости и контрастности градиенты следует локально нормировать, для чего ячейки нужно сгруппировать в более крупные связные блоки. Дескриптор HOG, таким образом, является вектором компонент нормированных гистограмм ячеек из всех областей блока. Как правило, блоки перекрываются, то есть каждая ячейка входит более чем в один конечный дескриптор. Используются две основные геометрии блока: прямоугольные R-HOG и круглые C-HOG. Блоки R-HOG обычно являются квадратными сетками, характеризующимися тремя параметрами: количеством ячеек на блок, количеством пикселов на ячейку и количеством каналов на гистограмму ячейки. В эксперименте Далала и Триггса оптимальными параметрами являются блоки 3x3, ячейки 6x6 и 9 каналов на гистограмму. Более того, они обнаружили, что можно слегка повысить скорость вычислений, применяя гауссов фильтр внутри каждого блока до процедуры голосования, что, в свою очередь, снижает вес пикселей на границах блоков. Блоки R-HOG оказываются очень похожими на SIFT-дескрипторы; однако, несмотря на их похожую структуру, блоки R-HOG вычисляются на плотных сетках фиксированного масштаба без фиксированного направления, в то время как SIFT-дескрипторы вычисляются в разреженных, не чувствительных к масштабу ключевых точках изображения и используют поворот для выравнивания направления. Кроме того, для кодирования информации о форме объектов блоки R-HOG используются совместно, в то время как SIFT-дескрипторы используются по отдельности.

Блоки C-HOG имеют 2 разновидности: с цельной центральной ячейкой и разделенной на сектора. Эти блоки могут быть описаны 4 параметрами: количество секторов и колец, радиус центрального кольца и коэффициент расширения для радиусов остальных колец. Далал и Триггс обнаружили, что обе разновидности показали одинаковый результат, и разделение на 2 кольца и 4 сектора с радиусом 4 пиксела и коэффициентом расширения 2 дало лучший результат в их эксперименте. Кроме того, гауссово взвешивание не дало никаких улучшений при использовании блоков C-HOG. Эти блоки похожи на контексты формы, но имеют важное отличие: блоки C-HOG содержат ячейки с несколькими каналами направлений, в то время как контексты формы используют только наличие одного края.

Нормализация блоков.

Далал и Триггс исследовали четыре метода нормализации блоков. Пусть — ненормированный вектор, содержащий все гистограммы данного блока, $Описание: \|v\|_k$ — его k-норма, при и — некая малая константа (точное значение не так важно). Тогда нормировочный множитель можно получить одним из следующих способов:

L2-норма:

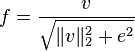
$Описание: f = {v \over \sqrt{\|v\|^2_2+e^2}}$

L2-hys: L2-норма ограничивается сверху (значения v, большие 0,2, полагаются равными 0,2) и перенормируется, как в L1-норма:

$Описание: f = {v \over (\|v\|_1+e)}$

Корень из L1-нормы:

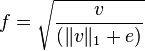
$Описание: f = \sqrt{v \over (\|v\|_1+e)}$

Далал и Триггс установили, что L1-норма дает менее надежные результаты, чем остальные три, которые работают приблизительно одинаково хорошо, однако все четыре метода значительно улучшают результаты по сравнению с ненормализованными.

Заключение

Возможность математической постановки ранее не формализованных и

решающихся на интуитивном уровне задач обусловила важность и перспективность применения методов распознавания широким кругом специалистов: математиками, инженерами, социологами, геологами, медиками и т.д.

Несмотря на большое разнообразие методов, и подходов к распознаванию образов, в настоящее время не существует единого универсального алгоритма, позволяющего решить задачу классификации объектов.

Конечно, каждый метод имеет свои недостатки и преимущества, но при совместном их использовании результаты распознавания образов могут быть значительно улучшены.

Список использованной литературы

1. Алдибекова К.А., магистр технических наук, преподаватель лицея при КазГАСА «Распознавание образов методом SURF», XII international scientific and practical conference "cutting-edge science - 2016", volum. Office 1, velocity tower, 10 st. Mary’s gate, sheffield, s yorkshire, england, s1 4lr.

2. Журавлев Ю.И. Об алгебраическом подходе к решению задач распознавания или классификации // Проблемы кибернетики. М.: Наука, 2005. - Вып. 33. С. 5-68.

3. Ryuji Funayama, Hiromichi Yanagihara, Luc Van Gool, Tinne Tuytelaars, Herbert Bay, "ROBUST INTEREST POINT DETECTOR AND DESCRIPTOR", published 2009-09-24

4. N. Dalal and B. Triggs. Histograms of oriented gradients for human detection // Conference on Computer Vision and Pattern Recognition (CVPR), 2005.

5. D. Geronimo, A.M. Lopez, A.D. Sappa, and T. Graf. Survey of pedestrian detection for advanced driver assistance systems // Pattern Analysis and Machine Intelligence, 2010.

6. «Теория распознавания образов (статистические проблемы обучения)», В. Н. Вапник, А. Я. Червоненкис. Издательство «Наука», Главная редакция физико-математической литературы, М., 1974, 416 стр