Механика

А.А. Танирбергенова, М.А. Берикбаева

Карагандинский государственный технический университет, Казахстан

Расчет надежности механических

систем типа цепи

Для расчета надежности последовательно соединенных стержней обычно применяется модель «слабого звена». По этой модели рассчитывается статически определяемая стержневая система или цепь, состоящая из элементов. Пусть плотность распределения напряжения в ом элементе. Для цепи напряжения во всех элементах одинаковы; для стержневой системы закон распределения напряжений одинаков, но различается параметрами. Если функцию распределения предельного напряжения обозначим через то вероятность не разрушения го элемента, при условии, что напряжение в нём равно будет равна . Интегрируя это выражение по всевозможным значениям напряжения, найдём безусловную вероятность не разрушения го элемента

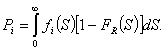(1)

Теперь вероятность безотказной работы системы определяется перемножением соответствующих вероятностей найдем вероятность безотказной работы системы

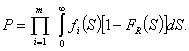(2)

Если напряжения в элементах не случайны, то

(3)

где – дельта функция Дирака.

Если напряжения в элементах одинаковы, то вместо (3) получаем

(4)

Пусть напряжение во всех элементах одинаково, но не является случайной величиной. Тогда трактуя выражение (4) как условную вероятность, можно записать

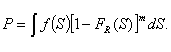(5)

Эту формулу легко получить, пологая , , где функция распределения минимального значения выборки

. (6)

Если предельное напряжение подчиняется распределению Вейбулла

,

То вместо формул (3) – (5) получим соответственно

; ;

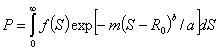. (7)

Теперь положим, что стержни изготовлены из различных материалов. Тогда обобщением формул (2) и (3) являются соответственно следующие выражения:

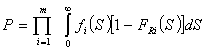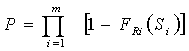; ; (8)

а вместо формулы (5) получим

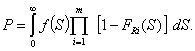(9)

Пусть действующее и предельное напряжение в стержнях имеют нормальное распределение. Тогда вероятность безотказной работы (ВБР) определяется по формуле

, (10)

где или .

Если действующее и предельное напряжениев стержнях имеют логарифмически нормальное распределение, то получаем вновь выражения Если учитывая соотношения (10), а также зависимость между параметрами логарифмически нормального распределения и численными характеристиками случайных величин, находим

,

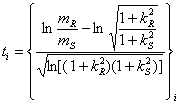где , коэффициенты вариации.

Чаще всего для определения надежности стержневых систем при последовательном соединении применяется формула (5). она предполагает, что напряжения во всех стержнях одинаковы, но случайны, а несущая способность всех стержней одинакова. В таких условиях работают также цепи, зубчатое колесо, в которых элементами являются звенья и зубья. Определения надежности по этим формулам в общем случае требует численного интегрирования и при больших «» возможно только на ЭВМ.

Если в этих формулах напряжение распределено по нормальному закону, то можно использовать приближенный метод определния надежности системы, предложенный в работе . Идея метода состоит в аппроксимации закона распределениянесущей способности системы нормальным законом так, чтобы он был близок истинному в диапазоне пониженных значений несущей способности системы, так как именно эти значения определяют надежность системы.

литература

1. Бакиров Ж.Б., Танирбергенова А.А. Расчет надежности многоэлементных систем на основе статических модулей. // Материали за VIІ международна научнапрактична конференция «Ключови въпроси в съвременната наука 2011» Том 38, Технологии. - София, 2011.

8. Бакиров Ж.Б., Танирбергенова А.А. Оптимизация конструкций по надежности // Материалы IX международной научно – практической конференций «Европейская наука ХХI века – 2013» Том 29, Техническая наука. – 7-15 мая 2013, Przemys¹l, Nauka i studia 2013.