Saidmurod
Sangovich Nazarov, Senior Teacher of the
chair “Mechanization of Processing of Agricultural Production and
Cattle-farms”, Tajik Agrarian University. Tajikistan.
Victor
Alexeyevich Muhin, Doctor of Technical
Sciences, Professor, Head of the chair “Mechfnization and Technology of
Stock-breeding”, Saratov State Agrarian University in honor of N.I.Vavilov.
Russia.
Andrey
Anatolyevich Zhizdyuk, Candidate of Technical
Sciences. Russia.
THE DIFFERENTIAL EQUATION OF RELATIVE MOTION FOR PARTICLES OF THE FEED RESIDUES
The article shows a diagram of
a rotational ellipsoid brush cleaner and shows the principle of operation of
the device. Theoretical studies of the dependence between the design parameters
of the rotary ellipsoidal brush cleaner and kinematic motions parameters of
feed residues particles. Determined relative velocity of particles is given and
an analytical solution of the equations about motion of a forage particles
residues (impurities). As a result these theoretical studies will allow in the
future undertaking the development of an installation for cleaning feeders.
Keywords:
Rotary
ellipsoidal brush cleaner, equations about motion of
forage particles residues (impurities), fodder rests,
blades, feeder, animal products, relative velocity of the particles.
After feeding the
animals, according to our observations, feeding remains a certain amount of
waste, these wastes reach 8-10% distributed forage, i.e. 300-400 kg in the
cowshed on 200 goals. Wastes
consist of different types of particles, from dry dust to wet stem. Uneaten
food mixed with distributed feed and worsen its quality, which ultimately
affects the productivity of animals. This is due to the hygiene of obtaining
animal products. Impurities impair the sanitary condition of the feeders, can
cause food poisoning and contribute to the spread of pathogenic microbes. So after each feeding trough must be thoroughly cleaned.
In this paper, we theoretical studies given the
dependence between the design parameters of the rotary ellipsoidal brush cleaner
and kinematic parameters of motion of particles of feed residues.
![]()
flexible shaft
![]()
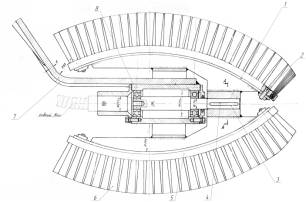
Figure 1 - The scheme is
a rotational ellipsoid brush cleaner
The scheme is a
rotational ellipsoid brush cleaner shown in figure 1. The cleaning brush
consists of four blades. Brush blades are fixed to the casing 1 two screws 2 at
both ends. The casing is fitted on the shaft 3 by the key 4. Pads 5 of the
brushes are made from aluminium. Tufts of the brushes 6 of nylon filament 1.2
mm thick with diameter of brush 8 mm start. They form the blade. [1]
The shaft is
mounted in the bracket 7 in two radial-thrust bearings 8 inclined to the
horizontal and intersecting surfaces. Brush mounted above the trough bottom so
that its blade in contact with him get fit.
In the process of
cleaning a rotating ellipsoidal rotating brush moves toward the remnants of
feed at the bottom. Keep
blade brushes are shifted, and then released, picked up by the air flow through
the pneumatic transport serves in the cart.
In our case, the
process of movement of particles on the blades, located radially. Waste feeding will make
complex motion: relative on the blades and rotational. General theory of motion
of particles on rotary surfaces taking into account all the resistance forces
developed by academician P. M. Vasilenko. [2]
the Foundations of this theory and were adopted in the analysis of movement of
particles of the investigated material on the blades (figure 2).
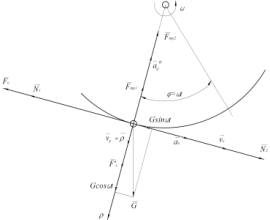
Figure
2 - Dynamic diagram of the forces acting on the particle feed residues
Draw up the differential
equation of the relative motion of the particles of feed residues through a
rotating ellipsoidal brush cleaner. [3]
![]() , (1)
, (1)
where m – weight of particulate food residues,
kg; G – the force of gravity, N;
,
– the friction forces that depend on the action of gravity and of inertial forces kriolitovyjj, N;
– karaliova the inertial force, N;
– carrying the force of inertia, N.
The differential
equation of the relative motion after the transformation of equation (1) has
the form:
![]() , (2)
, (2)
where ![]() – the angular velocity of the
ellipsoid, rad/s; t – the adventures of the particles along the arc of the
ellipsoid, s.
– the angular velocity of the
ellipsoid, rad/s; t – the adventures of the particles along the arc of the
ellipsoid, s.
The force of
gravity is equal to:
G = mg, (3)
where g –the acceleration of gravity, m/s2.Friction force that depends on normal pressure N1 (including gravity):
Fòð1 = f N1 , (4)
where f1 – coefficient of friction; N1 – normal pressure, N.Normal pressure is equal to:
. (5)
Equation (4) with (5) has the form:
Fòð1 = f1
. (6)
Friction Fòð2 taking into account of the Coriolis forceis equal to:
Fòð2 = f2 N2 . (7)
The normal pressure N2 is:
. (8)
The Coriolis force is equal to:
, (9)
where– relative velocity, m/s;
– Coriolis acceleration of particles, m/s2,
.
Then the equation (7) with (9) is equal to:
Fòð2 = f2
. (10)
Carrying the force of inertia is equal to:
, (11)
where- portable centripetal acceleration, m/s2.
Then we have:
. (12)
After some transformations of equation (2) are as follows:
. (13)
Reducing weight (m) are:
. (14)
The differential equation has the form:
. (15)
Solution of these equations has the form:
; (16)
For
:
; (17)
; (18)
; (19)
; (20)
; (21)
. (22)
The second solution:
. (23)
Then we have the equations of motion:
. (24)
Differentiating with respect to time, are:
(25)
When t = 0
. (26)
; (27)
; (28)
. (29)
; (30)
; (31)
; (32)
; (33)
; (34)
The coefficients are equal:
; (35)
; (36)
. (37)
The relative velocity of the particles:
. (38)
An analytical solution to the equations of motion of the particles of the feed residues (impurities) and determined the relative velocity of the particles. These indicators will allow us to develop installations for cleaning feeders.
References
1. Nazarov, S.S., V.A. Muhin, N. Shamsiev, A.A. Zhizdyuk and H. Zaidov, 2008. Rotacionno-jellipsoidnyj shhetochnyj ochistitel' [A rotational-ellipsoidal brush cleaner. The registration certificate of intellectual product], 081TJ (81/08), pp:2.
2. Vasilenko, P.M., 1960. Teorija dvizhenija chasticy po sherohovatym poverhnostjam sel'skohozjajstvennyh mashin [The theory of motion of particles on rough surfaces agricultural machines] Kiev: Izdatel'stvo Akademii s/h nauk, pp: 284.
3. Muhin, V.A., A.A. Zhizdyuk and S.S. Nazarov, 2009. The differential eauation of relative particles’ movement of the fodder rests. The Bulletin of Saratov State Agrarian University named after N.I. Vavilov, 5: 61-65.