Технические науки. Обработка материалов в машиностроении

Бестужева О.В.

ФГБОУ ВО "Белгородский государственный технологический университет им. В.Г. Шухова"

Исследование зависимости площади среза от технологических параметров и режимов ротационной обработки крупногабаритной детали

Для производства цемента применяются различное крупногабаритное оборудование – вращающиеся сушильные, обжиговые печи, шаровые трубные мельницы. Одним из главных факторов повышения производительности работы является надежность, зависящая от качества монтажных работ, своевременного ремонта и технического обслуживания, которые являются наиболее трудоемкими, но слабо оснащенными.

Основными конструктивными элементами мельниц являются барабан, загрузочное и разгрузочное устройства, подшипники, на которые опирается барабан мельницы, и привод, состоящий из электродвигателя и редуктора. Барабаны мельниц изготовляют из стальных листов и с двух сторон имеют крышки с цапфами, которые выполняют роль несущих узлов, а также служат для загрузки и выгрузки продукции.

Исследуя наружные поверхности цапфы установлено, что из-за постоянных динамических нагрузок, приводящих к возникновению вибраций, вследствие их несоосности и неуравновешенности, изменяется форма цапфы. В процессе эксплуатации формируются определенные наследственные дефекты, которые вызывают повышенный износ цапф, в результате чего появляется износ поверхности скольжения. Цапфа теряет наружную цилиндрическую форму и, как частный случай, приобретает форму поверхности, близкую к усеченному конусу.

Наиболее прогрессивным является способ восстановления работоспособности приставным станком на месте эксплуатации [1, 2, 3]. В процессе обработки, а также последующей эксплуатации, поверхности подвергают механической обработке с использованием специального переносного станка, состоящего из силового стола с закрепленным на нем кубом, суппорта с установленным ротационным резцом, и механизма самоустановки стоек для базирования деталей [4, 5].

Разработана математическая модель процесса ротационного резания [6, 7], основой которой является вычисление действительной площади среза, а также ее зависимости от технологических и геометрических параметров, что в свою очередь позволит установить оптимальные значения технологических режимов для формирования цилиндрической поверхности с использованием приставного станка.

Рассмотрим влияние углов установки, режимов резания, заточки и радиуса режущей чаши на площадь поверхности среза при обработке детали в форме усеченного конуса. Рассматриваемая деталь имеет форму усеченного конуса, у которого R₀ – радиус большего основания, а r₀ – радиус меньшего основания. Усеченный конус достраиваем до полного конуса, как показано на рисунке 1.

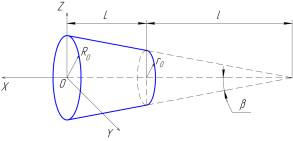
Рисунок 1 - Расчетная схема для составления уравнения усеченного конуса

Для нахождения аналитического выражения, определяющего уравнение конуса с основанием R₀ и высотой L+l введем декартову систему координат XYZ с центром в точке О, расположенной на оси симметрии (см. рисунок 1) конуса. Уравнение рассматриваемого конуса в выбранной системе координат будет иметь вид:

. (1)

Согласно расчетной схеме, представленной на рисунке 1, получаем следующий результат:

. (2)

Подстановка (2) в уравнение конуса (1) позволяет получить следующий результат:

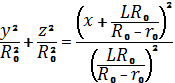. (3)

Для нахождения уравнения режущей чашки, введем декартову систему координат X’Y’Z’ (см. рисунок 2) с центром в точке О’ на оси симметрии основания конической чаши.

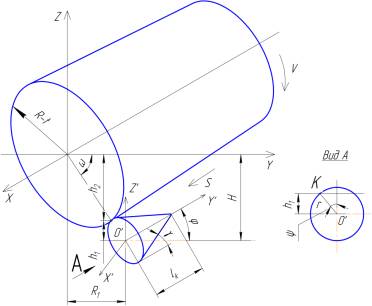
Рисунок 2 - Расчетная схема расположения режущей чаши относительно обрабатываемой детали в системе координат X’Y’Z’

В данной системе координат уравнение режущей чаши в виде усеченного конуса можно записать в следующем виде:

, (4)

где r – радиус режущей чаши,

l_k – высота конуса, полученного в результате дополнительного построения на базе режущей чаши.

Рассмотри закон преобразования двумерной системы координат XOYв результате поворота последней на некоторый произвольный угол φ. В результате поворота получаем двумерную систему координат X’ОY’.

Согласно расчетной схеме, представленной на рисунке 3, можно получить следующее соотношение:

(5)

, (6)

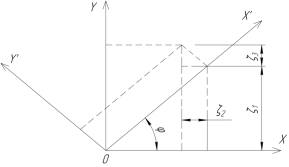
Рисунок 3 - Расчетная схема для нахождения закона преобразования двумерной системы координат при повороте

Обратное преобразование при переходе от двумерной системы XОY к системе X’ОY’ можно получить если величину угла заменить на значение -, тогда находим:

, (7)

. (8)

Перенесем путем параллельного переноса, начало координат декартовой системы X’ОY’Z’ из точки O’ в точку О. В результате данного преобразования соотношение (4) преобразуется к следующему виду:

, (9)

где согласно расчетной схеме, представленной на рисунке 2, находим, что: , , , , ,

здесь – угол отклонения радиуса контакта обрабатываемой детали с окружностью режущей чаши от плоскости XОY;

ψ – угол, образованной радиусом режущей чаши, проведенной в точку K контакта с обрабатываемой деталью и осью OZ.

На основании расчетной схемы, представленной на рисунке 1, можно установить закон изменения величины радиуса контакта при продвижении вдоль оси симметрии усеченного конуса обрабатываемой детали:

, (10)

где введенная величина изменяется в пределах .

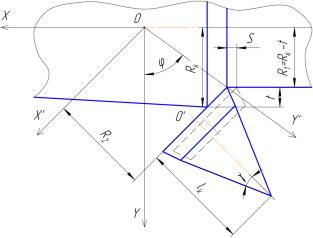
Рисунок 4 - Расчетная схема для определения параметров преобразования при повороте системы координат X’ОY’ вокруг оси ОZ

Согласно расчетной схеме, представленной на рисунке 4, находим:

. (11)

Произведем поворот системы координат X’ОY’ вокруг оси ОZ на угол –. В результате данного преобразования (см. рисунок 4) система координат X’ОY’ совпадет с системой координат XОY, а уравнение чаши ротационного конуса примет следующий вид:

, (12)

Согласно (7), (8), (9), (10):

, (13)

. (14)

Подстановка полученных выражений в (12) приводит к следующему выражению:

(15)

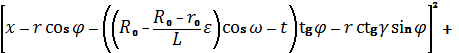
Где 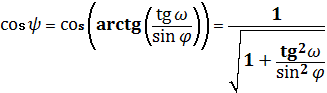(16)

Подстановка (16) в (15) позволяет окончательно получить следующее уравнение:

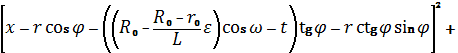
(17)

Поверхность обрабатываемой детали и поверхность режущей чашки пересекаются по кривой, аналитическое уравнение которой описывается следующей системой уравнений:

На основании выражения (18) находим:

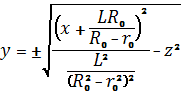. (20)

Положительное значение (20) подставляем в (17) и в результате когда z=0, кривая пересечения поверхностей обрабатываемой детали и режущей чашки проецируется на плоскость XOY в кривую следующего вида:

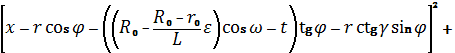
(21)

Используя (19) выражаем в явном виде значение величины z:

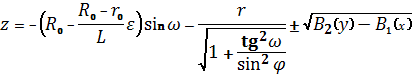, (22)

где введены следующие обозначения:

, (23)

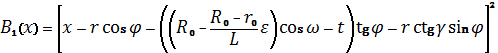(24)

В выражении (22) выбираем соотношение с положительным знаком и вычисляем:

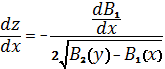, (25)

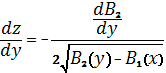, (26)

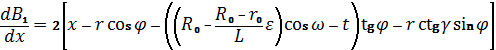, (27)

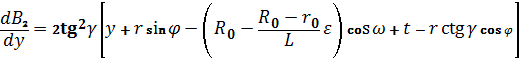,(28)

С учетом выражений (23) и (24) соотношения (27) и (28) можно привести к следующему виду:

, (28)

. (29)

Площадь поверхности среза режущей чашкой за один проход можно определить на основании следующего соотношения:

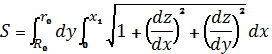, (30)

где – корень уравнения (21).

Вычислим:

. (31)

Подстановка (31) в (30) позволяет получить формулу площади поверхности среза :

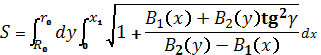. (32)

Таким образом, полученные соотношения позволяют вычислить площадь поверхности среза режущей чашей, которая образуется при одном проходе обработки детали в форме усеченного конуса.

В результате вычислений, получен график изменения площади поверхности среза при изменении радиуса режущей чашки, движущейся вдоль поверхности обрабатываемой детали.

Анализ проведенных зависимостей показывает, что графики носят монотонно возрастающий характер при изменения параметров резания.

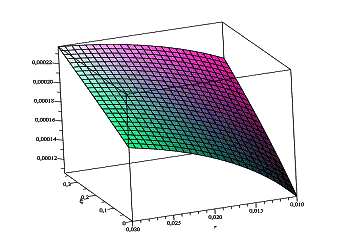
Рисунок 5 - Изменения площади поверхности среза режущей чашей при изменении параметра ξ и радиуса режущей чаши при фиксированных значениях ω=1,56 φ=Pi/3, γ=Pi/4

Литература:

1. Патент на полезную модель № 2003113096/02, 05.05.2003 Бондаренко Ю.А., Федоренко М.А. Способ обработки крупногабаритных валов без их демонтажа // Патент России № 2242346.2003.

2. Патент на полезную модель № 2008104754/22, 07.02.2008 Федоренко М.А., Бондаренко Ю.А., Федоренко Т.М. Станок для обработки цапф помольных мельниц // Патент России № 75339.2008.

3. Федоренко М.А., Санина Т.М., Бондаренко Ю.А., Погонин А.А., Схиртладзе А.Г. Бездемонтажное восстановление крупногабаритных агрегатов // Ремонт, восстановление, модернизация. 2009. № 11. С. 11-14.

4. Федоренко Т.М., Федоренко М.А., Бондаренко Ю.А. Восстановление работоспособности цапф помольных мельниц с применением переносного станка // Технология машиностроения. 2009. № 3. С. 20-21.

5. Федоренко М.А., Бондаренко Ю.А., Федоренко Т.М. Исследование обеспечения необходимой шероховатости поверхности крупногабаритных вращающихся деталей приставными станочными модулями. Вестник Белгородского государственного технологического университета им. В.Г. Шухова. 2008. №2. С. 35-38.

6. Маркова О.В. Математическая модель оптимизации обработки цилиндрических поверхностей крупногабаритного вращающегося оборудования.

7. Ящерицын П.И., Борисенко А.В., Дривотин И.Г., Лебедев В.Я. Ротационное резание материалов. Мн.: Наука и техника, 1987. 229 с.