Современные информационные технологии /1. Компьютерная
инженерия
К.т.н., доц.
Т.Б. Аждер
Московский
технологический университет, Россия
Анализ моделей прогнозирования
Модель прогнозирования на основе временных
рядов является широко распространенной. Но при случайных исходных данных
использование данных моделей, а также байесовский подход не даст ожидаемых
результатов.
Пусть требуется найти интервальную оценку
параметра 
функции 
, очные значения 
и 
наблюдать нельзя, а значения случайных величин 
и
можно: xi=ξi+δi ; yi= ηi + εi , i=1,2,…,n, где δi и εi – ошибки
значений переменных и функции.
Пусть имеем статистический ряд экспериментальных
значений {xi}
X и
соответствующий им ряд значений функций {yi}
Y, i=1,2,…,n, n≥m, где m
– число оцениваемых параметров 
.
Найдем выражение для совместной плотности
вероятности экспериментальных данных при условии, что значения ξi и ηi
связаны функциональной зависимостью, но их погрешности δi и εi – независимые при переходе от
одной точки (xi , yi)
к другой. Тогда совместная плотность вероятности случайного события получить
одновременно значения xi и yi:
,
где 
– функция
математического ожидания ξi,
экспериментальных значений xi и
параметров 
, 
– функция
математического ожидания ηi,
экспериментальных значений yi и
параметров 
.
Совместная плотность вероятности для
получения n статистически независимых
точек (xi , yi)
вычисляется по формуле
.
Функциональное соотношение 
, (1)
порождает структурное соотношение между наблюдаемыми
случайными величинами xi и yi при
аддитивных помехах δi , εi :
, или 
Пусть
экспериментальные значения xi и yi –
случайные величины, каждая из которых имеет функцию плотности вероятности,
описываемую функцией Гаусса с математическими ожиданиями ξi и ηi,
дисперсиями σ2(xi),
σ2(yi)
и коэффициентом корреляции ρi=ρ(xi,yi).
Плотность вероятности получить точку с координатами (xi , yi)
вычисляется по формуле
,
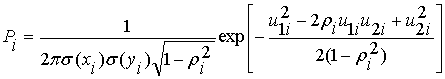где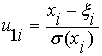 
; 
.
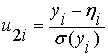Совместная
плотность вероятности получить n
независимых таких точек имеет вид 
и
lnL(X,Y)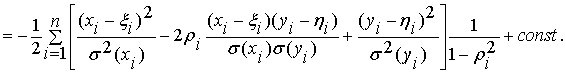
Оценки искомых параметров 
находятся из условия
минимума функционала 
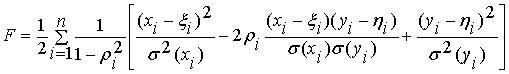(2)
Если погрешности δi и εi некоррелированы, то выражение
(2) примет вид:
.
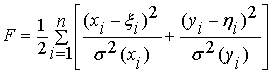(3)
Определим минимум функционала по
параметрам 
при условии (1).
Перед определением точки минимума функции
(2) по 
необходимо определить ξi .
Искомые значения ξi и
оценки 
определяются из условия
, 
.
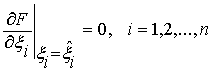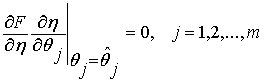Таким образом, решение задачи минимизации
функционала (2) эквивалентно решению системы уравнений
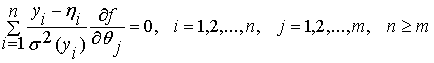(4)
при 
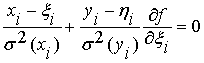(5)
Из (5)
следует, что для задачи минимальное значение функционала метода наименьших
квадратов (МНК) больше минимального значения функционала (3), т.к. условие (5)
– условие ортогональности вектора касательной к функции f(ξ, θ) в точке, принимаемой за истинную, и вектора, проведенного через две
точки: исходную (xi1, xi2, …, xin, yi) и принимаемую за истинную. Минимизация функционала
(3) при условии (1) приводит к минимизации суммы квадратов наикратчайших
расстояний от точки (xi1, xi2, …, xin, yi) до кривой, тогда как в МНК минимизируется сумма
квадратов отклонений при фиксированных значениях xij.
В задаче прогнозирования при одновременном
учете погрешности в значениях функции и в значениях аргументов классический МКМ
не так точен, как метод, основывается на конфлюэнтном анализе.
Литература:
1.
Грешилов А.А.,
Стакун В.А., Стакун А.А. Математические методы построения прогнозов. – М.:
Радио и связь, 1997.
2.
Елисеева И.И., Юзбашев М.М.
Общая теория статистики: Учебник/ Под ред. чл.-корр. РАН И.И. Елисеевой. – 4-е
изд., перераб. и доп. – М.: Финансы и статистика, 2001.
3.
Колмогоров А. Н., Фомин
С. В. Элементы теории функций и функционального анализа. – 7-е изд. – М.:
ФИЗМАТЛИТ, 2004.