SECTION 6. Computer science.

Талайбеккызы Н., Баяндиев Е.Н., Махамбетжанов Д.Б.

Таразский государственный университет им. М.Х. Дулати, Тараз, Казахстан

О некоторых алгоритмах численного решения задачи Коши для системы дифференциальных уравнений первого порядка методом Рунге-Кутта на языке DELPHI.

Пусть дана система двух дифференциальных уравнений первого порядка:

(1)

Решением системы (ф.1) называется пара функций и , при подстановке которых в систему получаются тождества:

, .

Решению

Системы уравнений(ф.1) соответствует интегральная кривая в пространсте трех измерений (). Задача Коши для системы состоит в нахождении решения системы (1), удовлетворяющего начальным условиям

, . (2)

Постановка задачи Коши для системы n дифференциальных уравнений первого порядка аналогична задаче (ф.1)-(ф.2), а именно: требуется найти решение системы

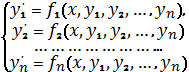(3)

при начальных начальных условиях

, , ..., . (4)

Пример. Найти численное решение задачи Коши для системы двух дифференциальных уравнений на языке Delphi

, .

Задача Коши для дифференциального уравнения второго порядка

,

приводится к задаче Коши для предыдущей системы, если обозначить

и .

Вычисления правых частей дифференциальных уравнений

ведется в программе:

unit Unit1;

interface

uses

Winapi.Windows, Winapi.Messages, System.SysUtils, System.Variants, System.Classes, Vcl.Graphics,

Vcl.Controls, Vcl.Forms, Vcl.Dialogs, Vcl.StdCtrls;

type

TForm1 = class(TForm)

Label1: TLabel;

Edit1: TEdit;

Edit2: TEdit;

Label2: TLabel;

Label3: TLabel;

Button1: TButton;

Label4: TLabel;

Edit3: TEdit;

Edit4: TEdit;

Label5: TLabel;

Label6: TLabel;

Label7: TLabel;

Edit5: TEdit;

Label8: TLabel;

Memo1: TMemo;

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

type

coef2=array[0..4,1..2] of real;

vect=array[1..2] of real;

var

Form1: TForm1; c:array[1..4] of real=(0,0.5,0.5,1);

var

i,j,n,m:integer;

a,b,h,x:real;

y,y1:vect;

k:coef2;

ch:char;

implementation

{$R *.dfm}

function f(i:integer;x:real;y:vect):real;

BEGIN

CASE 1 OF

1:f:=y[2];

2:f:=-y[1];

END;

END;

procedure TForm1.Button1Click(Sender: TObject);

begin

a:=strtofloat(edit1.Text);

b:=strtofloat(edit2.Text);

y1[1]:=strtofloat(edit3.Text);

y1[2]:=strtofloat(edit4.Text);

M:=strtoint(edit5.Text);

x:=a;

h:=(b-a)/m;

memo1.Clear;

memo1.Lines.Add('x='+floattostr(x)+' y1='+floattostr(y1[1])+' y2='+floattostr(y1[2]));

FOR i:=1 TO m DO

BEGIN

FOR j:=1 TO 4 DO

BEGIN

FOR n:=1 TO 2 DO

y[n]:=y1[n]+c[j]*k[j-1,n];

FOR n:=1 TO 2 DO

k[j,n]:=h*f(n,x+c[j]*h,y);

END;

FOR n:=1 TO 2 DO

y1[n]:=y1[n]+(k[1,n]+2*k[2,n]+2*k[3,n]+k[4,n])/6;

x:=x+h;

memo1.Lines.Add('x='+floattostr(x)+' y1='+floattostr(y1[1])+' y2='+floattostr(y1[2]));

END;

end;

end.

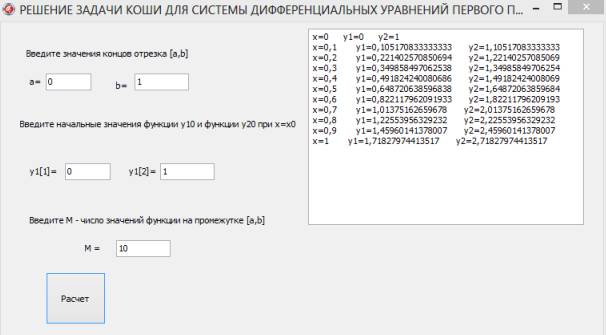
Рисунок 1 – Разработанная программа.

Описанные алгоритмы и разработанная программа (Рис.1) может быть использованна в различных исследованиях основанных на данном методе Рунге-Кутта, а также в процессе преподавания в университетах в качестве лабораторных работ.

Литература

1. Пушкарь Е.А.Дифференциальные уравнения в задачах и примерах.М.:2007.-С.146

2. Шевцов А.Н. Математическое моделирование в прикладных задачах. Тараз 2012.-С. 26-28