Моделирование бифуркаций аттрактора Ресслера в MAPLE
Система
дифференциальных уравнений, решение которой, приводит к созданию аттрактора
Ресслера (рис. 1) имеет вид:
![]()
![]()
![]() .(1)
.(1)
Рассмотрим поведение решения системыпри изменении коэффициентовa, b.
Циклы периодов 2 и 8 соответственно
при значениях параметра![]() и
и ![]() и нерегулярный аттрактор при
и нерегулярный аттрактор при![]() .Действительно, приуказанных выше фиксированных
значениях параметров
.Действительно, приуказанных выше фиксированных
значениях параметров ![]() и
и ![]() с
увеличеваниемпараметра
с
увеличеваниемпараметра ![]() от значения
от значения ![]() до величины
до величины ![]() наблюдается
каскад бифуркаций Фейгенбаума удвоения периода (рис. 2). А при больших
значениях
наблюдается
каскад бифуркаций Фейгенбаума удвоения периода (рис. 2). А при больших
значениях ![]() и
и ![]() наблюдаются циклы соответственно периодов 5 и 3, что
свидетельствует о наличии субгармонического каскада в сценарии перехода к хаосут.е. сценарий перехода к хаосу развивается согласно
порядку Шарковского.Циклы периодов 5 и 3 соответственно при значениях параметра
наблюдаются циклы соответственно периодов 5 и 3, что
свидетельствует о наличии субгармонического каскада в сценарии перехода к хаосут.е. сценарий перехода к хаосу развивается согласно
порядку Шарковского.Циклы периодов 5 и 3 соответственно при значениях параметра
![]() и
и ![]() (рис.3).Исследование сценария перехода к хаосу в
данной системе проведем при фиксированных значениях параметров
(рис.3).Исследование сценария перехода к хаосу в
данной системе проведем при фиксированных значениях параметров ![]() и
и ![]() .
.
С ростом значений параметра ![]() в системе (1)
наблюдается каскад бифуркаций удвоения периода исходного цикла.
в системе (1)
наблюдается каскад бифуркаций удвоения периода исходного цикла.
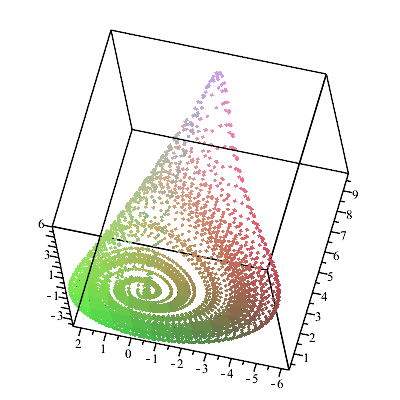 Рис.1 Модель аттрактора
Ресслера в MAPLE
Рис.1 Модель аттрактора
Ресслера в MAPLE
При a := 0.5; b := 0.75; ![]()
Трехмерное
изображение
Рис.
2
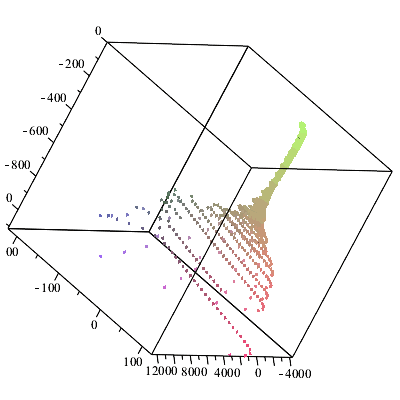
При a := 0.5; b := 0.75; ![]()
Трехмерное
изображение
Рис.
3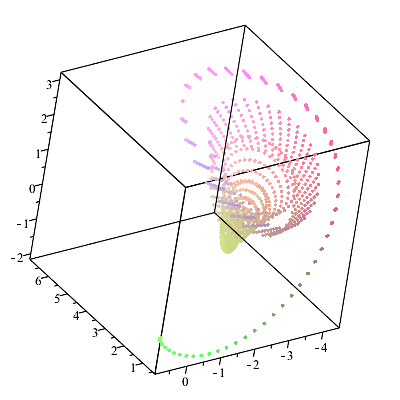
Разработанный математический алгоритм

Заключение
Таким
образом, в системах Рёсслера вида (1) переход к хаосу осуществляется через
каскады бифуркаций удвоения периода Фейгенбаума, субгармонические каскады и
гомоклинический каскад бифуркаций.
Список используемых источников
1. Н. А.
Магницкий, С. В.СидоровНОВЫЕ
МЕТОДЫ ХАОТИЧЕСКОЙ ДИНАМИКИ.
2. Итоги науки техники.
Современные проблемы математики. Фундаментальные направления. Динамические
системы.-М.: ВИНИТИ, 1985, т. 1, 243 с., т. 2, 312 с.
3. Малинецкий
Г.Г., Потапов А.Б. Современные проблемы нели¬нейной динамики. - М.: УРСС, 2002,
360 с.