Чиркова Л.Н., к.п.н.
Вятский Государственный
Университет, Россия
Некоторые свойства
полудифференцируемых функций
Рассмотрим
определения верхней и нижней производных функции в точке. Верхней производной
функции f в точке 
(по Коши) называется
величина 
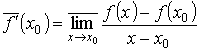. Аналогично определяется нижняя производная данной функции в
рассматриваемой точке: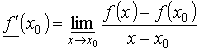 
.
Известно,
что функция 
в точке x0=0 не имеет обычной
двусторонней производной. Найдем верхнюю и нижнюю производные данной функции в
точке x0=0:
;
.
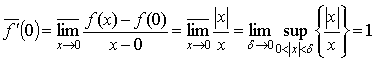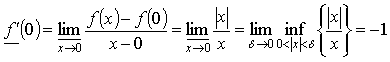Определим
понятия полудифференцируемости функции в точке сверху и снизу.
Определение 1. Функцию f будем называть полудифференцируемой сверху в точке 
, если в некоторой окрестности 
данной точки имеет
место представление 
, где 
– полунепрерывная
сверху в точке 
функция.
Определение 2. Функцию f назовем полудифференцируемой
снизу в точке 
, если в некоторой окрестности 
этой точки будет справедливо представление 
, где 
– полунепрерывная
снизу в точке 
функция.
Функции
и 
соответственно называются
верхней и нижней производными Каратеодори функции f в точке 
, где 
и 
.
Функция 
является полудифференцируемой по Каратеодори сверху и снизу в
точке x0=0. Действительно,
в качестве ее верхней и нижней производных Каратеодори достаточно рассмотреть
соответственно функции
,
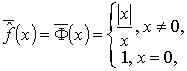
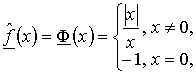являющиеся
полунепрерывными сверху и снизу в силу выполнения неравенств 
, 
.
Приведем
некоторые свойства верхних и нижних производных [1], [2].
1)
Пусть
функция f определена в некоторой окрестности 
точки 
и в этой точке является
полудифференцируемой сверху и снизу функцией. Тогда для ее верхней и нижней производных справедливо
неравенство: 
.
Докажем
свойство 1. По определениям верхней и нижней производных, а также свойству 
верхнего и нижнего
пределов функции имеем:
.
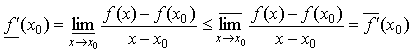2)
Пусть
функция f определена в некоторой окрестности 
точки 
и в этой точке является
полудифференцируемой сверху и снизу функцией. Тогда функция 
, где с – const, в
точке 
является
полудифференцируемой сверху функцией, при этом для ее верхней производной
справедливы равенства:
, если с>0; 
, если с<0.
Докажем
свойство 2. Пусть 
– верхняя производная
Каратеодори функции f.
Тогда в силу ее полудифференцируемости сверху в точке 
имеем:
.
Так
как функция 
при с>0 полунепрерывна сверху в точке 
, а при с<0
полунепрерывна снизу в точке 
, то полученное представление приращения 
говорит о том, что
функция 
при с>0 также полудифференцируема сверху в данной
точке, искомое соотношение следует из равенства 
; при с<0 функция
полудифференцируема снизу
в точке 
, искомое соотношение следует из равенства 
.
3)
Пусть
функции f и g определены в некоторой окрестности 
точки 
и в этой точке
являются полудифференцируемыми сверху функциями. Тогда их сумма f
+ g в точке 
также является
полудифференцируемой сверху, при этом для ее верхней производной справедлива оценка
.
Приведем
доказательство свойства 3. Пусть 
и 
– верхние производные
Каратеодори функций f и g соответственно. Тогда в силу их
полудифференцируемости сверху в точке 
имеем:
.
Так
как сумма 
есть полунепрерывная
сверху в точке 
функция, то
полученное представление приращения 
говорит о том, что
сумма f + g есть также
полудифференцируемая сверху в данной точке функция. Доказываемое соотношение
следует из неравенства
.
Это
свойство можно переформулировать и для полудифференцируемых снизу в точке 
функций с
соответствующими оценками для нижних производных их суммы: пусть функции f и g определены в некоторой окрестности 
точки 
и в этой точке
являются полудифференцируемыми снизу функциями. Тогда их сумма f + g в точке 
также является
полудифференцируемой снизу, при этом для ее нижней производной справедлива оценка:
.
Справедливы
и другие свойства для полудифференцируемых функций.
Литература:
1.
Брайчев Г. Г. Введение в теорию роста выпуклых и целых
функций. М.: Прометей, 2005. 232 с.
2.
Калинин С. И., Чиркова
Л. Н. Верхняя и нижняя производные Каратеодори в доказательствах некоторых
теорем негладкого анализа // Преподавание математики, физики, информатики в
вузах и школах: проблемы содержания, технологии и методики: Материалы V
Всероссийской науч.-практ. конф. Глазов: ООО «Глазовская типография», 2015. С.
58–60.
3.
Калинин С. И.,
Чиркова Л. Н. Негладкие функции: аспект характеризации // Математический
вестник педвузов и университетов Волго-Вятского региона: периодический
межвузовский сборник научно-методических работ. Выпуск 18. – Киров: Науч.
изд-во ВятГУ, 2016. С. 73–82.