Педагогические науки/2. Проблемы подготовки специалистов

к.ф.-м.н. Філоненко Н.В., Філоненко Ю.О.

Переяслав-Хмельницький державний педагогічний університет

імені Григорія Сковороди, Україна

ВИВЧЕННЯ ОСНОВ КОРЕЛЯЦІЙНОГО АНАЛІЗУ В КУРСІ МАТЕМАТИЧНОЇ СТАТИСТИКИ

В статті розглядаються основні положення методів кореляційного аналізу та методика вивчення даного розділу математичної статистики.

Ключові слова: кореляція, регресія, кореляційний аналіз, коефіцієнти кореляції.

Постановка проблеми. У процесі підготовки майбутнього вчителя математики одними з найважливіших є питання про роль дисциплін, завдяки вивченню яких у студентів формуються професійні знання та вміння. Методи теорії ймовірностей та математичної статистики стають все більше популярними у таких науках, як педагогіка та психологія. Пояснюється це тим, що математична статистика дає спеціалістам-практикам гарно розроблений апарат для об'єктивного аналізу результатів педагогічного і психологічного експерименту і вироблення практичних рекомендацій у даній галузі. Значну роль у підвищенні математизації таких наук, як педагогіка і психологія відіграє суцільна комп'ютеризація.

Метою статті є формування знань з основ кореляційного аналізу в межах програми курсу математичної статистики для математиків, рекомендації з розв'язування прикладних задач по темах розділу та застосування набутих знань при проведенні педагогічних експериментів; формування у студентів вміння користуватися науковою та методичною літературою з даного курсу.

Програма курсу включає наступні питання:

основні поняття регресійного та кореляційного аналізу; складання кореляційних таблиць; коефіцієнт лінійної кореляції і його властивості; оцінка коефіцієнта кореляції; коефіцієнт кореляції Браве-Пірсона; критерії значущості для коефіцієнта кореляції Браве-Пірсона; коефіцієнт рангової кореляції Спірмена; значущість коефіцієнта рангової кореляції Спірмена; коефіцієнт рангової кореляції Кендала; коефіцієнт спряженості Пірсона; значущість коефіцієнта спряженості Пірсона.

Розглянемо основні з цих понять.

Кореляційний аналіз ґрунтується на залежностях між випадковими величинами, відмінними від функціональної залежності. У тих випадках, коли значенню однієї величини відповідає цілком конкретне значення іншої величини, говорять, що між величинами існує функціональна залежність. Така залежність виражається функцією де – незалежна змінна, – залежна змінна. Прикладами функціональної залежності є залежність загального стажу роботи від стажу роботи на даному підприємстві , що виражається формулою , де – стаж роботи на даному підприємстві.

Для випадкових величин не завжди можна встановити функціональну залежність. Наприклад, ріст людини не можна встановити по її вазі, і навпаки. Так, у вибраній групі осіб об’єкти з однаковим зростом можуть мати різну вагу, наприклад:

при 180 см: 71 кг, 75 кг, 80 кг;

при 182 см: 73 кг, 76 кг, 85 кг.

Це означає, що між випадковими величинами може існувати зв'язок особливого роду, при якому певному значенню однієї величини відповідає певний розподіл значень другої величини, причому при зміні даної величини змінюється ряд розподілу другої величини. Такий зв'язок називається стохастичною, або імовірнісною залежністю між величинами.

Класичним прикладом стохастичної залежності є залежність між ростом батьків (Х) і їх дітей (У). Кожному значенню Х відповідає певний розподіл значень У, і в сукупності випадків просліджується тенденція до збільшення значень У із збільшенням значень Х.

Для дослідження стохастичної залежності вивчається двомірна вибірка виду (x₁, y₁), (x₂, y₂),…(x_n, y_n). Оскільки кожній парі значень (x_i, y_i) відповідає точка на координатній площині, можна дати наглядну графічну інтерпретацію зв’язку між двома змінними. Таке зображення називають кореляційним полем або діаграмою розсіювання.

При вивченні стохастичних залежностей розрізняють регресію і кореляцію.

Регресія – це залежність математичного сподівання (середнього значення) випадкової величини Y від величини x. Незалежна величина x може бути не обов’язково випадковою, тому будемо позначати її рядковою літерою.

Кореляція – це залежність між двома випадковими величинами X і Y, що характеризується за допомогою коефіцієнтів кореляції.

Відповідно до цих понять розрізняють кореляційний та регресійний аналіз.

Регресійний аналіз полягає у встановленні форми залежності між випадковою величиною Y і значеннями однієї або декількох змінних величин, причому останні вважаються точно заданими. Математичною моделлю такої залежності є рівняння регресії, що містить декілька невідомих параметрів. В загальному вигляді його можна записати так:

Модель може бути лінійною або нелінійною , поліноміальною та ін.. на основі вибіркових даних знаходять оцінки невідомих параметрів і перевіряють адекватність прийнятої математичної моделі експериментальним даним. Графіки, що відповідають рівнянням регресії, називають кривими регресії.

Кореляційний аналіз встановлює ступінь зв’язку між двома випадковими величинами X і Y. Існує декілька типів коефіцієнтів кореляції, застосування яких залежить від припущень про спільний розподіл величин X і Y (чи буде це нормальний двомірний розподіл, чи ні), а також від виду ознак, що вивчаються (кількісні чи якісні).

Як відомо, коефіцієнтом лінійної кореляції випадкових величин X і Y називається величина

,

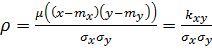а чисельник цієї рівності називається кореляційним моментом.

Коефіцієнт лінійної кореляції має такі властивості:

1. Коефіцієнт лінійної кореляції задовольняє умові .

2. Якщо , в цьому випадку між випадковими величинами X і Y відсутній лінійний кореляційний зв'язок і вони називаються некорельованими.

3. Якщо , то між випадковими величинами існує лінійний функціональний зв'язок.

4. Якщо між випадковими величинами існує лінійний функціональний зв'язок, то .

5. При має місце додатна кореляція (із збільшенням значень значення мають тенденцію до збільшення.

6. Якщо , кореляційний лінійний зв'язок між величинами зростає. Якщо , кореляційний лінійний зв'язок між величинами зменшується.

Отже, коефіцієнт кореляції ρ є мірою лінійного зв’язку між випадковими величинами.

Для двомірного нормального розподілу коефіцієнт лінійної кореляції є мірою взаємозв’язку двох випадкових величин,тому що у цьому випадку зв'язок між величинами завжди лінійний. В інших випадках рівність нулю коефіцієнта ρ може не означати відсутність кореляції, просто кореляція може бути нелінійною.

При довільному розподілі коефіцієнт лінійної кореляції є мірою тільки лінійного зв’язку. Наприклад, якщо двомірний розподіл не буде нормальним і , то коефіцієнт кореляції дорівнює 0, хоча між величинами X і Y існує функціональний зв'язок.

Останню властивість потрібно мати на увазі при використанні коефіцієнта кореляції як міри зв’язку двох випадкових величин. Тому, коли визначається коефіцієнт лінійної кореляції , як правило припускається, що експериментальні дані отримані із генеральної сукупності, що має двомірний нормальний розподіл.

Якщо недоцільно робити припущення про нормальність двомірного розподілу, як міру зв’язку часто використовують коефіцієнт рангової кореляції Спірмена, для якого вид розподілу випадкових величин X і Y не має значення. Коефіцієнт рангової кореляції є мірою будь-якої монотонної залежності між випадковими величинами.

Теоретичний коефіцієнт кореляції для генеральної сукупності як правило не відомий. На практиці коефіцієнт кореляції оцінюється по експериментальних даних, що представляють собою вибірку об’єму зв’язаних пар значень , отриману при спільному вимірюванні ознак X і Y. Вибірковий коефіцієнт кореляції прийнято позначати буквою .

Оцінкою теоретичного коефіцієнта кореляції є вибірковий коефіцієнт кореляції Браве-Пірсона. Для його визначення приймається припущення про двомірний нормальний розподіл генеральної сукупності, із якої взято вибірку. Коефіцієнт розраховується за формулою:

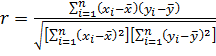, (1)

де – вибіркові середні арифметичні ознак X і Y, n – об’єм вибірки.

Для практичних розрахунків більш зручна наступна формула

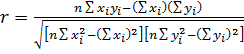, (2)

У цій формулі всі суми також обчислюються по від 1 до . Обчислення за формулою (2) дають більш точний результат, так як вона не містить середніх значень та , які як правило, є наближеними значеннями.

Приклад 1. Для даних таблиці 1 обчислити вибірковий коефіцієнт кореляції.

Таб. 1

X	1	2	3	4	5
Y	12	13	14	15	16

Розрахунки коефіцієнта кореляції зручно оформляти у вигляді таблиці.

Таб. 2

	1	12	12	1	144
	2	13	26	4	169
	3	14	42	9	196
	4	15	60	16	225
	5	16	80	25	256
	15	70	220	55	990
	225	4900	-	-	-

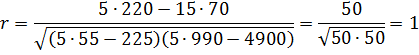
Отримавши вибірковий коефіцієнт кореляції, ще не можна робити висновок про достовірність кореляції між ознаками, особливо у тих випадках, коли ближче до 0, ніж до 1.

Для отримання правильних висновків потрібно перевірити достовірність кореляції, застосувавши критерії значущості кореляції. Ці критерії використовуються для перевірки двох гіпотез:

- нульової гіпотези, , тобто ця гіпотеза стверджує, що в генеральній сукупності відсутня кореляція, а а відмінність від нуля вибіркового коефіцієнта кореляції пояснюється тільки випадковістю вибірки.

- альтернативна гіпотеза може бути ненаправлена і направлена .

Якщо прийняте припущення про двомірний нормальний розподіл, може бути використаний Стьюдента. Для спрощення використання

у більшості підручників з математичної статистики наводиться таблиця критичних значень коефіцієнта кореляції . Достатньо порівняти вибірковий коефіцієнт кореляції з критичним значенням при рівні значущості і об’ємі вибірки . якщо, то приймається гіпотеза і робиться висновок про відсутність значущої кореляції. Якщо ж , то гіпотеза відхиляється і приймається альтернативна гіпотеза про існування статистично значущого кореляційного зв’язку.

Розглянемо наступний приклад. Приклад 2.

	5	20	100	25	400
	5	20	100	25	400
	5	21	105	25	441
	6	22	132	36	484
	7	22	154	49	484
	7	23	161	49	529
	35	128	752	209	2738
	1225	16384

.

Для прикладу 2 задаємо , вирахуване нами вибіркове значення . Оскільки , робимо висновок по існування статистично значущого кореляційного зв’язку.

Важливою властивістю коефіцієнта кореляції є те, що він не змінює свого значення ні при якому лінійному перетворенні вихідних даних та .

Наприклад, при перетворенні , значення , знайдене по перетворених даних, співпаде з , знайденим по вихідних даних.

У тих випадках, коли двомірний розподіл не є нормальним, використовується коефіцієнт рангової кореляції Спірмена :

,

де – різниця рангів і-ї пари значень та , n – об’єм вибірки.

Коефіцієнт рангової кореляції також змінюється в межах від -1 до 1. Якщо ранги строго співпадають, то . Якщо ранги розташовані строго в зворотному порядку, то . У цих випадках між величинами X і Y існує функціональна залежність, причому ця залежність не обов’язково лінійна, а може бути будь-якою монотонною залежністю. Отже, коефіцієнт рангової кореляції є мірою любої монотонної залежності між величинами X та Y.

Приклад 3.(4, с. 95)

Вивчаючи зв'язок між суб’єктивним відношенням робітників до праці (задоволеність роботою) і об’єктивним (плинність кадрів), проведено оцінку зв’язку з допомогою коефіцієнта Спірмена в «розрізі» стаж.

Групи за стажем	Індекси задоволеності роботою	Коефіцієнт плинності (%)	Ранги по X	Ранги по Y
До 5 років	0.41	26,5	5	1	4	16
5-10	0,46	15,1	4	2	2	4
10-15	0,58	3,6	3	3	0	0
15-20	0,65	3,3	2	4	2	4
Більше 20	0,73	1,3	1	5	4	16

.

.

Обчислений вибірковий коефіцієнт кореляції Спірмена також потребує перевірки на значущість. Нульова гіпотеза (генеральний коефіцієнт рангової кореляції дорівнює нулю) може бути перевірена при порівнянні вибіркового коефіцієнта кореляції з критичним значенням . Критичні значення для стандартних рівнів значущості приведені в більшості підручників з математичної статистики.

Якщо , то коефіцієнт рангової кореляції статистично незначущий на рівні значущості , якщо ж , робимо висновок про наявність значущої кореляції.

Крім коефіцієнта рангової кореляції Спірмена існує ще один коефіцієнт кореляції для даних,які проранжовані по X і по Y. Це – коефіцієнт кореляції Кендала. для підрахунку потрібно розглянути всі об’єкти вибірки попарно, число таких пар буде .

Для деякої пари констатується співпадання, якщо порядок їх рангів по X і по Y однаковий (може бути порядок натурального ряду або зворотний). Якщо порядок по X і по Y різний, констатується інверсія. Розглянемо це на прикладі . нехай маємо 8 обєктів, проранжованих по X і поY.

Об’єкти A B C D E F G H

Ранги по X 1 3 2 7 5 6 8 4

Ранги по Y 3 2 1 4 7 8 6 5

У цьому прикладі пара (A, H) дає співпадання, оскільки пари рангів (1. 4) та (3, 5) ідуть у порядку зростання. Об’єкти (D, F) дають інверсію, оскільки пари рангів (7, 6) та (4, 8) мають різний порядок.

Коефіцієнт Кендала розраховується за формулою

,

Де P – загальне число співпадань, Q – загальне число інверсій. У випадку спів падання рангів всіх об’єктів по X і по Y, , при зворотному порядку рангів . Коефіцієнт можна трактувати як різницю ймовірностей співпадання і неспівпадання порядків по обох ознаках для навгад вибраної пари.

Спрощений спосіб підрахунку наступний. Об’єкти вибірки розташовуються так, щоб їх ранги по X являли собою відрізок натурального ряду від 1 до n. Для кожного об’єкта підраховується, скільки разів його ранг по Y менший від рангів об’єктів, розташованих нижче. Доне число записується у стовпчик «співпадання». Наприклад, для А це число рівне 5. У графу «Інверсія» записується число, яке показує, від скількох рангів, розташованих нижче, є більшим даний ранг по Y. Для об’єкта А це число рівне 2. Сума співпадань дає нам число P, сума інверсій – число Q. Отримані дані записуємо в таблицю.

Вибірка	Ранги по X	Ранги по Y	Співпадання	Інверсії
A	1	3	5	2
C	2	1	6	0
B	3	2	5	0
H	4	5	3	1
E	5	7	1	2
F	6	8	0	2
D	7	4	1	0
G	8	6	0	0
Суми			P=21	Q=7

.

Література

1. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высш. шк., 2003. – 479 с.

2. Климчук В.О. Математичні методи у психології. Навчальний посібник для студентів психологічних спеціальностей. – К.: Освіта України. – 2009. – 288 с.

3. Основы математической статистики. Учебное пособие для институтов физической культуры. Под ред. В.С. Иванова.- М.: Физкультура и спорт, 1990. – 176 с.

4. Паніотто В. І., Максименко В. С., Марченко Н. М. Статистичний аналіз соціологічних даних. – К.: Вид. дім «КМ Академія», 2004. – 270 с.