Автоматизовані
системи керування на виробництві
УДК
681.5.032:622.2.629.8
Головата Ю.Б.,Роїв В.М.
ОЦІНКА СТАТИСТИЧНИХ ХАРАКТЕРИСТИК ФЛУКТУАЦІЙ ТИСКУ НА ВИХОДІ
БУРОВОГО НАСОСУ
Івано-Франківський національний технічний
університет нафти і газу
Івано-Франківськ, вул. Карпатська, 15, 76019
Golovata Yu, Roiv V.
ASSESSMENT OF THE STATISTICAL
CHARACTERISTICS OF THE PRESSURE FLUCTUATIONS AT THE OUTPUT OF DRILLING PUMP
Ivano-Frankivsk National Technical University of
Oil and Gas,
Ivano-Frankivsk, Karpatska
Str., 15, 76019
Анотація. В роботі розглядаються статистичні
характеристики тиску на виході бурового насосу як показники якості системи
автоматичного керування.
Ключові слова: тиск ,закон розподілу, математичне
сподівання
Abstract. We consider statistical characteristics of the output
pressure of drilling pump as quality automatic control system.
Key words: pressure, distribution law,
mathematical expectation.
Вступ.
Насамперед аналіз
статистичних характеристик флуктуацій тиску на виході бурового насосу є
актуальною задачею сьогодення у галузі автоматизації процесу буріння нафтових і
газових свердловин. Для оцінки даного процесу літературні джерела[1,2] не є
достатньою інформацією. Отже,
скористаємося графіком зміни тиску P(t), отриманим в результаті
експерименту на буровій Синевідне -1, праграмами Mathcad , Mathlab
та Curve Expert для визначення
математичного сподівання, дисперсії та середньоквадратичного відхилення,
ексцесу та асиметрії даної величини, а також закону розподілу, нормованої
автокореляційної функції та спектральної густини.
Виклад основного матеріалу. Із графіка,
який наведено на рисунку 1, визначаємо 41 значення тиску P(t)
і заносимо в таблицю 1. В результаті отримаємо значення сигналу P(t) через
кожні 0.05с.
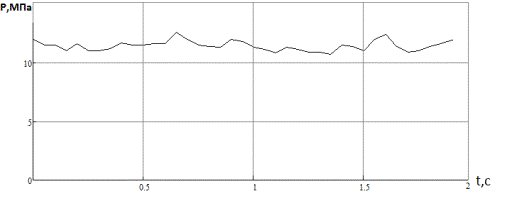
Рисунок
1 –Графік тиску P(t) на виході бурового насосу
Таблиця
1
Дискретні
значення тиску P(t)
|
t,c |
P, MПа |
t,c |
P, MПа |
t,c |
P, MПа |
t,c |
P,
MПа |
|
0 |
12 |
0,5 |
11.5 |
1 |
11.3 |
1,5 |
11 |
|
0,05 |
11.5 |
0,55 |
11.6 |
1,05 |
11.1 |
1,55 |
12 |
|
0.1 |
11.5 |
0,6 |
11.6 |
1,1 |
10.8 |
1,6 |
12.4 |
|
0,15 |
11 |
0,65 |
12.6 |
1,15 |
11.3 |
1,65 |
11.4 |
|
0,2 |
11.6 |
0,7 |
12 |
1,2 |
11.1 |
1,7 |
10.9 |
|
0,25 |
11 |
0,75 |
11.5 |
1,25 |
10.9 |
1,75 |
11 |
|
0,3 |
11 |
0,8 |
11.4 |
1,3 |
10.9 |
1,8 |
11.4 |
|
0,35 |
11.2 |
0,85 |
11.3 |
1,35 |
10.7 |
1,85 |
11.6 |
|
0,4 |
11.7 |
0,9 |
12 |
1,4 |
11.5 |
1,9 |
11.9 |
|
0,45 |
11.5 |
0,95 |
11.8 |
1,45 |
11.4 |
1,95 |
11.5 |
|
- |
- |
- |
- |
- |
- |
2 |
11 |
За допомогою програми Mathlab зробимо обробку
експериментальних даних величини P(t). В результаті отримаємо графік зміни даної величини, який
наведений на рисунку 2. Для спрощення розрахунків зміну тиску в часі – величину
P(t) позначимо функцією х у Mathlab.

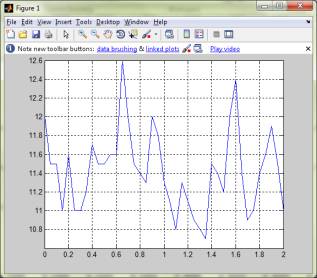
Рисунок
2 – Графік зміни тиску P(t), отриманий в результаті обробки
експериментальних даних в програмі Mathlab
Для знаходження математичного сподівання m,
дисперсії D та
середньоквадратичного відхилення σ, ексцесу kurt
(x) та
асиметрії skew(x) скористаємося
програмою MathCad:
m=11.424
D=0.18 (1)
![]()
kurt (x)= -2.009
skew(x)=
-0.0926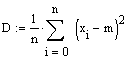
Ці характеристики визначаються законом
розподілу, який потрібно визначити.
Спочатку впорядкуємо досліджувану вибірку
у порядку зростання. Кількість інтервалів і визначаємо за формулою Стерджеса[3]:
![]() , (2)
, (2)
де
n=41 – кількість дискретних значень
досліджуваного процесу P(t);
![]()
![]()
За допомогою вбудованої функції у програмі MathCad
обчислюємо абсолютні та відносні частоти інтервалів та заносимо їх в таблицю
2.
Таблиця 2
Значення
абсолютних та відносних частот
|
Номер інтервалу |
Границя інтервалу |
Середина інтервалу xi |
Абсолютна частота mi |
Відносна частота ωi |
|
|
Нижня |
верхня |
||||
|
0 |
10.7 |
11.017 |
10.858 |
3 |
0.073 |
|
1 |
11.017 |
11.334 |
11.175 |
7 |
0.171 |
|
2 |
11.334 |
11.651 |
11.492 |
15 |
0.366 |
|
3 |
11.651 |
11.968 |
11.809 |
10 |
0.244 |
|
4 |
11.968 |
12.285 |
12.127 |
4 |
0.098 |
|
5 |
12.285 |
12.602 |
12.444 |
2 |
0.049 |
Будуємо гістограму густини даної функції попередньо
отриманих значень відносних частот, яка зображена на рисунку 3.
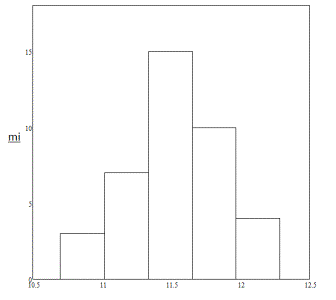
Рисунок 3 –
Гістограма густини відносних частот для тиску P(t) в
програмі Mathcad
Відтворимо закон розподілу експериментальної величини P(t)
у програмі Curve Expert.
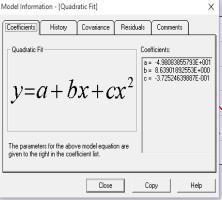
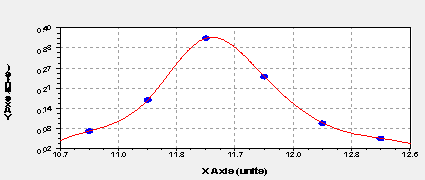
Рисунок
4 – Закон розподілу для тиску P(t) в програмі Curve Expert
По
рис/4 і розрахунках
ексцесу і асиметрії можна припустити, що даний розподіл підпорядковується
нормальному закону розподілу, оскільки kurt(x)=
-2.009, skew(x)=
-0.0926
Визначимо
автокореляційну функцію, яка охарактеризує інтенсивність зміни тиску в часі.
Для цього скористаємося формулою[2]:
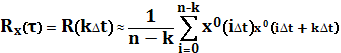 , (3)
, (3)
де: ![]() – центровані значення.
– центровані значення.
З
розрахунків за допомогою програми Mathcad отримуємо
графік нормованої автокореляційної функції тиску ![]() :
:
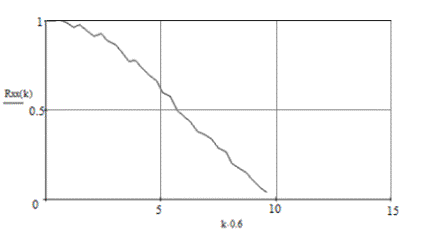
Рисунок 5 –
Графік нормованої автокореляційної функції тиску ![]()
При дослідженні даного процесу слід також
побудувати графік спектральної густини тиску на виході бурового насосу. Він
наведений на рисунку 6.
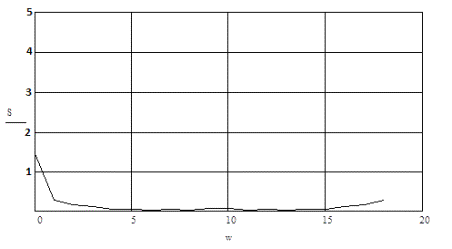
Рисунок 6 –
Графік спектральної густини тиску P(t)
Враховуючи значення заданого діапазону
зміни тиску, отриманого в процесі роботи закону розподілу, а також значення
розмаху експериментальної величини P(t), було
вибрано гаусову функцію належності тиску для фазифікації даного процесу.
Розраховуємо кількість термів Т за формулою[4,5]:
Т = 2m
+ 1, (4)
де m – кількість
розмахів послідовності накопичених відхилень контрольованого параметра.
Будуємо гаусову функцію належності тиску
в середовищі Mathlab:
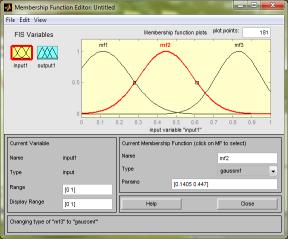
Рисунок
7 – Гаусова функція належності P(t) програмі Mathlab
Висновок. На основі графіку зміни
тиску на виході бурового насосу досліджено та визначено статистичні
характеристики флуктуацій тиску. Це
дозволило встановити, що досліджуваний процес є стаціонарним і ергодичним, має
нормальний закон розподілу і для його фазифікації може бути використана гаусова
функція належності.
Література:
1.Горбійчук М.І. Моделювання та
ідентифікація процесу заглиблення свердловин / М.І. Горбійчук, В.Б.
Кропивницька // Науковий вісник Івано-Франківського національного технічного
університету нафти і газу. – 2004. – №1(7). – С. 9-13.
2. Семенцов Г.Н. Аналіз зв’язків показників
процесу буріння на засадах системного підходу / Г.Н.Семенцов, О.В.Гутак //
Нафтогазова енергетика, №2(11) . – 2009. – С. 94-100.
3.Формула Стерджесса [Електронний ресурс] – Режим доступу: http://univer-nn.ru/zadachi-po-statistike-primeri/gruppirovka-formula-sterdzhessa/
4. Семенцов Г.Н. Метод вибоу кількості
термів для нечіткого опису базових змінних в F- перетворенні
параметрів і показників процесу буріння свердловин / Г.Н. Семенцов, О.В. Фадєєва // Вісник
Хмельницького університету №4, 2005./ Ч.1, Т.1. – С. 30-35.
5. Семенцов
Г.Н. Формування шкал лінгвістичних термів для вхідних сигналів нечітких
пристроїв контролю параметрів процесу буріння свердловин на нафту і газ / Г.Н. Семенцов, О.В. Фадєєва // Академический
вестник , №17-18, 2006 . – С. 31-35.