Технические науки/4. Транспорт
Проф. Спиридонов Э.С., Якименко Ю.Б., Набивач В.С., Яцышен
А.М.
ФГБОУ ВО «Московский
государственный университет путей
сообщения Императора Николая II» (МИИТ), Россия
Актуальность
проблемы технического перевооружения на транспорте и в транспортном
строительстве
Техническое
перевооружение фирм и отраслей народного хозяйства в целом имеет
цель;
- создать
предпосылки для развития экономики страны и реализации федеральных программ
социально-экономического развития в условиях рыночной системы хозяйствования;
- обновить
техническое оснащение и повысить конкурентоспособность организаций и
предприятий на рынке контрактов.
На
современном этапе структурной перестройки экономики России техническое
перевооружение является средством глубоких преобразований во всех сферах
производства и потребления продукции. Новые ориентиры и концепции
экономического развития привели к новым требованиям в области механизации.
Нестабильное состояние инвестиционной политики, и объемов финансирования
взаимосвязаны с низким техническим уровнем фирм. Парки машин и оборудования
имеют повышенный моральный износ и не соответствуют требованиям современных
контрактов. Техническое перевооружение - актуальная проблема и для
машиностроения, так как характеристики выпускаемых машин не соответствуют
мировому уровню.
Управление
техническим перевооружением как раз и должно обеспечить переход к качественно
новому состоянию технического оснащения фирм и его обновлению при структурной
перестройке экономики. Ее современное развитие может основываться только на
наукоемких технических и технологических решениях.
Организация обновления основных фондов зависит от отраслевой
специфики. Строительный комплекс относится к наиболее сложным отраслям
народного хозяйства. Если в промышленном производстве предмет, орудия труда и
трудовые ресурсы находятся в определенной пространственной структуре и
устойчивых условиях производства, то на строительных, особенно линейных объектах
(например, в железнодорожном, автодорожном и трубопроводном строительстве)
подрядные подразделения должны перемещаться, условия применения орудий труда
постоянно меняются в пространстве и времени. В этих условиях машинный парк
должен быть организован как система, структура и взаимосвязи которой наиболее
эффективно соответствуют производственной программе. В этом соответствии - две
стороны; условия производства и возможности его механизации.
Применение новейших информационных технологий, а именно, универсальной
системы компьютерной математики MathcadPro,
предоставило
возможность графической интерпретации поведения системы на значительно большем
временном интервале. В данном разделе информация представлена в виде распечаток
системы MathcadPro.
Исходная система дифференциальных уравнений А. И. Колмогорова и ее
решение приведены ниже (1) и (2).
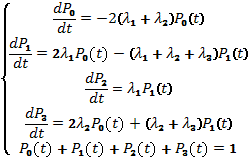
(1)
(2)
Исходные данные:
- интенсивность
возникновения неисправностей и накопления дефектов влюбом гидроизоляционном
ковре, в течение 6 лет, (1/год);
- интенсивность
возникновения неисправностей и накопления дефектов втеплоизоляционном слое, в
течение 10 лет, (1/год);
- интенсивность разрушения железобетонной панели,
в течение 20 лет, (1/год);
Вариант №1. Независимое решение в
MathcadPro системы
дифференциальных уравнений А. И. Колмогорова методом Рунге-Кутта.
t0:= 0; t1:=15 - временной интервал (15 лет);
N: = 15 - число шагов; - вектор начальных условии
Система
дифференциальных уравнений А. Н. Колмогорова:
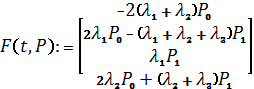
- задание решения.
Решение дифференциальных уравнений А. Н. Колмогорова выполнено с помощью
универсальной системы компьютерной математики MathcadPro методом Рунге-Кутта путем возвращения матрицы решений системы
обыкновенных дифференциальных уравнений с начальными условиями в векторе V0, правые части которых записаны в символьном
векторе F на интервале от t0 до t1 при фиксированном
числе шагов N.
Таблица 1. Матрица
состояний
tPo(t) p,(t) Р:<t>Рз(0)
|
|
t |
P0(t) |
P1(t) |
P2(t) |
P3(t) |
|
|
0 |
1 |
2 |
3 |
4 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0.587 |
0.218 |
0.021 |
0.174 |
|
2 |
2 |
0.345 |
0.287 |
0.065 |
0.304 |
|
3 |
3 |
0.202 |
0.284 |
0.113 |
0.401 |
|
4 |
4 |
0.119 |
0.251 |
0.158 |
0.473 |
|
5 |
5 |
0.07 |
0.209 |
0.196 |
0.525 |
|
6 |
6 |
0.041 |
0.167 |
0.227 |
0.564 |
|
W= |
7 |
7 |
0.024 |
0.131 |
0.252 |
0.593 |
|
8 |
8 |
0.014 |
0.1 |
0.271 |
0.614 |
|
9 |
9 |
8.271-10-3 |
0.076 |
0.286 |
0.629 |
|
10 |
10 |
4.855-10-3 |
0.057 |
0.297 |
0.641 |
|
11 |
11 |
2.85-10
-3 |
0.043 |
0.305 |
0.649 |
|
12 |
12 |
1.673-10
-3 |
0.032 |
0.312 |
0.655 |
|
13 |
13 |
9.819-10
-4 |
0.024 |
0.316 |
0.659 |
|
14 |
14 |
5.763-10
-4 |
0.017 |
0.32 |
0.662 |
|
15 |
15 |
3.383-10
-4 |
0.013 |
0.322 |
0.665 |
На рис. 1. в качестве результатов анализа
представлены графики изменений значений вероятностей пребывания кровли в
состояниях S0-S3, где:
S0- все элементы кровли в
момент времени t работоспособны,
S1 - в защитном слое
рубероида или в рулонном ковре в момент времени tвозникли дефекты,
S2 - состояние, когда в
момент tи защитный слой рубероида, и рулонный ковер одновременно не
выполняют своих функций,
S3 - снижение
теплоизоляционных свойств утеплителя в момент времени t превысило
допустимый предел.
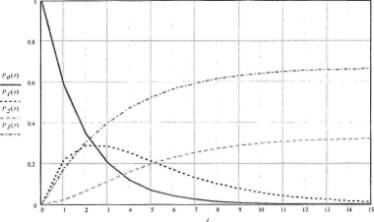
Рис. 1. Графики изменений вероятностей пребывания кровли в
состояниях S0-S3.
На рис. 2. представлен график изменения величины вероятности
отказа кровли через tлет эксплуатации.
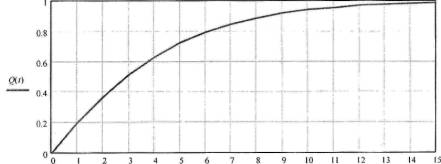
Рис. 2. График изменения величины вероятности отказа кровли через tлет эксплуатации
На графиках, построенных программным средством:
Q(t):= P2(t) + P3(t)- вероятность отказа кровли через tлет эксплуатации;
Рp:= Р2(t) + P3(t) - вероятность разборки
кровли при очередном ремонте.
На рис. 3. представлен график изменения вероятности разборки
кровли при очередном ремонте в зависимости от назначенного межремонтного
периода.
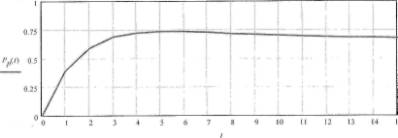
Рис. 3. График изменения вероятности разборки кровли при очередном
ремонте в зависимости от назначенного межремонтного периода
Таблица 2
Параметры Q(t):= P2(t) + P3(t)и Рр:= Р2 (t)+P3(t)
|
|
0 |
|
|
0 |
|
0 |
0 |
0 |
0 |
|
|
1 |
0.195 |
1 |
0.392 |
|
|
2 |
0.369 |
2 |
0.591 |
|
|
3 |
0.514 |
3 |
0.685 |
|
|
4 |
0.63 |
4 |
0.723 |
|
|
5 |
0.722 |
5 |
0.734 |
|
|
6 |
0.792 |
6 |
0.732 |
|
|
Q(t) = |
Q(t) = 7 |
0.845 |
Pp(t) = |
7 |
0.724 |
|
8 |
0.885 |
|
8 |
0.714 |
|
9 |
0.915 |
9 |
0.706 |
|
|
10 |
0.938 |
10 |
0.698 |
|
|
11 |
0.954 |
11 |
0.692 |
|
|
12 |
0.966 |
12 |
0.687 |
|
|
13 |
0.975 |
13 |
0.683 |
|
|
14 |
0.982 |
14 |
0.68 |
|
|
15 |
0.987 |
15 |
0.678 |
|
Вариант №2. Уточнение исходного решения при помощи информационной технологии MathcadPro.
t:=0..15 - временной интервал (15 лет);
Система функций
Таблица 3
Вероятности нахождения
кровли в каждом состоянии
|
t= |
|
P0(t)= |
|
Р1(1) = |
|
Р 2(0 = |
|
Р3«)
= |
|
1 |
|
0.587 |
|
0.218 |
|
-0.039 |
|
0.234 |
|
2 |
0.344 |
0.287 |
0.047 |
0.322 |
||||
|
3 |
0.202 |
0.284 |
0.113 |
0.401 |
||||
|
4 |
0.118 |
0.251 |
0.163 |
0.467 |
||||
|
5 |
0.069 |
0.209 |
0.202 |
0.519 |
||||
|
6 |
0.041 |
0.167 |
0.232 |
0.56 |
||||
|
7 |
0.024 |
0.131 |
0.255 |
0.591 |
||||
|
8 |
0.014 |
0.101 |
0.272 |
0.613 |
||||
|
9 |
8.23-10-3 |
0.076 |
0.285 |
0.63 |
||||
|
10 |
4.828-10-3 |
0.057 |
0.296 |
0.642 |
||||
|
11 |
2.832 10-3 |
0.043 |
0.303 |
0.651 |
||||
|
12 |
1.662-10-3 |
0.032 |
0.309 |
0.657 |
||||
|
13 |
9.747 10-4 |
0.024 |
0.314 |
0.662 |
||||
|
14 |
5.718-10-4 |
0.017 |
0.317 |
0.665 |
||||
|
15 |
3.355-10-4 |
0.013 |
0.32 |
0.667 |
По аналогии с вариантом №1 программным средством были
автоматически построены графики изменений вероятностей пребывания кровли в
состояниях S0-S1, изменения вероятности отказа через t лет
эксплуатации и изменения вероятности разборки кровли при очередном ремонте в
зависимости от назначенной продолжительности межремонтного периода. Результаты
вариантов №1 и №2 оказались достаточно близкими, поэтому графики варианта №2 и
таблица параметров состояний не показаны.
Результаты расчетов, выполненных с применением современных
информационных технологий, хорошо совпадают с результатами старых расчетов.
Прогнозные расчеты продолжительностей межремонтных периодов можно
выполнять заблаговременно на ранних этапах жизненного цикла здания или
сооружения, а именно, на стадиях проектирования и строительства. Таким образом,
можно установить и регламентировать требования к состоянию строительного
производства, к его организации, управлению, технологиям в будущем при выполнении
будущих ремонтов эксплуатируемых зданий и сооружений.
Продолжительность межремонтных периодов
зависит от того, как снижается надежность (безотказность) конструкции
вследствие снижения надежности и роста отказов ее элементов.
Рассмотрим решение задачи на примере более долговечной
конструкции, а именно, стенки здания.
Стенка здания (рис.4) состоит из защитного покрытия (элемент №1,
срок службы - 10 лет), гидроизоляционного слоя (элемент №2, срок службы - 1
лет), слоя тепло-пароизоляции, объединенной с железобетонной плитой (элемент
№3, срок службы - 20 лет).
Рис. 4.
Конструкция стенки здания.
Список используемой литературы
1. Вентцель Е. С.
Исследование операций: задачи, принципы, методология. - М.: Наука, 1980.-208 с.
2. Григорьев Э. П.
Система принятия решений ГРИАКС // ВИНИТИ РАН -1999. - №8, С. 27-33.
3. Гусаков А. А.,
Ильин Н. И. и др. (под ред. Гусакова А. А.) Экспертные системы в проектировании
и управлении строительством-М.: Стройиздат. 1995. 296 с.
4. Технология
железнодорожного строительства. Учебник для ВУЗов / Э.С Спиридонов, А. М.
Призмазонов, А. Ф. Акуратов, Т. В. Шепитько. Под ред. А. М. Призмазонова, Э. С.
Спиридонова - М.: Желдориздат, 2003. - 63 1 с.
5. Шепитько Т. В. Управление надежностью реализации
принятых решений и мониторинг производственной ситуации // Ресурсосберегающие
технологии на железнодорожном транспорте II Труды третьей научно- практической
конференции,- М.: МИИТ, 2000,- 298 с. С, IX - 4