Ñîâðåìåííûå èíôîðìàöèîííûå
òåõíîëîãèè/Êîìïüþòåðíàÿ èíæåíåðèÿ
Myasischev A.A.
Khmelnitsky National University, Ukraine
COMPUTING CAPABILITIES STM32F429I-DISCO
FOR MATRIX MULTIPLICATION
Unmanned cars are building on the
autonomous management system. Driving is the automatic and performed
using optical sensors, navigation systems, computer algorithms. Solution of these problems is performed in real time
and requires a high speed. Currently
available powerful 32-bit microcontrollers STM32 with embedded coprocessor. In the work discusses computational capabilities of the
microcontroller STM23F429ZIT6. It is installed on the board STM32F429I-DISCO
[1]. The microcontroller has a 2 MB Flash memory, 256 Kbytes of RAM and runs at
a frequency of 180 MHz. The board STM32F429I-DISCO installed SDRAM memory of
64 Mbps. In the paper compared the time of calculation of matrix multiplication
for the microcontroller and the PC with a processor AMD Phenom II X6 1090T (3,2GHz).
It uses one core. The
result of the work is to be displayed on the LCD screen, as shown in Figure 1.
Entering initial
data performed with the touch panel display. The keyboard is
programmatically created and displayed at the bottom of the display. The input
format:
724, 724, 120, 45, 700
At the end of the input click on the region CL.
Here:
724 - dimension of the square matrices (C = A * B);
724,120 - row and column indices of the first element of the matrix C (Ñ[724][120]), which is displayed on the screen;
45,700
- row and column indices of the second element of C (C [45] [700]), which is
displayed on the screen.
Figure 1 shows the output of the
calculation results and the board STM32F429I-DISCO.

Fig.1. STM32F429I-DISCO
To
solve the problem, you need to install the software packages IAR Embedded
Workbench for ARM, ST-LINK/V2 USB driver for Windows, STSW-STM32138[2]. The
test program is based on the project Touch Panel.eww, which is included in the
file STSW-STM32138.
Formation
of the keyboard on the touch - panel is performed in two stages (Figure 2):
1. We build the
keyboard at the bottom of the screen. This makes the function void
TP_Config()[2];
2. At the beginning
while () loop allocated separate areas touch panel. Each area corresponds to
its character. Figure 2 shows the coordinates of the zones.
The functions working with fonts,
lines, color settings are presented in a file stm32f429i_discovery_lcd.c. For
example, the function
LCD_DrawLine(1,
250, 239, LCD_DIR_HORIZONTAL) - draws a line in the horizontal direction length
of 239 pixels with coordinates x=1, y=250 pixels.
Function
LCD_SetFont(&Font8x12),
LCD_SetTextColor(LCD_COLOR_RED)
- set the font size of 8x12, which will display
the red.
Function
LCD_DisplayChar(LCD_LINE_11, 14, 0x30)
- displays the symbol 0 on 11 string with the
coordinates x = 14.
Function
LCD_DisplayStringLine(LINE(30),
(uint8_t*)" Matrix
multiplication");
- displays the string ‘Matrix multiplication’ on
30 line.
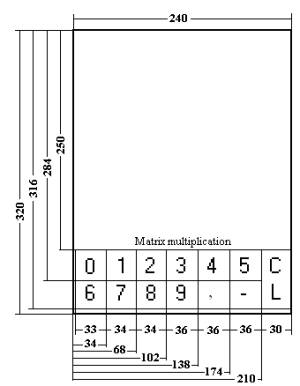
Fig.2. The
coordinates of the zones
The multiplication
of two square matrices is performed in two ways:
1. According
to the standard algorithm in accordance with the well-known program in FORTRAN
do 2 i=1,n
do 2 j=1,n
cc(i,j)=0.
do 3 k=1,n
3
cc(i,j)=cc(i,j)+aa(i,k)*bb(k,j)
2
continue
2. According
to the algorithm with the substitution of the linear array to increase the
speed with SDRAM
do 2 i=1,n
do m=1,n
a(m)=aa(i,m)
end do
do 2 j=1,n
cc(i,j)=0.
do 3 k=1,n
3
cc(i,j)=cc(i,j)+a(k)*bb(k,j)
2
continue
The
program uses one-dimensional arrays instead of two-dimensional arrays with the
substitution indexes:
cc(i,j) = cc(i +
(j-1)*n)
There I, j - array
indices, n - the size of a square matrix.
A real number is
written to SDRAM by command
*(float*) (a
+4*(i+(j-1)*n)) = 23.890
Here
a – the address of
the first memory cell SDRAM. From this address has consistently recorded the
entire one-dimensional array. The program of this address is set as
follows:
#define a
0xD0100000
4 - array index is
multiplied by 4, as a real number takes 4 bytes in memory.
23.890 - arbitrary
real number, which is recorded at the cell with index i,j
The
program for each of the three matrices (aa, bb and cc) allocates 0x2000000
(2097152) bytes of memory. The maximum number of items
one-dimensional array will be equal to 2097152/4 = 524288, and the dimension of
a square matrix n = SQRT (524288) = 724.
Fragment
of the program for calculating the multiplication matrix:
// Addresses of the
arrays
#define aa
0xD0100000
#define bb
0xD0300000
#define
cc 0xD0500000
// Cleaning SDRAM
memory 0xD0100000 - 0xD0700000 address
for(int
ie=0xD0100000;ie<=0xD0700000;ie++) *(uint32_t*)
(ie)=0x00;
// The allocation
of the array a in the memory SRAM
a = (float
*)calloc(n1, sizeof(float));
// Matrix
multiplication according to the first embodiment
for(im=1;im<=nn;im++) { for(jm=1;jm<=nn;jm++)
{ *(float*) (aa +4*(im+(jm-1)*nn))
=1.0f*((float)(im*jm));
*(float*) (bb +4*(im+(jm-1)*nn))=1.0f/(*(float*) (aa
+4*(im+(jm-1)*nn)));
*(float*) (cc +4*(im+(jm-1)*nn))=0.0f;
}
}
// Matrix
multiplication according to the second embodiment
// Here
you enter the one-dimensional array a[]
// This increases
performance for large matrices
for(im=1;im<=nn;im++) {
for(int m2=1;m2<=nn;m2++) a[m2]=*(float*) (aa +4*(im+(m2-1)*nn));
for(jm=1;jm<=nn;jm++) { *(float*) (cc +4*(im+(jm-1)*nn))=0.0f;
for(k=1;k<=nn;k++)
*(float*) (cc
+4*(im+(jm-1)*nn))=*(float*) (cc +4*(im+(jm-1)*nn))
+a[k]*(*(float*)
(bb +4*(k+(jm-1)*nn)));
} }
Before
compile we increase the size HEAP with 0x200 (512 Bytes) to 0x2F000 (192521
Bytes). It is necessary to obtain access to the entire SRAM of the
microcontroller. We are creating an intermediate array for accelerating
matrix multiplication in the SRAM (Figure 3).
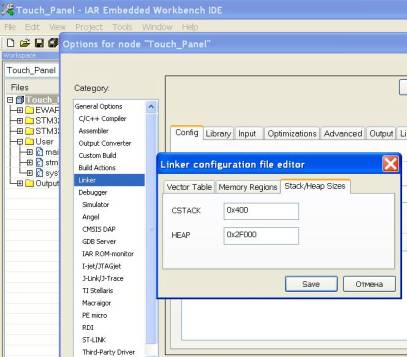
Fig.3. Increase HEAP to 0x2F00
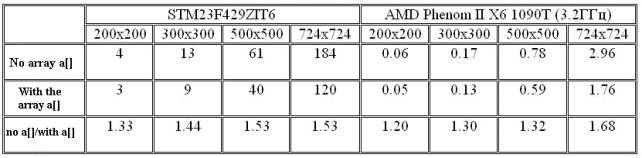
Table
1 presents the calculation results of the multiplication of square matrices for
the microcontroller. The computation time is given in seconds. Shows the
results of solving this problem on a computer with CPU AMD Phenom II X6 1090T
(3.2 GHz).
Table 1
Conclusions
1. PC based on AMD Phenom II X6
1090T (3.2GHz) operates on the matrix operations in approximately 70 times
faster microcontroller with memory SDRAM. If you compile your computer to
perform key optimization -O2, the computer will run about 255 times faster than
the microcontroller.
2. The computational speed increases 1.5 - 1.6 times with the introduction of the linear array a[]. This fact is true for microcontroller and PC. Therefore microcontroller effectively uses its cache memory.
3. Use SDRAM instead of SRAM reduces
performance microcontroller system is about 3.5-4 times.
References
1. 32F429IDISCOVERY. Discovery kit with STM32F429ZI MCU. [Electronic resource]. - Mode of access: http://www.st.com/web/catalog/tools/FM116/SC959/SS1532/PF259090,
2013
2. Ìÿñèùåâ À.À. Âû÷èñëèòåëüíûå âîçìîæíîñòè ïëàòû
STM32F429I-DISCO äëÿ ìàòðè÷íîãî óìíîæåíèÿ. [Electronic resource]. - Mode of access: http://webstm32.sytes.net/stm32_web/stm32_4.html.
2014.
3. 2. Ìÿñèùåâ À.À. Âû÷èñëèòåëüíûå
âîçìîæíîñòè STM32.
Ïðàêòèêà äëÿ ñòóäåíòîâ. [Electronic resource]. - Mode of access:
https://sites.google.com/site/webstm32/stm32_1. 2014.