Математика/1.Дифференциальные
и интегральные уравнения
Д.ф.-м.н. Городецький В.В., к.ф.-м.н. Мартинюк О. В.
Чернівецький
національний університет імені Юрія Федьковича,Україна
Нелокальна багатоточкова
задача для одного класу еволюційних рівнянь вищого порядку за часовою змінною
1. Вступ. Теорія
нелокальних крайових задач як розділ загальної теорії крайових задач для
рівнянь з частинними похідними інтенсивно розвивається з сімдесятих років
минулого століття. Нелокальними крайовими задачами прийнято називати задачі, в
яких замість задання значень розв’язку або його похідних на фіксованій частині
межі задається зв'язок цих значень із значеннями тих самих функцій на інших
внутрішніх або межевих многовидах. Загальне означення нелокальних умов та їх
класифікація були запроваджені А.М.Нахушевим [1].
Дослідження таких задач зумовлене
багатьма застосуваннями у механіці, фізиці, хімії, біології, екології та інших
природничо-наукових дисциплінах, які виникають при математичному моделюванні
тих чи інших процесів [2-7]. На доцільність використання нелокальних умов з
точки зору загальної теорії крайових задач вперше вказав О.О.Дезін [8], який
досліджував розв’язні розширення диференціальних операторів, породжених
загальною диференціальною операцією зі сталими коефіцієнтами. Він показав, що
для постановки коректної крайової задачі необхідно використовувати поряд з
локальними і нелокальні умови. Напрям досліджень, який розпочав О.О. Дезін,
розвивався також у працях В.К. Романка [9], М.Ю. Юнусова [10], А.Х. Мамяна
[11], О.А. Макарова [12] та ін.
Нелокальні крайові задачі у різних аспектах вивчали багато математиків,
використовуючи при цьому різні методи й підходи [9-17]. Одержані важливі
результати щодо постановки, коректної розв'язності та побудови розв'язків,
досліджені питання залежності характеру розв'язності задач від поведінки
символів операцій, сформульовані умови регулярності та нерегулярності крайових
умов для важливих випадків диференціально-операторних рівнянь. До таких задач
відноситься і нелокальна багатоточкова за часом задача, яка є узагальненням
задачі Коші, коли початкова умова ![]() замінюється умовою
замінюється умовою
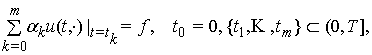 (1)
(1)
![]() ,
, ![]() , – фіксовані числа (якщо
, – фіксовані числа (якщо ![]() ,
, ![]() , то маємо, очевидно, задачу Коші).
, то маємо, очевидно, задачу Коші).
У даній роботі досліджується нелокальна багатоточкова задача з умовою
(1) для диференціально-операторного рівняння ![]() -го порядку за часовою змінною (
-го порядку за часовою змінною (![]()
![]() ) з невід'ємним самоспряженим оператором у гільбертовому
просторі з суто дискретним спектром. Позитивні та негативні простори, які
відповідають такому оператору, включаються в простір формальних рядів Фур'є, що
ототожнюються з певними лінійними неперервними функціоналами (узагальненими
елементами). У просторі формальних рядів Фур'є визначається абстрактна операція
згортки, за допомогою якої вказані оператори трактуються як оператори згортки.
На підставі такого підходу встановлюється розв'язність нелокальної
багатоточкової задачі, при цьому будується фундаментальний розв'язок (ФР)
) з невід'ємним самоспряженим оператором у гільбертовому
просторі з суто дискретним спектром. Позитивні та негативні простори, які
відповідають такому оператору, включаються в простір формальних рядів Фур'є, що
ототожнюються з певними лінійними неперервними функціоналами (узагальненими
елементами). У просторі формальних рядів Фур'є визначається абстрактна операція
згортки, за допомогою якої вказані оператори трактуються як оператори згортки.
На підставі такого підходу встановлюється розв'язність нелокальної
багатоточкової задачі, при цьому будується фундаментальний розв'язок (ФР) ![]() ,
, ![]() , досліджуються його структура та властивості. Розв'язок
, досліджуються його структура та властивості. Розв'язок ![]() подається у вигляді
згортки
подається у вигляді
згортки ![]() , де
, де ![]() – лінійний
неперервний функціонал на певному підпросторі
– лінійний
неперервний функціонал на певному підпросторі ![]() основних елементів (
основних елементів (![]() ,
, ![]() – гільбертів простір,
– гільбертів простір,
![]() – простір,
топологічно спряжений з
– простір,
топологічно спряжений з ![]() ). Зазначимо, що
). Зазначимо, що ![]() ,
, ![]() при кожному
при кожному ![]() , але умову (1)
, але умову (1) ![]() задовольняє в
слабкому сенсі, тобто
задовольняє в
слабкому сенсі, тобто 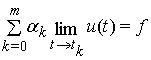 ,
, ![]() , де границі розглядаються в просторі
, де границі розглядаються в просторі ![]() , який є ''максимальним'' простором елементів (лінійних
неперервних функціоналів) для постановки нелокальної багатоточкової задачі,
розв'язок якої володіє характерними властивостями ФР такої задачі.
, який є ''максимальним'' простором елементів (лінійних
неперервних функціоналів) для постановки нелокальної багатоточкової задачі,
розв'язок якої володіє характерними властивостями ФР такої задачі.
2. Формальні ряди Фур'є. Нехай ![]() – невід'ємний
самоспряжений оператор з дискретним спектром в сепарабельному гільбертовому
просторі
– невід'ємний
самоспряжений оператор з дискретним спектром в сепарабельному гільбертовому
просторі ![]() зі скалярним добутком
зі скалярним добутком
![]() та нормою
та нормою ![]() ,
, ![]() – область визначення
оператора
– область визначення
оператора ![]() , щільна в
, щільна в ![]() ,
, ![]() – ортонормований базис в
– ортонормований базис в ![]() із його власних
векторів,
із його власних
векторів, ![]() – монотонно зростаюча
послідовність відповідних власних чисел,
– монотонно зростаюча
послідовність відповідних власних чисел, ![]() ,
, ![]() , при цьому виконується умова:
, при цьому виконується умова: 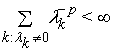 при деякому
при деякому ![]() . Введемо позначення:
. Введемо позначення:
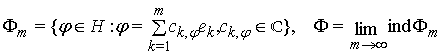 (
(![]() лежить щільно в
лежить щільно в ![]() і є інваріантним
відносно оператора
і є інваріантним
відносно оператора ![]() ),
), ![]() – простір всіх
антилінійних неперервних функціоналів на
– простір всіх
антилінійних неперервних функціоналів на ![]() зі слабкою збіжністю:
зі слабкою збіжністю:
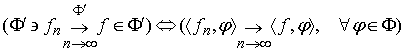
(символ над стрілкою позначає простір, в якому
розглядається збіжність, ![]() – дію функціоналу
– дію функціоналу ![]() на елемент
на елемент ![]() ).
).
Зіставлення ![]()
визначає вкладення ![]() . Отже,
. Отже, ![]() , причому вкладення щільні і неперервні. Елементи з
, причому вкладення щільні і неперервні. Елементи з ![]() називатимемо
узагальненими.
називатимемо
узагальненими.
Нехай ![]() – простір усіх
числових послідовностей
– простір усіх
числових послідовностей ![]() ,
, ![]() , з покоординатною збіжністю. Ізоморфізм
, з покоординатною збіжністю. Ізоморфізм ![]() з
з ![]() на
на ![]() відображає
відображає ![]() на множину фінітних
послідовностей з
на множину фінітних
послідовностей з ![]() , а
, а ![]() – на
– на ![]() . При цьому оператору
. При цьому оператору ![]() відповідає операція
відповідає операція ![]() і його можна
продовжити на
і його можна
продовжити на ![]() до неперервного
оператора
до неперервного
оператора ![]() :
: ![]() ,
, 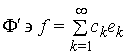 [18]. Нехай
[18]. Нехай ![]() . Ряд
. Ряд 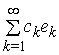 , де
, де ![]() , називається рядом Фур'є елемента
, називається рядом Фур'є елемента ![]() , а числа
, а числа ![]() – його коефіцієнтами
Фур'є. Для довільного елемента
– його коефіцієнтами
Фур'є. Для довільного елемента ![]() його ряд Фур'є
збігається в
його ряд Фур'є
збігається в ![]() до
до ![]() і навпаки, довільний
ряд
і навпаки, довільний
ряд 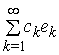 збігається в
збігається в ![]() до деякого елемента
до деякого елемента ![]() і цей ряд є рядом
Фур'є для
і цей ряд є рядом
Фур'є для ![]() [18]. Отже,
[18]. Отже, ![]() можна розуміти як простір
формальних рядів вигляду
можна розуміти як простір
формальних рядів вигляду 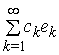 .
.
Введемо деякі класи елементів, пов'язані з оператором ![]() . Для цього розглянемо монотонно зростаючу послідовність
. Для цього розглянемо монотонно зростаючу послідовність ![]() ,
, ![]() , додатних чисел, яка володіє властивостями [18]: 1)
, додатних чисел, яка володіє властивостями [18]: 1) ![]()
![]()
![]() :
: ![]() ; 2)
; 2) ![]()
![]()
![]() :
: ![]() .
.
Прикладами таких послідовностей є послідовності Жевре вигляду ![]() ,
, ![]() ,
, ![]() , де
, де ![]() – фіксований
параметр. Позначимо
– фіксований
параметр. Позначимо ![]()
![]()
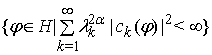 ,
,
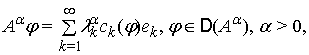
![]()
Простір ![]() – банаховий відносно
норми
– банаховий відносно
норми 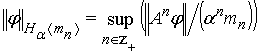 . Покладемо
. Покладемо ![]() . Тоді
. Тоді ![]() , причому всі вкладення є щільними і неперервними [18]. Якщо
через
, причому всі вкладення є щільними і неперервними [18]. Якщо
через ![]() ,
, ![]() позначити простори
антилінійних неперервних функціоналів на
позначити простори
антилінійних неперервних функціоналів на ![]() ,
, ![]() відповідно, то,
згідно з [18], прийдемо до ланцюжка щільних і неперервних вкладень
відповідно, то,
згідно з [18], прийдемо до ланцюжка щільних і неперервних вкладень ![]() ; при цьому
; при цьому ![]() .
.
Нехай 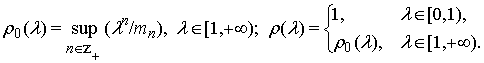
Із властивостей послідовності ![]() випливає, що функція
випливає, що функція ![]() неперервна на
неперервна на ![]() , монотонно зростає на
, монотонно зростає на ![]() швидше за довільний
степінь
швидше за довільний
степінь ![]() [18]. З точки зору поведінки коефіцієнтів Фур'є
їхніх елементів простори
[18]. З точки зору поведінки коефіцієнтів Фур'є
їхніх елементів простори ![]() та
та ![]() описуються так [18]:
описуються так [18]:
![]()
![]()
Простори ![]() ,
, ![]() , називаються просторами Жевре порядку
, називаються просторами Жевре порядку ![]() , породженими оператором
, породженими оператором ![]() ;
; ![]() збігається з множиною
аналітичних векторів оператора
збігається з множиною
аналітичних векторів оператора ![]() [18]. Якщо
[18]. Якщо ![]() ,
, ![]() , то
, то ![]() ~
~![]() ,
, ![]() , тобто в цьому випадку для
, тобто в цьому випадку для ![]() правильними є
співвідношення еквівалентності:
правильними є
співвідношення еквівалентності:
![]()
![]()
3. Невід'ємні самоспряжені оператори як оператори
згортки. Нехай ![]() ,
, 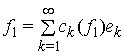 ,
, 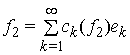 . У просторі
. У просторі ![]() визначимо операцію ''*'',
яку назвемо ''абстрактною згорткою'', або просто згорткою, за правилом
визначимо операцію ''*'',
яку назвемо ''абстрактною згорткою'', або просто згорткою, за правилом 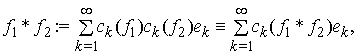
тобто ![]() – узагальнений
елемент з простору
– узагальнений
елемент з простору ![]() , коефіцієнти Фур'є якого пов'язані з коефіцієнтами Фур'є
узагальнених елементів
, коефіцієнти Фур'є якого пов'язані з коефіцієнтами Фур'є
узагальнених елементів ![]() ,
, ![]() співвідношенням
співвідношенням ![]() ,
, ![]() .
.
Розглянемо послідовність ![]() , за якою будуються простори
, за якою будуються простори ![]() та
та ![]() , спеціального вигляду, а саме,
, спеціального вигляду, а саме, ![]() , де
, де ![]() ,
, ![]() , – послідовність додатних чисел, яка: а) монотонно спадна;
б)
, – послідовність додатних чисел, яка: а) монотонно спадна;
б) ![]()
![]() :
: ![]() ; в)
; в) ![]() . Послідовність
. Послідовність ![]() , як встановлено в [19], володіє властивостями 1), 2).
Прикладом послідовності
, як встановлено в [19], володіє властивостями 1), 2).
Прикладом послідовності ![]() з властивостями а) –
в) може служити послідовність
з властивостями а) –
в) може служити послідовність ![]() ,
, ![]() , де
, де ![]() – фіксований параметр
[19].
– фіксований параметр
[19].
Якщо ![]() , то функція
, то функція ![]() , побудована за такою послідовністю, диференційовна на
, побудована за такою послідовністю, диференційовна на ![]() [19], при цьому справджується
нерівність
[19], при цьому справджується
нерівність
![]() .
.
Зауважимо також, що послідовність ![]() задовольняє умову
задовольняє умову ![]() , з якої випливає (див. [20]), що
, з якої випливає (див. [20]), що ![]() ,
, ![]() , з деякими сталими
, з деякими сталими ![]() ,
, ![]() . Правильним є таке твердження.
. Правильним є таке твердження.
Лема 1. а) Якщо ![]() , то
, то ![]() .
.
б) Для довільних ![]() та
та ![]() згортка
згортка ![]() є елементом простору
є елементом простору ![]() .
.
Нехай ![]() :
: ![]() – неперервна функція,
монотонно зростаюча на
– неперервна функція,
монотонно зростаюча на ![]() ,
, ![]() . За функцією
. За функцією ![]() та оператором
та оператором ![]() побудуємо оператор
побудуємо оператор ![]() :
:
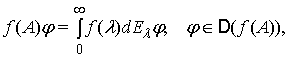 (2)
(2)
де ![]() ,
, ![]() , – спектральна функція оператора
, – спектральна функція оператора ![]() , з областю визначення
, з областю визначення
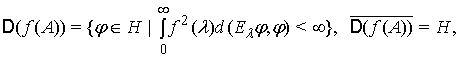 який також є
невід'ємним і самопряженим в
який також є
невід'ємним і самопряженим в ![]() . Інтеграл (2) береться, фактично, лише по спектру
. Інтеграл (2) береться, фактично, лише по спектру ![]() оператора
оператора ![]() , який, у даному випадку, є дискретним з єдиною граничною
точкою у нескінченності:
, який, у даному випадку, є дискретним з єдиною граничною
точкою у нескінченності: ![]() . Спектральна функція
. Спектральна функція ![]() ,
, ![]() , – кусково-стала і має розриви лише в точках
, – кусково-стала і має розриви лише в точках ![]() ,
, ![]() , причому
, причому ![]() – оператор
проектування на власний підпростір оператора
– оператор
проектування на власний підпростір оператора ![]() , що відповідає власному значенню
, що відповідає власному значенню ![]() . Відповідні власні вектори
. Відповідні власні вектори ![]() ,
, ![]() , утворюють ортонормований базис в
, утворюють ортонормований базис в ![]() , тому
, тому ![]() ,
, ![]() . Тут
. Тут ![]() ,
, ![]() , у цьому випадку має вигляд
, у цьому випадку має вигляд ![]() ,
, ![]() , а інтеграл (2)
є таким:
, а інтеграл (2)
є таким: 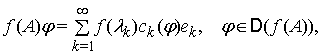
![]() ,
, ![]() , – власні значення оператора
, – власні значення оператора ![]() . Продовжимо
. Продовжимо ![]() на
на ![]() до неперервного
оператора
до неперервного
оператора ![]() :
: 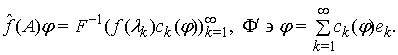
Розглянемо узагальнений елемент 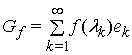 з простору
з простору ![]() , побудований за функцією
, побудований за функцією ![]() . Тоді
. Тоді ![]() – оператор згортки,
який діє у просторі
– оператор згортки,
який діє у просторі ![]() за правилом:
за правилом: 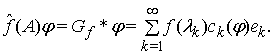 Оператор
Оператор ![]() розумітимемо як
звуження оператора
розумітимемо як
звуження оператора ![]() на
на ![]() .
.
Лема 2. Оператор ![]() неперервний у
просторі
неперервний у
просторі ![]() тоді і лише тоді,
коли
тоді і лише тоді,
коли ![]() .
.
Зауваження 1. Умова ![]() еквівалентна такій
умові на функцію
еквівалентна такій
умові на функцію ![]() :
: ![]()
4. Нелокальна
багатоточкова задача. Розглянемо диференціально-операторне рівняння
![]() (3)
(3)
де ![]() – оператор,
побудований у п. 3, який є лінійним і неперервним у просторі
– оператор,
побудований у п. 3, який є лінійним і неперервним у просторі ![]() ,
, ![]()
![]() – фіксоване. Надалі
вважаємо, що функція
– фіксоване. Надалі
вважаємо, що функція ![]() задовольняє умову:
задовольняє умову: ![]()
Під розв'язком рівняння (3) розуміємо функцію ![]() :
: ![]() , двічі сильно диференнційовну в
, двічі сильно диференнційовну в ![]() , яка задовольняє рівняння (3).
, яка задовольняє рівняння (3).
Теорема 1. Для довільного 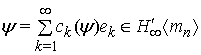 функція
функція
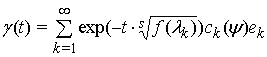 (4)
(4)
є розв'язком рівняння (3).
Зауваження 2. Введемо
позначення 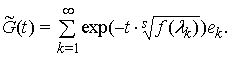
Із властивостей функції ![]() випливає, що
випливає, що ![]() при кожному
при кожному ![]() . Крім того,
. Крім того, ![]() ,
, ![]() . Отже, оператор згортки
. Отже, оператор згортки ![]() переводить кожний
елемент простору
переводить кожний
елемент простору ![]() (зокрема, кожний
елемент простору
(зокрема, кожний
елемент простору ![]() ) у розв'язок рівняння (3).
) у розв'язок рівняння (3).
Поставимо задачу: в множині
розв'язків рівняння (3) вигляду (4) знайти розв'язок, який задовольняє умову
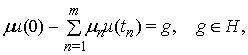 (5)
(5)
![]() ,
, ![]() ,
, ![]() , – фіксовані числа,
, – фіксовані числа, 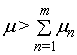 ,
, ![]() ; при цьому
; при цьому ![]() розуміємо як
розуміємо як ![]() , де границя розглядається в просторі
, де границя розглядається в просторі ![]() (тобто вважаємо, що
існує елемент
(тобто вважаємо, що
існує елемент ![]() такий, що
такий, що ![]() ,
, ![]() ;
; ![]() ). Вказану задачу називатимемо багатоточковою задачею для
рівняння (3). Із теореми 1 та зауваження 2 випливає, що задачу (3), (5) можна
ставити ще й так: у класі
). Вказану задачу називатимемо багатоточковою задачею для
рівняння (3). Із теореми 1 та зауваження 2 випливає, що задачу (3), (5) можна
ставити ще й так: у класі ![]() знайти елемент
знайти елемент ![]() , який у згортці з
, який у згортці з ![]() дає розв'язок
рівняння (3), що задовольняє умову (5) (у вказаному розумінні). Відповідь на
поставлене питання дає наступна теорема.
дає розв'язок
рівняння (3), що задовольняє умову (5) (у вказаному розумінні). Відповідь на
поставлене питання дає наступна теорема.
Теорема
2. Задача (3), (5) розв'язна, розв'язок дається формулою
![]() , де
, де ![]() ,
, 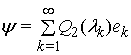 ,
, ![]()
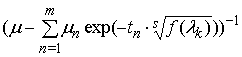 , причому
, причому ![]() ,
, ![]() .
.
Із леми 1 випливає, що згортку ![]() можна розглядати і у
випадку, коли
можна розглядати і у
випадку, коли ![]() , при цьому
, при цьому ![]() при кожному
при кожному ![]() .
.
Для рівняння (3) задамо умову вигляду (5) з елементом ![]() ; при цьому під
розв'язком відповідної багатоточкової задачі розуміємо функцію
; при цьому під
розв'язком відповідної багатоточкової задачі розуміємо функцію ![]() , яка є розв'язком
рівняння (3), а (5) задовольняє в сенсі:
, яка є розв'язком
рівняння (3), а (5) задовольняє в сенсі:
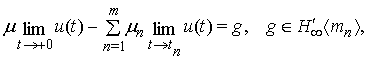 (6)
(6)
де границі
в (6) розглядаються в просторі ![]() .
.
Теорема 3. Багатоточкова
задача (3), (6) розв'язна, розв'язок має вигляд ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Як приклад, розглянемо самоспряжений оператор ![]() , породжений у гільбертовому просторі
, породжений у гільбертовому просторі ![]() диференціальним
виразом
диференціальним
виразом ![]() та умовами
та умовами ![]() ,
, ![]() ,
, ![]() – модуль оператора
диференціювання,
– модуль оператора
диференціювання, ![]() . Спектр оператора
. Спектр оператора ![]() – дискретний:
– дискретний: ![]() з єдиною граничною
точкою у нескінченності,
з єдиною граничною
точкою у нескінченності, ![]() ,
, ![]() ,
, ![]() , – його власні функції. У цьому випадку
, – його власні функції. У цьому випадку
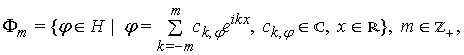
тобто кожний елемент з ![]() є тригонометричним
поліномом степеня
є тригонометричним
поліномом степеня ![]() ,
, ![]() – простір усіх
формальних тригонометричних рядів, які ототожнюються з узагальненими
– простір усіх
формальних тригонометричних рядів, які ототожнюються з узагальненими ![]() -періодичними функціями як антилінійнийними неперервними
функціоналами на просторі тригонометричних ноліномів [21].
-періодичними функціями як антилінійнийними неперервними
функціоналами на просторі тригонометричних ноліномів [21].
Згортка двох узагальнених періодичних функцій ![]() визначається так
[21]:
визначається так
[21]: ![]() ,
, ![]() . Вона має
зміст, бо
. Вона має
зміст, бо 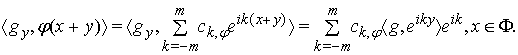
При відображенні ![]() простір
простір ![]() відображається на
відображається на ![]() , оператор
, оператор ![]() переходить у оператор
множення на
переходить у оператор
множення на ![]() , згортка – в покоординатне множення:
, згортка – в покоординатне множення: ![]()
![]()
![]() ,
, ![]() . Отже,
. Отже, ![]() – узагальнена
– узагальнена ![]() періодична функція з
періодична функція з ![]() , яка ототожнюється з рядом Фур'є
, яка ототожнюється з рядом Фур'є 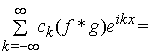
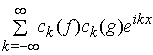 , а згортка в
, а згортка в ![]() збігається з
''абстрактною згорткою'', введеною в п. 3.
збігається з
''абстрактною згорткою'', введеною в п. 3.
За послідовність ![]() візьмемо
послідовність
візьмемо
послідовність ![]() , де
, де ![]() – фіксований
параметр. Як зазначалося раніше, послідовність
– фіксований
параметр. Як зазначалося раніше, послідовність ![]() задовольняє умови а)
– в), відповідна послідовність
задовольняє умови а)
– в), відповідна послідовність ![]() володіє властивостями
1), 2),
володіє властивостями
1), 2), ![]() ~
~![]() ,
, ![]() . За функцію
. За функцію ![]() , за допомогою якої будується оператор
, за допомогою якої будується оператор ![]() , візьмемо
, візьмемо ![]() ,
, ![]() . Безпосередньо переконуємося в тому, що при виконанні умов
. Безпосередньо переконуємося в тому, що при виконанні умов ![]() ,
, ![]() , функція
, функція ![]() задовольняє відповідні
умови. Наприклад, якщо взяти
задовольняє відповідні
умови. Наприклад, якщо взяти ![]() , то
, то ![]() ,
, ![]() ; при цьому рівняння (3) при
; при цьому рівняння (3) при ![]() набуває вигляду
набуває вигляду
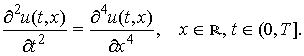 (7)
(7)
Нелокальна багатоточкова задача для рівняння (7) з умовою (6), де ![]() , розв'язна (у вказаному раніше сенсі: відповідні границі в
(6) розглядаються в просторі
, розв'язна (у вказаному раніше сенсі: відповідні границі в
(6) розглядаються в просторі ![]() ). Розв'язком є
). Розв'язком є ![]() -періодична і нескінченно диференційовна за змінною
-періодична і нескінченно диференційовна за змінною ![]() функція
функція
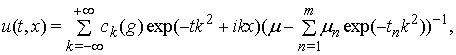
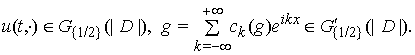
Отже, узагальнені ![]() -періодичні функції з простору
-періодичні функції з простору ![]() можна брати за
функції, за допомогою яких ставиться нелокальна умова (6), при цьому розв'язок
можна брати за
функції, за допомогою яких ставиться нелокальна умова (6), при цьому розв'язок ![]() відповідної задачі
зберігає властивості гладкого розв'язку ''класичної'' нелокальної задачі для
рівняння (7) з умовою (5), де
відповідної задачі
зберігає властивості гладкого розв'язку ''класичної'' нелокальної задачі для
рівняння (7) з умовою (5), де ![]() .
.
Література:
1.
Нахушев А.М., Об
одном приближенном методе решения краевых задач для дифференциальных уравнений
и его приложения к динамике почвенной влаги и грунтовых вод, Дифференц.
уравнения. 18 (N 1) (1982), 77-81.
2.
Майков А.Р.,
Поезд А.Д., Якунин С.А., Экономический метод вычисления нестационарных
нелокальных по времени условий излучения для волновых систем, Журн.
вычислит. математики и мат. физики. 30 (N 8) (1990), 1267-1271.
3.
Нахушев А.М., Уравнения
математической биологии, Высшая школа, Москва, 1995.
4. Белавин И.А., Капица С.П., Курдюмов С.П.,
Математическая модель глобальных демографических процессов с учетом
пространственного распределения, Журн. вычислит. математики и мат. физики.
38 (N 6) (1988), 885-902.
5. Bouzinab A., Arino
O., On the existence and uniqueness for an age-depent population model with
nonlinear growth, Facta Univ. Ser. Math Inf. 8 (1993), 55-68.
6. Cannon I.R., J. van
der Hoek, Diffusion subject to the specification of mass, J. Math. Anal. and
Appl. 115 (N 2) (1986), 517-529.
7.
Song J., Some developments in mathematical demography and their
applicatioto the Peoples Republic of China, Theor Pop. Biol. 22 (N 3) (1982), 382-391.
8.
Дезин А.А.,
Операторы с первой производной по ''времени'' и нелокальные граничные условия, Изв.
АН СССР. Сер. мат. 31 (N 1) (1967), 61-86.
9.
Романко В.К.,
Граничные задачи для одного класса дифференциальных операторов, Дифференц.
уравнения. 10 (N 1) (1974), 117-131.
10.
Юнусов М.Ю.,
Операторные уравнения с малым параметром и нелокальные граничные условия, Дифференц.
уравнения. 17 (N 1) (1981), 172-181.
11.
Мамян А.Х.,
Общие граничные задачи в слое, ДАН СССР. 267 (N 2) (1982), 292-296.
12.
Макаров А.А.,
Существование корректной двухточечной краевой задачи в слое для систем
псевдодифференциальных уравнений, Дифференц. уравнения. 30 (N 1)
(1994), 144-150.
13.
Нахушев А.М., О
нелокальных краевых задачах со смещением и их связи с нагруженными уравнениями,
Дифференц. уравнения. 21 (N 1) (1985), 92-101.
14.
Самарский А.А.,
О некоторых проблемах теории дифференциальных уравнений, Дифференц.
уравнения. 16 (N 11) (1980), 1925-1935.
15.
Пташник Б.Й.,
Ільків В.С., Кміть І.Я., Поліщук В.М., Нелокальні крайові задачі для рівнянь
з частинними похідними, Наук. думка, Київ, 2002.
16.
Чесалин В.И.,
Задача с нелокальными граничными условиями для некоторых абстрактных
гиперболических уравнений, Дифференц. уравнения. 15 (N 11)
(1976), 2104-2106.
17.
Скубачевский
А.Л., Модельные нелокальные задачи для эллиптических уравнений в двугранных
углах, Дифференц. уравнения. 26 (N 1) (1990), 120-131.
18.
Горбачук В.И., О
разрешимости задачи Дирихле для дифференциально-операторного уравнения второго
порядка в различных пространствах, Прямые и обратные задачи спектральной
теории дифференциальных операторов: Сб. науч. трудов., Киев, 1985.
19.
Городецький
В.В., Задача Коші для еволюційних рівнянь нескінченного порядку, Рута,
Чернівці, 2005.
20.
Бабенко К.И., Об
одной новой проблеме квазианалитичности и о преобразовании Фурье для целых
функций, Труды Моск. матем. общества. 5 (1956), 523-542.
21.
Горбачук В.И.,
Горбачук М.Л., Граничные значения решений дифференциально-операторных
уравнений, Наук. думка, Киев, 1984.