Доктор физ.-мат. наук, доц.
А.В. Макаричев, А. А. Кудь, А.Б.Щукин
Национальный аэрокосмический
университет «ХАИ»
Харьковский национальный автомобильно-дорожный университет
Московский государственный университет им. М.В.
Ломоносова
ПРОСТЕЙШАЯ ИНВАРИАНТНАЯ ДИСЦИПЛИНА
ОБСЛУЖИВАНИЯ В МНОГОЛИНЕЙНОЙ СИСТЕМЕ МАССОВОГО ОБСЛУЖИВАНИЯ
Совершенствование
электронно-вычислительной техники выдвигает актуальное направление исследований
- поиск рационального числа обслуживающих приборов в многолинейной системе
массового обслуживания. При этом встает проблема обеспечения рационального
обслуживания в случае тяжелых «хвостов» распределения длины (времени
обслуживания со скоростью единица) требований. Эта проблема возникает, когда
старшие моменты, начиная со второго, времени обслуживания требований, вообще
говоря, могут быть бесконечными. Предлагается определенный характер
обслуживания для преодоления этой трудности.
Рассмотрим
многолинейную систему массового обслуживания, состоящую из 
обслуживающих
приборов с входящим пуассоновским простейшим потоком требований с параметром 
и функцией
распределения длины требования 
. Приведем описание дисциплины обслуживания. Если в системе
массового обслуживания есть хотя бы два свободных прибора, поступающее
требование занимает свободный обслуживающий прибор и обслуживается на нем со
скоростью единица. Если же поступающее в систему требование застает в ней ровно
один обслуживающий прибор, то работа по его обслуживанию делится на 
равных частей. Они
занимают все 
обслуживающих
приборов (ровно по одной части на прибор), а не до конца обслуженные требования становятся в очередь и затем
завершают обслуживание при освобождении одновременно всех 
приборов. Если при
обслуживании разделенного на части требования в систему массового обслуживания
поступает еще одно требование, то работа по его обслуживанию также делится на 
равных частей, и они
занимают все 
приборов, отправляя
первым в очередь 
частей требования,
перед этим не до конца обслуженного этими приборами. При окончании обслуживания 
равных частей
требования приборы начинают дообслуживание 
равных частей
разделенного на части требования, стоящего первым в очереди. А если таких
требований нет, то начинают дообслуживание те 
требований, которые были
отправлены в очередь ранее. И так далее.
Обозначим 
математическое ожидание длины требования,
нагрузку на систему массового обслуживания. Через 
, обозначим общее число требований в системе массового
обслуживания (находящихся на обслуживании и, быть может, в очереди). Оставшуюся
длину дообслуживания 
го требования
(нумерация идет от единицы в порядке поступления – меньший номер у ранее
пришедшего требования). Случайный процесс 
показывает состояние процесса обслуживания в
многолинейной системе в момент времени 
. Обозначим 
,
, 
.
Вероятности 
того, что в системе
массового обслуживания в момент 
находятся ровно 
требований,
определяются по формулам:
при 
,
при 
,
а соответствующие стационарные вероятности существуют
когда 
[1] и равны 
,
, 
,
.
Следуя нашим великим учителям [1-5], составим дифференциальные
уравнения Колмогорова для стационарных вероятностей состояний случайного
процесса 
при 
,
, при 
при 
.
Составим так же уравнения Колмогорова в частных
производных для стационарных вероятностей состояний случайного процесса
и для 
.
Группируя равные слагаемые в уравнениях, представим
решение данной бесконечной системы дифференциальных уравнений в частных
производных для стационарных вероятностей состояний случайного процесса в виде
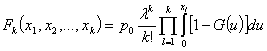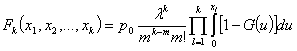, при 
, при 
, где
,
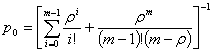в чем можно убедиться,
непосредственно подставляя его в дифференциальные уравнения. Отсюда при 
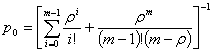
при 
и
при 
.
Заметим, что при таком характере обслуживания
требований в многолинейной системе стационарные вероятности состояний случайного
процесса числа требований в системе при фиксированном математическом ожидании времени
обслуживания требований не зависят от вида его функции распределения.
Литература
1. B. V. GNEDENKO AND
I. N. KOVALENKO, Introduction to Queueing
Theory, Program for Scientific Translations, Jerusalem, 1968.
2.
Вопросы математической теории надежности /Е.Ю.
Барзилович, Ю.К. Беляев, В.А. Каштанов, И.Н. Коваленко,
А.Д. Соловьев, И.А. Ушаков; Под ред. Б. В. Гнеденко.- М.:
Радио и связь, 1983.- 376 с., ил.
3.
Б.А. Севастьянов.
Эргодическая теорема для Марковских
процессов и ее приложения к телефонным системам с
отказами. Теория вероятностей и ее применения, т. 2, вып. 1,
1957, 106-116.
4. А.Н. Ширяев. Вероятность, М.: Наука,
1980, 576 c.
5. R. Fortet. Theorie des probabilities,
Centre Nat. Rech. Scient.,
Paris, 1950.