Математика/4. Прикладная математика
Д.т.н.
Федотов А.И., к.т.н. Лисин С.К.
СПб политехнический университет Петра
Великого, РОССИЯ
СПб
национальный минерально-сырьевой университет «Горный», РОССИЯ
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ВИБРАЦИОННО-
КОНТАКТНОГО КОНТРОЛЯ C ИСПОЛЬЗОВАНИЕМ
ВИБРИРУЮЩИХ ПРЕОБРАЗОВАТЕЛЕЙ
Создание и развитие вибрационных, виброударных
и других методов измерений и контроля параметров и свойств изделий, в том числе
контроля свойств объектов замкнутого технологического цикла, связано с
необходимостью построения адекватных теоретических моделей их режимов. Становятся
актуальными задачи прогнозирования и анализа нелинейных динамических режимов [1-3,6,7],
имеющих важнейшее значение в мировой практике для повышения точности и
эффективности методов и средств контроля удара, вибрации и обеспечения вибро-защиты.
Рассмотрим математические модели колебаний подобных
подвижных систем в режиме вибрационного контакта измерительного наконечника преобразователя
с объектом контроля. При этом нелинейные численно решаемые математические
модели будут реализованы как точными, так и асимптотическими методами. Функциональная
схема одномерного вибрационно-контактного преобразователя содержит измерительный
наконечник, соударяющегося с поверхностью контролируемого объекта. В одномерном
исполнении преобразователь [3] содержит мультивибратор и высокочувствительную генераторную
систему. Подвижная система преобразователя
имеет нелинейную динамическую
характеристику, обусловленную существенным различием жесткости упругого подвеса измерительного наконечника
в зоне и вне зоны его контакта с поверхностью контролируемого изделия. Резонансный
режим измерительного наконечника поддерживается мультивибратором
преобразователя.
Восстанавливающая характеристика ![]() в
интервалах упругой характеристики выражается двумя различными функциями и не
является линейной функцией. Подобные функции, составленные из линеаризованных отрезков
и остающиеся однозначными в отдельном закрытом интервале, получили название
кусочно-линейных функций. При этом выражения
упругих характеристик в безразмерной форме для решений методом
«сшивания» и асимптотическим методом соответственно имеют вид:
в
интервалах упругой характеристики выражается двумя различными функциями и не
является линейной функцией. Подобные функции, составленные из линеаризованных отрезков
и остающиеся однозначными в отдельном закрытом интервале, получили название
кусочно-линейных функций. При этом выражения
упругих характеристик в безразмерной форме для решений методом
«сшивания» и асимптотическим методом соответственно имеют вид:
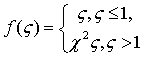 ;
; 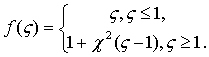
В соответствии с методом гармонического баланса (метод
Боголюбова Н.Н.) соответствующее решение записывается в виде ![]() .
.
Здесь ![]() и
и ![]() - смещение центра и амплитуда колебаний;
- смещение центра и амплитуда колебаний;![]() - относительная жесткость;
- относительная жесткость; ![]() .
Уравнение
.
Уравнение ![]() , соответствует координате системы
, соответствует координате системы ![]() = 1 и фазовому
параметру
= 1 и фазовому
параметру ![]() .
.
Следовательно, уравнение для определения смещения
центра колебаний ![]() измерительного наконечника методом гармонического баланса
принимает вид
измерительного наконечника методом гармонического баланса
принимает вид ![]() . В численно решаемую
систему
уравнений искомых переменных входит амплитуда колебаний измерительного
наконечника вибрирующего преобразователя
. В численно решаемую
систему
уравнений искомых переменных входит амплитуда колебаний измерительного
наконечника вибрирующего преобразователя
![]() вида
вида
![]()
Здесь ![]() - амплитуда возмущающего воздействия преобразователя.
- амплитуда возмущающего воздействия преобразователя.
Замкнутая
система уравнений позволяет установить
аналитическую зависимость жесткости χ2 в виде
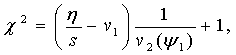 (1)
(1)
где – v1 и v2 - жесткости упругого подвеса и объекта контроля
соответственно.
Для применения метода измерения жесткости
необходимо получить зависимость жесткости χ(![]() ) с помощью численных решений системы. Смещение центра
колебаний
) с помощью численных решений системы. Смещение центра
колебаний ![]() характеризует
изменение амплитуды выходного сигнала преобразователя при изменении
физико-механических свойств контролируемых объектов.
характеризует
изменение амплитуды выходного сигнала преобразователя при изменении
физико-механических свойств контролируемых объектов.
В общем виде областью определения функции точного
решения ![]() является интервал [
является интервал [![]() ,
1]. Здесь
,
1]. Здесь ![]() – координата положения измерительного
наконечника (
– координата положения измерительного
наконечника (![]() ), отсчитываемая от равновесного положения; Δ – зазор
измерительной системы. Областью определения функций
), отсчитываемая от равновесного положения; Δ – зазор
измерительной системы. Областью определения функций ![]() и
и ![]() является интервал [1,
является интервал [1, ![]() ].
].
В варианте точного решения дифференциальное
уравнение вынужденных колебаний на интервале ![]() имеет вид
имеет вид
![]() , (2)
, (2)
где 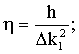
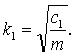
В интервале ![]() имеем
имеем
![]() . (3)
. (3)
Для определения точных периодических решений
системы уравнений (2), (3) целесообразен метод «припасовывания». Следуя методу
припасовывания, для уравнения (3) принимаем начальные условия:
![]() , (4)
, (4)
где
![]() –
момент времени, соответствующий вхождению измерительного наконечника в
контакт с поверхностью объекта
измерения. Конечные условия для уравнения (3):
–
момент времени, соответствующий вхождению измерительного наконечника в
контакт с поверхностью объекта
измерения. Конечные условия для уравнения (3):
![]() (5)
(5)
где
![]() –
момент выхода измерительного наконечника из фазы контакта.
–
момент выхода измерительного наконечника из фазы контакта.
Начальными условиями для уравнения (2),
описывающего движение в фазе без контакта, будут условия (5). Следовательно,
конечными условиями и одновременно условиями периодичности для уравнения (2)
являются условия
![]()
![]() ,
,
![]() . (6)
. (6)
Максимальные
отклонения измерительного наконечника от положения статического равновесия ![]() вправо и
вправо и ![]() влево
определяются с учетом условий
влево
определяются с учетом условий
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() . (7)
. (7)
Приведенные соотношения обеспечивают
возможность определить амплитудно-частотные характеристики системы в режиме
вибрационного контакта измерительного наконечника преобразователя. Рассматриваемая расчетная модель строится с учетом упругих
свойств измеряемого объекта ![]() .
Режиму вынужденных колебаний на фазовой плоскости соответствует замкнутая
фазовая траектория, время пробега изображающей точки которой совпадает с
периодом возмущающей силы.
.
Режиму вынужденных колебаний на фазовой плоскости соответствует замкнутая
фазовая траектория, время пробега изображающей точки которой совпадает с
периодом возмущающей силы.
На рис. 1 представлен фазовый портрет установившихся режимов
вибрационно-контактного преобразователя.
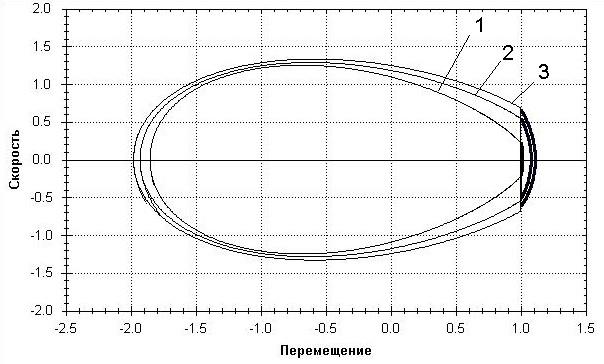
Рис. 1. Фазовая диаграмма
установившихся режимов
В табл. 1 приведены значения
параметров вибрационно-контактных режимов одномерного измерительного
преобразователя. Расчетная модель воспроизводит аналитическую связь параметра
упругих свойств измеряемого объекта с параметрами ![]() и s0 , устанавливающих
область устойчивых колебаний.
и s0 , устанавливающих
область устойчивых колебаний.
Таблица 1
|
Режимы |
|
η |
ξ |
α 2 |
α 1 |
s0 |
|
1 |
1.5 |
0.7 |
1.03 |
-1.854 |
1.013 |
0,42 |
|
2 |
1.5 |
0.7 |
1.04 |
-1.932 |
1.077 |
0,427 |
|
3 |
1.5 |
0.7 |
1.1 |
-1.96 |
1.108 |
0,426 |
Перейдем к определению
стандартной неопределенности искомой относительной жесткости системы
«измерительный наконечник – объект контроля». Жесткость χ рассматриваемой
системы является функцией параметров s0 , η, ξ, ![]() 1. При этом параметр s0 непосредственно
измеряется. Неопределенность данного параметра носит характер статистической
погрешности и определяется через
среднее квадратичное отклонение. Параметры возмущения η и частоты ξ
устанавливаются при тарировании измерительного вибрационно-контактного
преобразователя и их неопределенности являются систематическими погрешностями. Неопределенность
фазовой длительности
1. При этом параметр s0 непосредственно
измеряется. Неопределенность данного параметра носит характер статистической
погрешности и определяется через
среднее квадратичное отклонение. Параметры возмущения η и частоты ξ
устанавливаются при тарировании измерительного вибрационно-контактного
преобразователя и их неопределенности являются систематическими погрешностями. Неопределенность
фазовой длительности ![]() 1 контролируется
специальными средствами. Стандартная неопределенность типа В этой длительности вычисляется
как для случая однократного измерения с учетом погрешности, определяемой классом
точности данного средства измерений.
1 контролируется
специальными средствами. Стандартная неопределенность типа В этой длительности вычисляется
как для случая однократного измерения с учетом погрешности, определяемой классом
точности данного средства измерений.
Неопределенность χ определяется по правилу получения неопределенности
косвенных измерений, то есть путем переноса неопределенностей в значениях
параметров ![]() 1, s0 , η, ξ на неопределенность параметра жесткости.
1, s0 , η, ξ на неопределенность параметра жесткости.
Литература:
1. Вибрации в
технике. Защита от вибраций и ударов; Т.6: Справочник / Под ред. К.В. Фролова/.
М.: Машиностроение, 1981. - 456 с.
2. Закржевский М.В. Колебания
существенно-нелинейных систем.- Рига: Зинатне, 1980. - 190 с.
3.
Федотов, А.И. Теория измерений /А.И. Федотов, С.К. Лисин, Г.С. Морокина. –
СПб.: Изд-во Политех. ун-та, 2013. – 325 с.
4. Гурецкий В.В., Лисин С.К. Модели режимов и
устройства неразрушающего контроля твердости изделий. // Измерительная техника, 2006, №1.
5. Лисин С.К., Федотов А.И. Материалы 10-й
международной научно-практической конференции. Современные научные достижения.
Том 4, София, 2014, с. 38 – 44.
6.
Cyril M. Harris. Shock and Vibration Handbook. McGraw – Hill,
1996, 1000 p.
7.
Victor Wowk. Machinery Vibration: Measurement and Analysis. McGraw – Hill
Professional, 1991, 358 p.