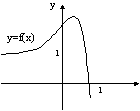
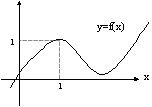
5. Ìàòåìàòè÷åñêîå ìîäåëèðîâàíèå
The possibility of using computer in learning the basics of mathematical
analysis in pedagogical high school
Omarova y.M
International Kazakh-Turkish University
H.A.Yasawi
Kazakhstan
Nowadays we look on volume of
computerization. Practically, there was no sphere, where wouldn’t use
computers: financial operations, engineering,
communications and printing, modeling
and construction of new objects
and more. It is difficult to imagine our life without these operating and multifunction tools. Therefore, it is
important to teach various computer skills at all levels of the education
system. Using micro-computer technology in education is a powerful new stimulus for the further development of teaching science. There is a need for research to find
new and effective techniques, methods of using computer technology that
enhance the ability of the educational
process. Pedagogical and methodological developments of recent years
demonstrate the full implementation of information and communication tools and
they have a priority for the further development of science. Today many leading
teachers increasingly refer to the use of these tools in modern educational
process: M.P Lapchik, V. A. Dalinger, K. A. Zuev, N.V. Sholokhov, P. I. Sovertkov, I.V. Robert, S.I.
Shapiro, B.S. Gershunsky and others. Most of them take the consideration of
various approaches to the use of computer technology as a learning tool.
The computer can act as a subject of study, as a
learning tool, as a tool for
scientific research. And it performs the following tasks: to perform
complex computing operations, analysis of the experimental results, the construction and
interpretation of mathematical models, and so on.
The use of computer in the learning activities are
mainly limited to its use as a "big calculator", "textbook
information" tool for controlling students' knowledge and less than as a
performer of other functions. However, this
reveals the advantages and opportunities for learning. When using the computer
students master the learning material at their own speed, and it refers to objective assessment of
their knowledge, carried out simultaneous feedback, they get a wide range of
information to be provided in various ways; teacher has an opportunity
to take into account the individuality of students, pay more attention to them,
get rid of routine work when searching for information, include various exercises, while spending a minimum
of time for creating tasks, and as a result, spend more time for improving his
intellectual level and professional skill. No doubt, such use
of computer solves many educational, psychological problems
during the learning. However, the possibilities of technical means
are much broader. In addition,
information technology not only has a
significant impact on the learning process, but
also on a development and education of
students. They stimulate and create motivation, provide the dynamism
of the learning process, stimulate learning
and cognitive activity. Information technology alone cannot always ensure
efficiency of learning, but they
can be a means of improving
the current educational process.
The primary role in their implementation
falls on the shoulders of school teachers, teachers of secondary and higher educational institutions. Consequently,
it is necessary to pay the attention to the preparation in pedagogical
high schools not only teachers of
computer skills, but also teachers of other disciplines (humanities and natural, mathematical cycles), the
basics of modeling with the use of the application software. Teachers
must be not only subject teachers,
but teachers who have got basics of didactics and
new technologies of education.
M.P.
Lapchik notes that computer science – it is not the content, it is the methodology, and that for this reason, all teachers - as a whole all the experts
must become teachers of computer skills,
and computer literacy of young people
must have formed in
a constant communication with the
computers in the classroom in all
subjects, and during the whole life of schooling. However, there
is a need for advanced
study of computer science as a
specialty. [6, p. 25].
Education in the
high school is getting particular importance due to the need to give future teachers suitable knowledge and methodological skills. Preparation of students of pedagogical
universities - future teachers
- should be organized in such a way that, having come to school, they
were able to work with students, using new approaches to learning.
In pedagogical high school on the
shoulders of the teachers have a responsibility not just for teaching
theoretical issues of specific course program, but they have to be specimen of
implementation of methodological, pedagogical and psychological theories in practice,
have to be the illustrative example, who teaches not only in words, but and applies
them in his lessons. Often, such cases can be observed: young teachers who have
studied five years of advanced pedagogical experience, they choose the way of
teaching, borrowed from their own teachers. Their selection is based on the
experience: they saw it and in this way they realized how to build their
organizational activities. Therefore, it is important not to promote future
teachers the use of computers in the classroom, but to apply and become a
real-life image of the implementation of this theory in the study of
educational material.
Such effective technical means, as the computer, may be used at all stages of study. Its use should not be limited to the laboratory studies; it may be lectures, practical lessons, tests, course and diploma projects.
Computer can simulate abstract objects, processes, phenomena;
process the information at extremely rapid rates in
perceiving the new academic content. Computer can make a demonstrational analysis
of the relationships, dependencies in the process of
understanding and generalization;
monitor an independent work, draw conclusions,
hypotheses and prognoses.
Computer serves as a generator of problem situations; manages independent work; analyzes the level of assimilation, when fixing the educational material.
Computer can serve as a simulator for the formation of skills and abilities; provide differentiated support and control for the learners. [8, p. 124-125].
In the learning process, turning on the computer should not be chaotic and aimless. Each study should be
well-considered, and involving information and communicative feature must be justified by the objectives, demands of the subject, time spending. The development of skills with the technical means necessary to carry out systematically throughout the course of study in high school.
The computer as a learning tool has another important advantage - its ability to represent various types of dependencies, numerical relations,
and so on, in a
visual form. During the lesson
happens the realization principles of clearness in a different level. The
particular interest presents modeling phenomena, which is not accessible to direct observation,
and also phenomena whose description has not developed a sufficient
mathematical tool and which can not be
demonstrated without the help of a computer within the classroom.
Visualization is not given due attention in the
traditional high school. It was found that 90% of information is about the surrounding reality, and person gets through the visual
analyzer, 9% - with the help of hearing, and 1% - with the help of touch. It confirms that the active use of the visual analyzer opens a new and great opportunity to improve the quality and effectiveness of education [8, p. 10]. This problem is also able to solve involved in the learning
process the
computer tools.
Here is given a statement: "Who
has not seen that out of 50 classmates at least 40 were disgusted and lost
heart because of abstract ideas, that are presented before they were becoming clear
in the examples taken from everyday practice" [3, p. 7]. The computer easily and naturally
enters into the world of mathematical abstraction at the expense of their
submission to the visual images, firmly imprinted in the minds of learners. Animation
allows you to recall material studied previously and is difficult, it activates
the formation of the cerebral cortex temporary bonds (associations). When students see as in the display
"come alive" mathematical formulations, their motivation increases,
grows interest to mathematics, expands their personal enrichment.
Fast computers open new opportunities in teaching (not only in pedagogical high
school) the foundations of mathematics. They help to disclose the possibility of mathematical methods better and train specialists, who
are able to use mathematical methods wider, fuller and faster. "The most important task of preparing for a mathematics teacher is to master
students and computer technologies - writes V. Dalinger - and the ability to apply them in the study and teaching disciplines of mathematical cycle "[4, p. 31].
Consider how you can use computer technology in relation to practical training
in mathematical analysis at the university.
Mathematical analysis in general takes
one of the leading places in the mathematical training of teachers. The ideas and methods of analysis
permeate the entire course of algebra 7-11 in a explicit and implicit form. The course of the mathematical
analysis in pedagogical high school is designed to equip students with
mathematical methods of judgment, raise their general level of mathematical
culture. It should be noted that
the general framework for the analysis causes students’ particular difficulties
in the perception of new concepts and, as a consequence of difficulties in
applying them to perform tasks. Considering
the high abstraction of educational material on mathematical analysis, it is
necessary increase the use of the visibility in its study, not only in learning
process of the theoretical materials, but also in the system of practice.
Let’s consider the main section of mathematical analysis - the theory of limits. Getting to know with it
begins in elementary
mathematics; where with the help of limiting process is determined the length of circumference
in a circle, volumes of solids of
revolution, the sum of infinitely decreasing geometric
progression, and so on. Operation of the limiting process is one of the basic operations of mathematical analysis.
The definition of
the limit of a sequence or function can be carried out by steps, with a clear
demonstration of these steps. It
is suitable to use the theory of stage
formation of mental actions (P.Y.Galperina – N.F Talyzina).
For the demonstration of the phenomena which process achieves its object
"Limit" situation,
let’s use the following in a dynamic
manner: swinging pendulum,
movement of the ball when you hit
it, the load suspended
on a spring in the damped oscillations.
A geometric sequence is represented on a number line as a series of points whose coordinates
are the corresponding elements of
post-sequence. For example, the sequence
is convergent, but the first is close to zero on only one side and the other from two sides.
Õ4 Õ3 Õ2 Õ1
![]() . .. . . . . . . õ
. .. . . . . . . õ
![]()
![]()
![]() 0 1 1 1 1
0 1 1 1 1
4 3 2
Õ1 Õ3 Õ5 Õ7 Õ6 Õ4 Õ2
![]() . . . . .. . . . . õ
. . . . .. . . . . õ
![]()
![]()
![]()
![]()
![]()
![]() -1 –
1 – 1 – 1
0 1 1 1
-1 –
1 – 1 – 1
0 1 1 1
3 5 7 6 4 2
Fig.1. the image on the number line sequences converging to zero.
For numerical sequence,
as well as for any function can be plotted. It is not
represented by a curve, and is made up of individual dots to the right of the y-axis. Also, these sequences may
be depicted in a coordinate plane
(Fig. 2).
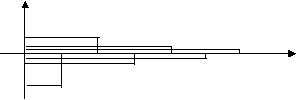
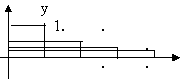 1.
1.
. .
0 1 2 3 4 õ 0 1 2 3 4 5
6 õ
à) -1 á)
Fig. 2. The image in the coordinate plane sequences converging to
zero.
We see that the point (members of the sequence) "gathering" around the point 0. The higher the number of points, the sequence will be closer to
0, though it never
reaches. Further useful
to give an example sequence with no chapel and
similarly present its geometric image. These sequences are set in the dynamics of the emergence of consistent points on the number line.
When writing the definition of limit of a sequence, you can use it as a geometric interpretation
of a, for any neighborhood where there is a number N such that all elements with numbers n> N are in this
neighborhood. The corresponding graphic
example is offered in the
following form.
Consistently held the line y = a, and
then, at a distance from it - parallel lines. And also consistently represent
the definition of a limit order. The number a is called the limit of the
sequence of AN, if for any positive integer there exists a number N = N (),
that for all n> N the inequality.
Thus, the number and the limit of the sequence (Fig. 3) provided on
the plane the points with coordinates (n; an). In accordance with the
definition, we chose a number arbitrarily, and all points are right of the line
x = N (), lie at a distance from and less than (lie in a strip)
Fig. 3. visual representation of the concept of "limit order"
An example of a numerical sequence,
which is equal to the limit and can serve as the
next task. Kg and a weight weighed on the
scale n times. At the first
weigh-in got a1
kg, the value of A1 is slightly different from the value of a.
Performing weighing two, we get the average value of the cargo - a2.
Next magnitude -
a3 kg - the average value of three consecutive readings on the scales, and so on. D. The resulting sequence
of the average values of cargo
weight limit is your true weight and,
although it is possible that none of
the value of AN is
not equal to a.
An example of a numerical sequence, which
is equal to the limit and can serve as the next task. Kg and a weight weighed
on the scale n times. At the first weigh-in got a1 kg, the value of A1 is
slightly different from the value of a. Performing weighing two, we get the
average value of the cargo - a2. Next magnitude - a3 kg - the average value of
three consecutive readings on the scales, and so on. D. The resulting sequence
of the average values of cargo weight limit is your true weight
and, although it is possible that none of the value of AN is not equal to a.
The generalization to arbitrary functions of the concept of limit of numerical
sequences (special form of functions) is the concept of limit of a function at
a point. The number A is the limit of the function f (x) as x tends to a, if
for any and¹ 0 such that for all x > d 0 there exists a number > enumber
, holdsd <satisfying condition⎟h - a⎟ [1, p.e <inequality⎮f (x) - A⎮ 124]. This definition of "Present" in the Microsoft PowerPoint
as a series of slides depicting phased introduction of the concept.
ó