Ст. гр. ФФ-21 Кучкин В. М.

К.е.н., доцент Иваницкая Е.В.

Национальный технический университет Украины "КПИ"

[Введите подзаголовок документа]

Конкуренция на рынке на основе модели поведения животных

Современная экономика – сложнейший организм, состоящий из разнообразия взаимодействующих структур и объединенных понятием «рынок». Ключевым понятием, выражающим основу рыночных отношений, является понятие конкуренции. В экономической теории конкуренцию можно рассматривать как степень состязательности на рынке.

Рынок совершенной конкуренции предполагает отсутствие власти производителя над рынком и установление цены через функцию спроса и предложения [1]. При этом характерно и наличие естественной борьбы «за выживание», стимулом же является стремление превзойти других.

В основе данного исследования конкурентного поведения на рынке лежит математическая модель конфликтного поведения животных, предложенная Зиманом в 1979 году [2]. Условно разделим производителей рынка на три типа: «ястреб», «голубь», «агрессивный трус». Все участники продают альтернативные товары. Чтобы получать преимущество в продажах, они могут либо рекламировать свой товар, либо уменьшать его цену. После выбора тактики, они узнают, что в данной ситуации сделали конкуренты. На основе полученной информации принимается решение о дальнейшем уровне цены.

Данную модель анализируем с точки зрения теории игр [3]. Производитель, применяющий стратегию i по отношению к противнику, применяющему стратегию j, получает «выигрыш» . В качестве выигрыша выступает чистый доход от продажи товара. Дополнительно считаем, что производители не могут менять свой тип. Полученная модель может описывать эволюцию трех типов производителей.

Тип производителя	Первоначальная тактика	Окончательная тактика
Ястреб	Уменьшение цен	Уменьшение цен
Голубь	Реклама товара	Фиксация цены
Агрессивный трус	Уменьшение цен	Фиксация цены

Пусть – доля производителей, применяющих i-ю стратегию. Считаем, что , тогда . Выигрыш производителей, применяющих i-ю стратегию против остальных участников рынка, составит ; где, А – платежная матрица, будет определена далее. Можно определить средний выигрыш определенного производителя в пределах своего типа . Следовательно, выгода от применения стратегии «і» равна:

В процессе торговли на рынке, определенный тип производителей может расширяться, как следствие оптимальности характерной для данного типа стратегией. Таким образом, скорость увеличения количества производителей применяющих i-ю стратегию выражается следующим образом:

Данное выражение фактически является системой дифференциальных уравнений описывающих рассматриваемые процессы на рынке.

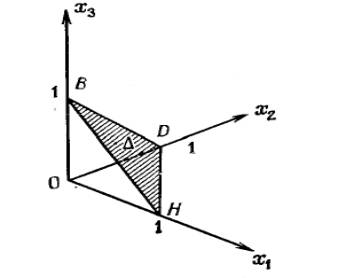
Динамике модели, описывающей данную конкуренцию на рынке характерно изменение только в области .

Если «ястреб» встречается с «голубем» или «агрессивным трусом», то он побеждает, так что . Если встречаются два «ястреба», то они сражаются до тех пор, пока один из них не получает травму. Оба «ястреба» выигрывают с равной вероятностью, и выигрыш равен . Если «голубь» встречает «ястреба» или «агрессивного труса», то он проигрывает, поэтому , но два «голубя» продолжают свои демонстрации друг перед другом, пока один из них не сдастся – . Наконец, «агрессивные трусы» проигрывают «ястребам» , выигрывают у «голубей» и имеют 50%-ный шанс выигрыша у себе подобных [2].

Полученная матрица А имеет вид:

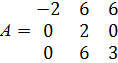
Данную систему проанализировано в рамках теории устойчивости [4] и получено устойчивые точки. Таковыми являются вершины треугольника , и точки , . Первые три точки иллюстрируют присутствие на рынке лишь одного типа производителей. Две последующие точки показывают, что на рынке будут сосуществовать либо «ястребы» и «агрессивные трусы», либо «ястребы» и «голуби». Причем появление третьего типа конкурентов на рынке приведет к исчезновению или «голубей», или «агрессивных трусов» [2].

Применение этой модели позволяет выделить наиболее конкурентоспособных производителей, ими являются те, кто относится к типу «ястреб». То есть те, кто продают товары по минимально возможным ценам. Это выгодно для потребителей. Очевидно, что два других типа производителей остаются в проигрыше, так как отказываются понижать цену дальше. Также вероятно существование на рынке одновременно типа «ястреб» и любого другого типа. В основном это происходит за счет рекламы («голуби») и первоначального понижения цен («агрессивный трус»), что помогает существовать соответствующим типам, а «ястреб» выживает за счет окончательного уменьшения цены товара. Теория нелинейного анализа подчеркивает асимптотическую устойчивость последних двух случаев, то есть в процессе развития рынка такое соотношение типов будет наиболее оптимальным для производителей [4].

Таким образом, природа и характер конкурентного состязания на рынке аналогичны поведению соперников в живой природе, и способствуют прогрессу и поступательному движению цивилизации в целом. Результатом конкурентной борьбы есть «выживание», которое возможно только при учете интересов потребителей, т.е. общества в целом. В ходе конкуренции, рынок из многообразия товаров отбирает только нужные потребителям, определяя тем самым доминант производителя. Прочие производители остаются менее востребованными, и их «популяция» сокращается.

Литература

1. Портер М. Конкуренция / Майкл Портер; пер. с англ. — С.Пб.: Вильямс, 2002. — 495 с.

2. Zeeman E. C. Population Dynamics from Game Theory, Int. Conf. (1979) Global Theory of Dynamical Systems, Northwestern-University, Evanston, IL.

3. Мак-Кинси Дж. Введение в теорию игр / Дж. Мак-Кинси — М.: Гос. изд-во физ-мат литературы, 1960. — 420 с.

4. Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями / Д. Эрроусмит , К. Плейс — М.: Мир, 1986. — 243 с.