ДЕФОРМАЦИЯ
ДОМЕННОЙ СТЕНКИ ПРИ НАЛИЧИИ АССИММЕТРИЧНО РАСПОЛОЖЕННОЙ МАГНИТНОЙ
НЕОДНОРОДНОСТИ
Акимов
М.Л., Поляков П.А., Усманов Н.Н.
МГУ
им. М. В. Ломоносова, физический факультет
Известно, что в ферромагнитных пленочных материалах энергетически выгодно возникновение магнитного доменного упорядочения [1]. В работах [2-4] были получены смешанные доменные структуры, состоящие из полосовой доменной структуры и магнитной неоднородности в форме цилиндра и эллипса.
Рассмотрим
единичный изолированный полосовой домен при наличии внутри него цилиндрической
магнитной неоднородности радиуса R. Изолированный
полосовой домен ширины w=2a,
расположенный вдоль координатной оси x в бесконечной пленке
толщины h, с – параметр несимметричности. Координатная ось z направлена перпендикулярно
плоскости пленки, а ось y – перпендикулярно
доменной стенке. Начало системы координат помещено в центр ЦМД.
Магнитостатическое поле рассеяния данной цилиндрической магнитной
неоднородности исказит форму полосового домена и приведет к зависимости его
ширины от координаты x.
Пусть функции ![]() и
и ![]() определяют изгибы доменных стенок.
Вычисляя вариационные производные функционала изменения магнитостатической
энергии
определяют изгибы доменных стенок.
Вычисляя вариационные производные функционала изменения магнитостатической
энергии ![]() ,
, ![]() , получаем систему нелинейных функциональных интегральных уравнений для
функций
, получаем систему нелинейных функциональных интегральных уравнений для
функций ![]() и
и ![]() , которые при относительно малых искривлениях доменных границ можно
линеаризовать. Раскладывая функции
, которые при относительно малых искривлениях доменных границ можно
линеаризовать. Раскладывая функции ![]() и
и ![]() в пределах интегрирования в ряд,
имеем систему уравнений. Уравнения системы являются
линейными интегральными уравнениями типа свертки и могут быть решены методом
преобразования Фурье. Проводя преобразование Фурье, получим следующие
выражения для форм искажения доменных границ полосового домена:
в пределах интегрирования в ряд,
имеем систему уравнений. Уравнения системы являются
линейными интегральными уравнениями типа свертки и могут быть решены методом
преобразования Фурье. Проводя преобразование Фурье, получим следующие
выражения для форм искажения доменных границ полосового домена:
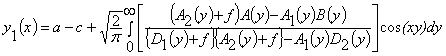 ,
,
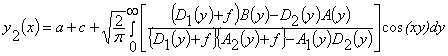 , (1)
, (1)
где
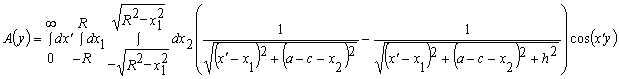
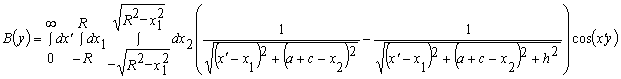
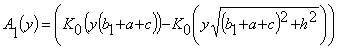 ,
,
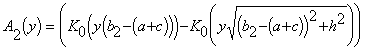 ,
,
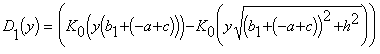 ,
,
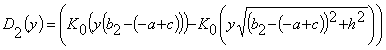 ,
,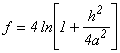 ,
,
![]() и
и ![]() - максимальные
значения функций
- максимальные
значения функций ![]() и
и ![]() , описывающих формы искажений доменных границ
полосового домена вследствие магнитостатического поля рассеяния несимметричного
цилиндрического домена.
, описывающих формы искажений доменных границ
полосового домена вследствие магнитостатического поля рассеяния несимметричного
цилиндрического домена.
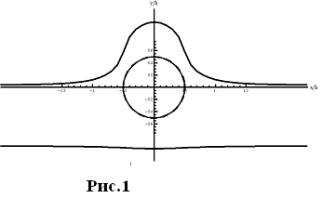
Форма полосовой
доменной структуры при наличии несимметрично расположенного
цилиндрического магнитного домена в магнитной пленке показана на рис. 1(на
графике по осям x
и y
отложены безразмерные величины x/h и y/h).
 Целью
проведенного эксперимента было получение смешанной доменной структуры,
состоящей из полосового домена и локализованного внутри него
цилиндрического магнитного домена ЦМД, смещенного относительно центральной оси
полосового домена. Для экспериментальной
реализации заданной конфигурации
магнитных структур использовалась монокристаллическая пленка феррит-граната состава
Целью
проведенного эксперимента было получение смешанной доменной структуры,
состоящей из полосового домена и локализованного внутри него
цилиндрического магнитного домена ЦМД, смещенного относительно центральной оси
полосового домена. Для экспериментальной
реализации заданной конфигурации
магнитных структур использовалась монокристаллическая пленка феррит-граната состава ![]() с ориентацией
(210). Выбранный образец характеризовался следующими параметрами:
толщина пленки h@13
с ориентацией
(210). Выбранный образец характеризовался следующими параметрами:
толщина пленки h@13![]() m,
угол наклона оси легкого намагничивания
m,
угол наклона оси легкого намагничивания ![]() @300,
намагниченность насыщения 4pMs@60 Gs.
@300,
намагниченность насыщения 4pMs@60 Gs.
 Для создания заданного
магнитного состояния применялся метод описанный в работе [2]. После трансформации
ЦМД в полосовые домены в нашем эксперименте также оставался один единственный
ЦМД. Однако из-за влияния дефекта этот ЦМД был
локализован не на центральной оси полосового домена. Ширина
полосового магнитного домена, внутри которого существовал ЦМД, составляла 13 мкм.
Наличие ЦМД внутри полосового
домена влияет на форму доменных стенок полосового домена. Ассиметричное
положение ЦМД приводит к существенному различию искривлений обеих границ (Рис.2). Как видно из рисунка доменная стенка, ближе
к которой ЦМД локализован, имеет большие искажения. Максимальное значение
величины изгиба доменной границы полосового домена полученное в эксперименте составило 15,5 μm. Теоретический расчет величины максимального
изгиба доменной границы полосового домена по формуле (1) при параметрах, соответствующих экспериментальным
данным R = 6,5 μm
— средний радиус цилиндрического магнитного домена, с = 6 μm
— параметр несимметричности, дает значение 13,9 μm.
Для создания заданного
магнитного состояния применялся метод описанный в работе [2]. После трансформации
ЦМД в полосовые домены в нашем эксперименте также оставался один единственный
ЦМД. Однако из-за влияния дефекта этот ЦМД был
локализован не на центральной оси полосового домена. Ширина
полосового магнитного домена, внутри которого существовал ЦМД, составляла 13 мкм.
Наличие ЦМД внутри полосового
домена влияет на форму доменных стенок полосового домена. Ассиметричное
положение ЦМД приводит к существенному различию искривлений обеих границ (Рис.2). Как видно из рисунка доменная стенка, ближе
к которой ЦМД локализован, имеет большие искажения. Максимальное значение
величины изгиба доменной границы полосового домена полученное в эксперименте составило 15,5 μm. Теоретический расчет величины максимального
изгиба доменной границы полосового домена по формуле (1) при параметрах, соответствующих экспериментальным
данным R = 6,5 μm
— средний радиус цилиндрического магнитного домена, с = 6 μm
— параметр несимметричности, дает значение 13,9 μm.
Проведенные эксперименты показывают, что рассмотренная теоретическая модель пригодна для описания изменения формы доменной стенки для доменной структуры с ассимметричной локализацией ЦМД.
Литература
1.
Ландау Л. Д.,
Лифшиц Е. М. Электродинамика сплошных сред. М.: Наука. 1992, 664 с.
2.
М. Л. Акимов,
П. А. Поляков, Н. Н. Усманов. ЖЭТФ, 121 (2002) с. 347-353.
3. M. L.
Akimov, P. A. Polyakov, Y. V. Starokurov, N. N. Usmanov,
Y. N. Fedyunin. Physica B 405 (2010) 2376–2379.
4.
М. Л. Акимов,
П. А. Поляков. Вест. Моск. ун-та, сер. 3, физ. астр., 2004, № 2,
с.47-50.