УДК: 67.02

Овчинников В.А.1, Ахметшин Р. Г.2, Разин А.В3., Порохов Е.С.4, Яковлев А.Н.5

1 - инженер, ассистент кафедры ЛИСТ НИ Томский Политехнический университет;

2 - инженер проектировщик НИ Томский Политехнический университет;

            3 - инженер, ассистент кафедры ЛИСТ НИ Томский Политехнический университет;

     4 – аспирант НИ Томский Политехнический университет;

5 - к.ф.-м.н., доцент, заведующий кафедрой ЛИСТ НИ Томский Политехнический университет.

Математическое моделирование взаимодействия лазерного излучения с веществом при селективном лазерном спекании

1.    Введение

Селективное лазерное спекание (СЛС) относится к аддитивным технологиям, имеет широкую область применения в различных отраслях промышленности. Данная технология может быть применена, как для упрочнения поверхности, так и для послойного выращивания деталей. Последнее имеет огромное значение, при прототипировании деталей, когда оригинальные литьевые металлические детали заменяются образцами, выполненными при помощи СЛС синтеза. Использование СЛС не требует подстройки производственного процесса для новых деталей, и позволяют изготавливать совершенно новые изделия. Современные установки СЛС позволяют послойно выращивать детали, по своим характеристикам приближающиеся к литым. Благодаря этому СЛС постепенно расширяет круг своих приложений [1-3].

Аддитивная технология СЛС — это процесс, при котором, согласно технологической карте, выполняется лазерная наплавка для формирования детали, путем повторения различных технологических операций: прогрева подложки, нанесения тонкого слоя порошка и сплавления по текущему сечению детали при помощи сканирующей лазерной системы. Это позволяет получать детали любой формы. Оставшийся после технологической обработки несплавившийся порошок удаляется с поверхности детали путем пескоструйной обработки [4].

В работе [5] показано, что характеристики лазерного луча и параметры лазерного импульса оказывают определяющее воздействие на качество готового изделия, его плотность, пористость и функциональные характеристики. Оптические свойства среды и лазерного пучка в совокупности при лазерном сплавлении определяют эффективный коэффициент энерговклада. Коэффициент энерговклада — это основной технологический параметр теплового воздействия лазерного излучения, характеризующий процесс плавления порошкообразного слоя в адиабатических условиях. Кроме того, на качество наплавляемого слоя влияют особенности распространения лазерного излучения в порошкообразной среде с эффектами многократного рассеяния. Оценка влияния эффектов многократного оптического рассеяния при взаимодействии лазерного излучения с порошкообразным слоем наплавляемого вещества имеет огромный практический интерес, позволяет лучше прогнозировать пористость, прочность и другие механические характеристики изделий, производимых при помощи технологии СЛС.

Данное исследование посвящено оценке влияния распределения освещенности в перетяжке лазерного луча, частоты следования импульсов и скорости движения луча, формируемого сканаторной системой на эффективный коэффициент энерговклада и характерную глубину проплавления порошкового слоя.

При выполнении СЛС композитной смеси порошков над подложкой требуются оптимальные характеристики лазерного луча, которые необходимо получить имитационным моделированием явлений многократного рассеяния фотонов в порошкообразной среде при воздействии лазерного излучения. Для этой цели использовался метод Монте-Карло и теория рассеяния Ми. Последняя была использована для определения оптических характеристик среды.

2.    Экспериментальный стенд

Исходными параметрами и граничными условиями для моделирования процесса СЛС были технические характеристики установки «Квант» для 3D печати методом СЛС разрабатываемой в НОЦ «Современные производственные технологии» НИ ТПУ [6]. Ниже на рисунке 1 приведена блок схема установки.

 

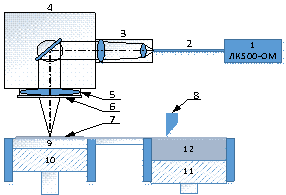
Рисунок 1. Блок схема установки «Квант» для 3D печати методом СЛС. 1 — волоконный лазер ЛК500-ОМ, 2 — оптическое волокно, 3 — коллиматор, 4 — сканаторная головка Lscan, 5 — объектив сканаторной головки, 6 — защитное стекло, 7 — слой порошка, 8 — устройство для нанесения тонкого слоя порошка 100 мкм (ракель), 9 — подложка, 10 — подъемная платформа для формирующейся детали, 11 — подъемная платформа с резервуаром для порошка 12.

 

Для генерации лазерного излучения в установке применен мощный волоконный лазер ЛК-500-ОМ с непрерывным одномодовым излучением, которое возникает в оптоволоконном активном элементе 2 и направляется в коллиматор 3. Сканаторная головка 4 обеспечивает сканирование лазерным лучом по сечению изделия при помощи управления поворотными зеркалами. Излучение в сканаторной головке направляется в объектив 5, проходя через защитное зеркало 6, фокусируется на поверхности тонкого слоя порошка 7. Устройство нанесения тонких слоев 8 забирает порошок из резервуара 12 с подъемной платформы 11 и наносит его на подложку 9. Подъемно-опускающаяся платформа 10, на которой формируется изделие, выводит перетяжку лазерного луча на поверхность порошка.

Установка «Квант» позволяет проводить гибкую настройку в широком диапазоне параметров лазерного луча и параметров развертки сканаторной системы. Параметры установки «Квант» приведены в таблице 1.

 

Таблица 1. Параметры лазерной системы

Тип лазера

Иттербиевый оптоволоконный

Длина волны, λ

1,07 мкм

Мощность излучения, P

150 – 400 Вт

Диапазон скоростей движения луча оптической сканаторной головки, v

0-1200 мм/с

Режим развертки

Зигзагообразная, с гашением излучения при возврате луча

Диаметр зоны воздействия, d

100 мкм

Рабочая область

10x10 см2

3.    Численные расчеты

Объектом исследования в работе являлась смесь ультрадисперсных порошков титана и ниобия. Ультрадисперсный порошок титана является сильно поглощающей средой для длины волны 1,07 мкм [7], также, как и ниобий. Поскольку как уже было оговорено выше оптические параметры порошка значительно влияют на световой режим, требуется подробное исследование рассеивающих свойств смеси.

Для получения основных оптических параметров вещества: коэффициент поглощения (μ) и показатель рассеяния (β), воспользуемся теорией рассеяния Ми [8] на сферических частицах. При помощи программного пакета MiePlot [9] рассчитанны относительные коэффициенты рассеяния и поглощения на сферических частицах различного диаметра. Исходными параметрами являются: показатель преломления n, равный 3,5 для титана [7] и 2,48 для ниобия [10]; диаметр частиц 0,01 – 100 мкм. Расчет производится для длины волны излучения λ = 1,07 мкм. На рисунке 2 показаны результаты расчета относительных сечений поглощения и рассеяния для разных диаметров частиц.

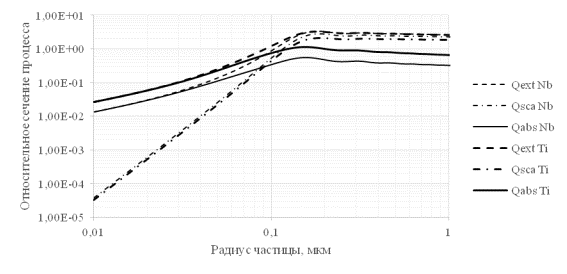
Рисунок 2. Значения относительных коэффициентов поглощения Qabs и рассеяния Qscat на сферической частице, рассчитанных в зависимости от радиуса частиц для Ti и Nb. Qabs — относительное сечение поглощения, Qsca — относительное сечение рассеяния, Qext — относительное сечение ослабления

 

Средний диаметр частиц исследуемого порошка Ti составляет d = 20 мкм, а Nb 1 мкм. Соответственно рассчитанные коэффициенты имеют значения: Qscat = 1,689, Qabs = 0,479 для Ti и Qscat = 2,245, Qabs = 0,318 для Nb. Для определения показателя поглощения и коэффициента рассеяния воспользуемся формулами полученным на основании закона Бэра [11]:

                                                                                          (1)

                                                                                         (2)

где r – радиус одной частицы, nc – концентрация частиц в объеме порошка, Qscat – относительное сечение рассения, Qabs – относительное сечение поглощения, μ – показатль поглощения среды, β – показатель рассения.

В результате расчета и суммирования показателей для компонентов смеси Ti и Nb получаем для порошковой среды: μ = 288,6 см-1, β = 835,5 см-1. Однако, значения Qscat и Qabs при больших концентрациях частиц сильно зависят от nC и формулы (1, 2) справедливы только с учетом многократного рассеяния.

Метод Монте-Карло позволяет получить точное численное решение уравнений переноса излучения [12] если известны оптические характеристики элементарного объема рассеивающей среды. Используя имитационное моделирование методом Монте-Карло по алгоритму, опубликованному в труде [13], можно прогнозировать результаты взаимодействия лазерного излучения с веществом, зная оптические характеристики этой среды, а также, определить эффективную глубину проникновения лазерного излучения zef. Поскольку в расчетах для нахождения светового режима в объеме рассеивающей среды не учитываются нелинейные процессы при взаимодействии лазерного излучения с веществом решено было использовать величину характеризующую значение светового потока, приходящееся на толщину элементарного слоя рассеивающей среды, по отношению к падающему на поверхность световому потоку, через элементарную площадку на поверхности вещества:

                                                                          (3)

здесь  — световой поток через элементарный слой вещества на глубине z,  — освещенность элементарной площадки на поверхности образца в радиальной системе координат ,  — элементарная площадка на поверхности образца,  — толщина элементарного слоя.

Численным методом Монте-Карло было получено распределение относительной поглощаемой лазерной мощности A(z) по глубине взаимодействующего с лазерным излучение порошкообразного слоя (см. рисунок 2). Для расчета был использован программный пакет MCML [14].

 

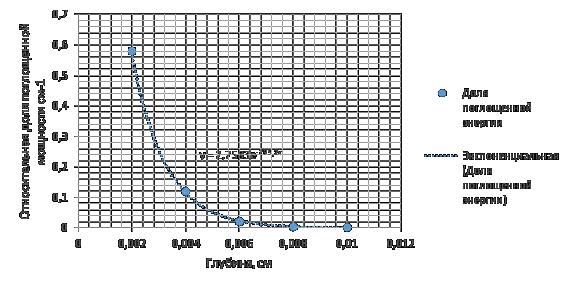
Рисунок 3. Доля поглощенной энергии в зависимости от глубины воздействия

 

Согласно рисунку 3 распределение поглощаемой лазерной мощности по глубине рассеивающей среды соответствует экспоненциальному закону, что укладывается в рамки теории однократного рассеяния. Также экспоненциальное распределение поглощаемой энергии согласуется с законом Бугера-Ламберта-Бэра. Однако эффективный показатель ослабления для полученного распределения значительно меньше показателя ослабления, который дает теория однократного рассеяния и закон Бугера. Таким образом, эффекты многократного рассеяния увеличивают характерную глубину проникновения излучения.

Для того, чтобы определить, какую энергию необходимо затратить, чтобы расплавить весь слой вещества по всему сечению перетяжки луча диаметром в 100 мкм, необходимо рассчитать эффективную глубину проникновения лазерного излучения.

Для нахождения эффективной глубины проникновения лазерного излучения zef воспользуемся формулой, полученной из закона Бугера [11]:

                                        .

Отсюда для zef получаем

                                       ,                                             (4)

где A1 – коэффициент поглощения на глубине z1, A0 – коэффициент поглощения на глубине z0.

Произведя расчет по формуле (4) на основании данных по распределению поглощаемой мощности излучения приведенных на рисунке 3, получаем: zef = 33 мкм.

Зная параметры поглощенного веществом потока лазерного излучения, а также теплофизические константы материала, можно оценить температуру нагрева вещества, а также количество энергии, необходимой для расплава всего порошкового слоя. Для определения энергии нагрева, и расплава слоя вещества необходимо определить объем V зоны проникновения лазерного излучения и прогретого слоя. Используя характерную величину пробега теплоты , легко получить оценку для прогреваемого объема вещества под воздействием лазерного излучения [1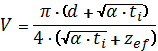5]:

                                      ,                                            (5)

где α – температуропроводность, ti – характерное время воздействия импульса лазерного излучения.

Из формулы (5) видно, что объем зоны прогрева зависит, прежде всего, от характерного времени воздействия лазерного излучения, которое тем меньше, чем выше скорость движения луча по поверхности образца. Так как, система позволяет гибко регулировать скорость движения сканаторной системы, есть возможность регулировать характерное время воздействия, которое будет определяться отношением скорости движения лазерного луча к диаметру зоны воздействия (). Для того, чтобы определить, какую энергию необходимо затратить для нагрева и расплава вещества, воспользуемся традиционным уравнением [16]:

                                                                                                                  (6)

где λ – удельная теплота плавления, ρ – плотность порошка, C – удельная теплоемкость. На основании формул (5, 6) и теплофизических параметров элементов смеси, можно найти параметры лазерного излучения для плавления слоя толщиной 100 мкм. В результате численного исследования для полного проплавления был определен режим со скоростью движения лазерного луча по поверхности порошка 0,07 м/с и мощностью лазерного излучения 25 Вт. Доля поглощенной энергии лазерного излучения в этом режиме составляла 75% от падающего потока. Количество энергии, затрачиваемой на прогрев и расплав слоя вещества, при этом режиме воздействия составляет 0,027 Дж, а глубина воздействия, согласно расчету в программном пакете MCML и постобработки данных, составляет 98,3 мкм. Видно, что при оптимизированных режимах СЛС будет иметь место проплавление порошкового слоя композиции титана с ниобием.

Работа выполнена при финансовой поддержке Российского научного фонда, грант 15-19-90/91. Авторы признательны Шаркееву Ю. П. за плодотворное обсуждение результатов работы.

4.    Заключение

Выполнено моделирование процесса СЛС с использование лазерного луча непрерывного действия, обеспечивающего проплавление порошковой композиции титана и ниобия толщиной до 100 мкм. Определяющими параметрами энерговклада лазерного луча являются скорость перемещения луча по поверхности порошковой композиции и мощность лазерного излучения, а также рассеивающие свойства частиц Nb и Ti. Обнаружено, что световой режим в объеме порошковой смеси Nb и Ti характеризуется экспоненциальной зависимостью ослабления излучения с глубиной, однако, эффективный показатель ослабления данного режима значительно превышает показатель ослабления, полученный по формуле Бугера-Ламберта-Бэра. В результате многократного рассеяния эффективные сечения рассеяния и поглощения также значительно превышают данные на основе теории Ми. Таким образом, в порошковой среде Nb и Ti формируется сложный световой режим в условиях многократного рассеяния света, в котором с одной стороны возникают большие потери излучения за счет диффузного отражения от поверхности порошковой смеси, а с другой стороны — за счет условий многократного рассеяния света увеличивается эффективная глубина проникновения излучения.

СПИСОК ЛИТЕРАТУРЫ

1.        Сапрыкин А. А., Дудихин Д. В., Бабакова Е. В. Перспективы создания изделий методом селективного лазерного спекания // Актуальные проблемы современного машиностроения. – 2014. – С.14-16.

2.        Григорьев С. Н., Грибков А. А. Оптимизация точности элементов дозирующей системы // Техника и технология. – 2006. – № 5. – С.73-79.

3.        Назаров А. П. Особенности конструкции машин для селективного лазерного спекания // Вестник МГТУ «Станки». – 2013. – № 1 (24), – С.76-79.

4.        Tilghman B. Cutting and engraving stone, metal, glass, &c. No. 108, 408. Patented Oct. 18, 1870.

5.        Харанжевский Е. В. Ипатов А. Г., Николаева И. С. Влияние параметров обработки на плотность покрытий из твердого сплава, полученного короткоимпульсным селективным лазерным спеканием // Вестник Удмуртского университета. – 2014. – № 1 – С. 51-56.

6.        Современные производственные технологии ТПУ // URL: spt.tpu.ru

7.        Johnson P. and Christy R. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd, Phys. Rev. B 9, 5056-5070 (1974)

8.        Mie, Gustav. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen / Mie, Gustav. // Annalen der Physik – 330 (3) –pp. 377-445.

9.        Philip Laven. Simulation of Rainbows, Coronas, and Glories by use of Mie Theory / Philip Laven // Applied Optics. – 2003. – Volume 42. – Issue 3, –
pp. 436-444

10.    D. L. Windt et al. Optical constants for thin films of Ti, Zr, Nb, Mo, Ru, Rh, Pd, Ag, Hf, Ta, W, Re, Ir, Os, Pt, and Au from 24 Å to 1216 Å, Appl. Opt. 27, 246-278 (1988)

11.    Бугер, Пьер. Оптический трактат о градации света / Пьер Бугер; пер. Н. А. Толстой, П. П. Феофилов; ред. и коммент. А. А. Гершун.– Ленинград : Изд-во АН СССР, 1950.– 479 с. : рис.– (Классики науки).

12.    Иванов А. П. Оптика рассеивающих сред. — Мн.: Наука и техника, 1969. — 592 с.

13.    S. A. Prahl, M. Keijzer, S. L. Jacques, A. J. Welch; A Monte Carlo Model of Light Propagation in Tissue; SPIE Institute Series, vol. 5, pp. 102 – 111 (1989).

14.    Wang, L-H, S.L. Jacques, L-Q Zheng: MCML - Monte Carlo modeling of photon transport in multi-layered tissues // Computer Methods and Programs in Biomedicine 47:131-146, 1995.

15.    Лосев В.Ф., Морозова Е. Ю., Ципилев В. П.  Физические основы лазерной обработки материалов // Издательство Томский политехнический университет. – 2011. – C.10-12.

16.    Фриш С.Э., Тиморева А.В. Курс общей физики. Том 1. Физические основы механики, молекулярная физика, колебания и волны / 11-е издание. М.: ФИЗМАТГИЗ, 1962. - 467 стр.