Строительство и архитектура /3. Cовременные технологии строительства, реконструкции и реставрации.

К.т.н. Бубнович Э.В., магистрант Бондаренко Д.М.

Казахстан, г. Алматы, КазНИТУ им. К.И. Сатпаева

Вынужденные колебания радиальных вантовых систем

Система обыкновенных дифференциальных уравнений в матричном виде:

(1)

Здесь представляют собой симметричные матрицы масс, демпфирования и жесткости; =col() и col() – векторы обобщенных координат и интенсивности динамической нагрузки; - вектор нелинейного влияния, равный

) =

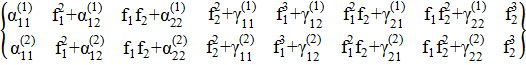
– динамическая нагрузка.

1.Полагая в формуле (1)

где – частота внешнего воздействия, получим дифференциальное уравнение вынужденных колебаний радиальной вантовой системы:

(2)

Для исследования поставленной задачи применим метод гармонической линеаризации. Рассматривая этот метод применительно к системе (2), обобщим его для систем со многими степенями свободы.

Как и во всех приближенных методах, здесь заранее предопределяется форма искомого решения, которая берется в виде

(3)

Линеаризуя (2), получим

(4)

Где матрица , а также вектора имеют тот же смысл, что в формулах.

С другой стороны, нелинейную функцию многих переменных можно разложить в многомерный ряд Фурье. В случае функции двух переменных, отбрасывая высшие гармоники, будем иметь

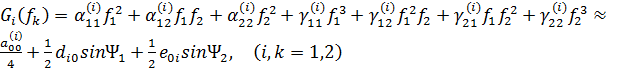(5)

Здесь коэффициенты гармонической линеаризации , определяют по формулам

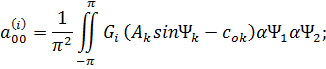
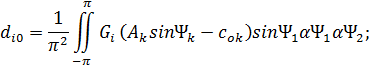
(6)

Для того, чтобы при отыскании функции гармонического вида можно было нелинейные функции заменить линейными, типа

необходимо и достаточно, чтобы коэффициенты матрицы были выбраны следующим образом:

(7)

Для определения постоянных имеем систему двух алгебраических уравнений.

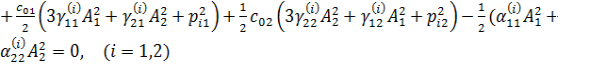(8)

Таким образом, исследование системы (2.32) сведено к исследованию линейной системы

(9)

2. Для простоты анализа сначала предположим, что вектор внешнего воздействия принят в форме Тогда выражения для комплексных амплитуд колебаний будут иметь вид

(10)

где

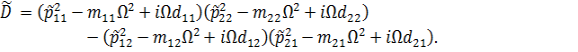
Формулы (10) представляют амплитудно-частотные зависимости вынужденных колебаний радиальной вантовой системы.

Пусть значение так, что им можно пренебречь. В этом случае:

(11)

где

(12)

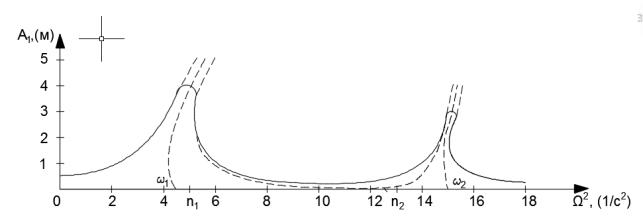
Рис.1. Амплитудно-частотная характеристика колебаний радиальной вантовой системы.

Амплитудно-частотная зависимость , представлена на рис.1, на котором пунктиром отмечены амплитуды колебаний в той же системе без демпфирования. Из графика видно, что при частоте возмущающей силы, равной второй парциальной частоте системы, т.е. при амплитуда колебаний , при отсутствии затухания, становится равной нулю.

3. Рассмотрим случай, когда вектор обобщенных сил равен . Перепишем уравнение (9) в форме

(13)

Где ; ,

(i,j =1,2)

Частное решение этой системы, соответствующее установившимся колебаниям, будем искать в виде

(14)

Подставляя это решение в систему (13) и производя некоторые преобразования получим

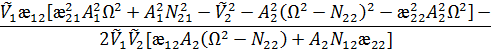
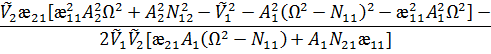
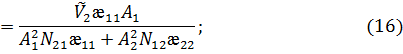
(17)

Выражения (15) ÷ (17) выведены при условии, что и один из элементов мвтрицы не равен нулю.

На основании последних соотношений можно построить амплитудно- и фазово-частотные зависимости.

Литература:

1. Бубнович Э.В., Бондаренко Д.М., К вопросу об уравнениях колебаний радиальных вантовых систем. Сборник Наука и Техника, Пше́мысль, 2014. 80-84 стр.

2. Новодворский В.Э. Обобщение теорем строительной механики. Вестник инженеров и техников. 1931, №8.

3. Пановко Я.Г. Введение в теорию механических колебаний. М.: Наука, 1971.

4. Ивович В.А. Динамический расчет висячих конструкций. М.: Стройиздат, 1975.