УДК 681.5.015

 

Д.т.н., проф. Рутковский А.Л., к.т.н. Ковалева М.А., Тедеева Н. В.

ВГБОУ ВПО «Северо-кавказский горно-металлургический институт (государственный технологический университет)»,Россия, г. Владикавказ.

 

ПОСТРОЕНИЕ СИСЕМЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ СЛОЖНЫМ ТЕХНОЛОГИЧЕСКИМ КОМПЛЕКСОМ

 

Аннотация: Целью настоящей работы является развитие математических методов и постановка задач оптимального управления множеством взаимосвязанных траекторий – технологиями непрерывных технологических процессов и создание численных методов их решения.

Ключевые слова: автоматизированные системы; математические методы; множество взаимосвязанных траекторий; оптимальное управление; финитное управление.

 

SISTEM IS CREATION OF OPTIMAL CONTROL OF THE DIFFICULT TECHNOLOGICAL COMPLEX

 

Abstract: The aim of this work is the development of mathematical methods and formulation of optimal control of a plurality of interconnected paths - technology of continuous technological processes and creation of numerical methods for solving them .

Keywords: automated systems; mathematical methods; a plurality of interconnected paths; optimal control; finite control .

 

При разработке автоматизированной системы оптимального управления группой аппаратов, в которых протекают сложные технологические процессы, возникает задача оптимального управления отдельным аппаратом с закрепленными концами и заданном времени протекания [1]. Следует отметить, что технологические процессы цветной металлургии описываются сложными нелинейными обыкновенными дифференциальными уравнениями или в частных производных. В первом приближении будем рассматривать класс металлургических процессов, описываемых нелинейными обыкновенными дифференциальными уравнениями типа

,                                                                                         (1)

где х — n-мерный вектор состояния; u — n-мерный вектор управления, F — n-мерная вектор-функция, отражающая основные физико-механические особенности технологического процесса. Задачу оптимального управления сформулируем следующим образом.

Необходимо найти такое допустимое управление u Є U, которое переводит систему (1) из некоторого начального состояния х0 в заданное конечное состояние за заданное время Т, минимизируя при этом некоторый критерий оптимальности I, который в общем виде можно записать как [1]

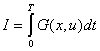                                                                                      (2)

Хорошо известно, что при решении такой задачи оптимального управления при использовании вариационных условий возникает необходимость решения соответствующей краевой пограничной задачи. Аппарат теории моментов же дает эффективные точные и приближенные методы вычислений оптимальных управлений, при этом решаются и краевые задачи [2].

Поставленную задачу оптимизации можно отнести к классу финитных задач управления, поскольку управления и без всякой потери общности можно считать равным нулю вне заданного конечного интервала времени [0, T], для решения которой можно использовать мощный аналитический аппарат теории целых функций экспоненциального типа и теорию интерполяции Лагранжа.

Однако этот математический аппарат применим лишь к решению задач финитного управления системами, которые описываются линейными соотношениями: дискретными линейными уравнениями, обыкновенными дифференциальными уравнениями и т.д.

Поэтому непосредственно использовать метод решения задач финитного управления, предложенный А. Г. Бутковским [2], нельзя.

Рассмотрим эту задачу несколько под другим углом зрения [3]. Пусть существует некоторая траектория g(t), удовлетворяющая условиям поставленной задачи, но не являющаяся оптимальной. Разобьем эту траекторию g(t), 0 ≤ t≤ T нa n отрезков, длительность существования которых равна Т/п = Т0. Разложим уравнение (1) в ряд Тейлора в окрестности некоторой точки g(iT0), принадлежащей допустимой траектории g(t),0 ≤ t ≤ T, и ограничимся первыми двумя членами, т.е.

 ,        (3)

Тогда линеаризованное уравнение движения системы (1) примет вид:

                                                                                           (4)

где Аi — матрица размера (п×п), элементами которой являются первые производные вектор-функции F(x, u) по координатам вектора состояния х в точках х (iT0) и u(iТ0); Вi — матрицa размера (nХn). элементами которой являются первые производные вектор-функции F (x, u) по координатам вектора управления u в точках х (i Т0) и u(i Т0);

Здесь ,  – вариации координат вектора x и вектора управления u.

Теперь можно сформулировать задачу финитного управления для системы (4) на отрезке (i T0, (i+1) T0) необходимо найти такое управление u, которое переводит систему (4) из некоторого начального состояния х (i T0) в точку x ((i+1) Т0) за время Т0.

Так как в дальнейшем необходимо использовать теорему Винера-Пэли, которая формулируется для функций, определенных на симметричном относительно начала координат отрезке, будем рассматривать систему (4) и функцию u(t) на отрезке (-τ, τ), а не (iT0,(i+l)Т0), положив τ=Т/2 и произведя сдвиг области определения функций на n вперед. Как известно, для преобразованных по Фурье функций это соответствует умножению их на величину .

Будем считать, что U(t) — финитная функция, определенная на отрезке [-τ, τ] и, по крайней мере, интегрируемая с квадратом, т. е. . Очевидно, что координаты вектора y(t) также будут интегрируемы с квадратом на отрезке [-τ, τ].

Начальное условие для системы (4) запишем в виде

у(-τ) = x((i + 1) Т0 - х (iТ0)) = У0.                                                    (5)

Тогда конечное условие при t=i будет иметь вид:

y(+τ) = 0.                                                                                        (6)

Таким образом, получаем следующую задачу финитного управления. Необходимо найти такую финитную функцию U(t), интегрируемую с квадратом, на носителе [-τ, τ], чтобы система (4) перешла из начального состояния (5) в конечное состояние (6), т.е. в начало координат фазового пространства. Число τ будем рассматривать как заданное число.

Следуя методу, предложенному А. Г. Бутковским [2], применим преобразование Фурье к системе (4) с начальным условием (5). Получим выражение

, (7)

решая которое относительно , будем иметь:

                                                                (8)

где Di(ω) — матрица, присоединенная к матрице (jωE – Ai); E — единичная матрица;  — определитель матрицы (iE – Ai).

В соответствии с теоремой Винера-Пэли известно, что для того, чтобы у(t) была финитной функцией, необходимо чтобы правая часть выражения (8) могла быть продолжена на всю комплексную плоскость как целая функция, т. е. функция комплексного переменного

                                                                        (9)

не должна иметь особенностей для любого конечного z. Это приводит к тому, что числитель дроби (9) должен иметь те же нули и той же кратности, что и полином . Пусть полином  имеет корни z1, … , zn. Тогда должны иметь место следующие равенства:

D(zi) [Bi u(zi) + y0] = Di= 1,…, n.                                               (10)

Поэтому для искомой функции u(z) должны выполняться следующие условия:

, i=1,…, n.                                                              (11)

Условия (11) удобно интегрировать, как интерполяционные. Для решения интерполяционной задачи воспользуемся формулой Лагранжа. Пусть корень zk полинома  имеет кратность lk, k=1,…,s. Очевидно, что . Тогда для того, чтобы у(z) было целой функцией, необходимо, и достаточно, чтобы не только числитель обращался и нуль в точке z = zk , но и все его первые производные до (lk— 1) включительно. В этом случае формула Лагранжа, дающая решение интерполяционной задачи, имеет вид:

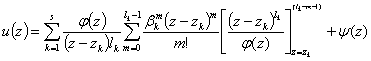.                                 (12)

где m = 0, 1, … , lk -1, k = 1, 2, 3, … , s; ϕ(z) — произвольная целая функция; (z) – целая функция степени τ, обращающаяся в нуль в узлах интерполяции вместе с первыми производными, до(lk - 1)–й.

Для определения искомого финитного управления на носителе ) остается отыскать функцию ϕ(z), удовлетворяющую условиям:      

1)                ϕ(zi) = 0, ϕ’(zi) = 0, …,

2)              

3)               cтепень (z) равна τ.

По теореме Вейерштрасса всякую целую функцию ψ(z) можно представить в виде:

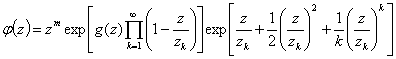                                                      (13)

где m — кратность нулевого корня; zi . . . ,zk — не равные нулю простые корни.

Взяв обратное преобразование Фурье от выражения (12) и выделив вещественную часть, найдем искомое управление:

                                                    (14)

А. Г. Бутковский [2] показал, что управление (14) при  решает задачу оптимального управления в смысле минимума следующего критерия

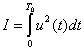.                                                                                              (15)

Поскольку  является произвольной целой функцией, то нет принципиальных трудностей в выборе в классе заданных функций таких и , удовлетворяющих условиям (1-3), которые будут давать минимум выбранного функционала.

Полученное управление u(t) является функцией координат фазового пространства

, т.е.

,                                                                              (16)

.

Поэтому нашей второй задачей является такое определение величины (i Т0), которое обеспечило бы минимум некоторого функционала I на интервале [0, Т] при управлении на каждом подынтервале [i Т0 (i+1)… Т0] типа (16), т. е. требуется найти точки , . Поскольку , т. е. ограничено, то значения х (iT0) тоже ограничены.

Для решения этой задачи разобьем интеграл (2) на сумму п интегралов:

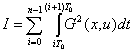, i=0,1…n-1.                                                              (17)

Каждое слагаемое в выражении (17) при известном управлении u(t) зависит только от значений  и .Таким образом, функционал I является функцией от значений , т.е. имеем задачу нахождения экстремума функций (n-1) переменных:

                                                                        (18)

При условии ,                                                    (19)

Эта задача относится к классу задач нелинейного программ программирования с краевыми условиями (19), решение которой можно осуществить известными методами.

Таким образом, решив оптимизационную задачу (18) совместно с определением управления (16), находим решение поставленной задачи оптимального управления объектом на интервале (0, Т) с фиксированными краевыми условиями.

 

ЛИТЕРАТУРА

1. Красовский Н. Н. Теория управления движением. М, «Наука», 1968, 325 с. с ил.

2. Бутковский А. Г. Методы управления системами с распределенными параметрами. М, «Наука», 1975. 669 с. с ил.

3. Системы оптимального управления сложными технологическими объектами/ З. Г. Салихов, Г. Г. Арунянц, А.Л. Рутковский.- М.: Теплоэнергетик, 2004. – 496 с.