V. A. Lebedev

 

Kutateladze Institute of Thermophysics SB RAS Novosibirsk, Russia

 

V.P.Soloviev

 

Birgham Young University Provo, UT, USA

 

SUPPORTING DATA OF VIEW FACTORS FOR CYLINDRICAL SPIRALING TAPES

 

An expanding scope of engineering problems related to the radiation heat transfer poses the problems of determining the fraction of ray energy emitted from the radiating surface i and reaching the irradiated surface j. This implies the need for improving the methods of obtaining the geometric invariants of radiation - the radiation configuration factors (RCFs)  and the mutual surfaces of the radiating surface including the corresponding RCFs.


At present one can cite only two reference works1,7 and the monograph9, which give information about the RCFs for various radiating systems at the level acceptable from the viewpoint of engineering practice. Before the handbooks1,7 were published the data on the RCF analytic and numerical forms for specific configurations of emitting systems were presented in a broader manner than in other works, and still insufficiently completely, in the monograph8. In the above works as well as in the periodical scientific and technical literature there is, however, no information about the diversity of kinds of radiating systems for which there had been the computed results for RCFs in the analytic or graphical forms. For example, the spiral and helical radiating systems belong to almost unexplored objects. The latter systems are dealt with in the only work10, where the Moebius band RCFs were computed.

The work6],which is a further development of work5, the problem is posed on the analytic estimation, in the first approximation, of the RCFs for the spiral radiating systems with a filament of arbitrary cross section.

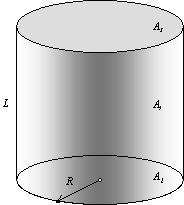
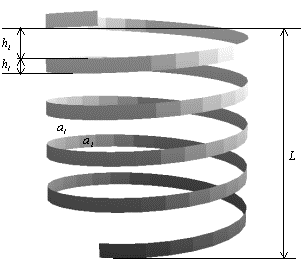
We now proceed to the consideration of a planar cylindrical spiral formed by an infinitely long band of constant width, which is “rolled up” on an imaginary cylinder of radius R. In paper6 various view factors of the spiral are discussed. The case of a long spiral when L >> R  is the most intriguing for practice. By virtue of the closure and symmetry of the system the self-irradiated surface  of the cylindrical flat spiral takes a part (fraction) of the lateral inner surface  of the cylinder used for the construction of the emitting and self-irradiated system in the following proportion: /A= /H. 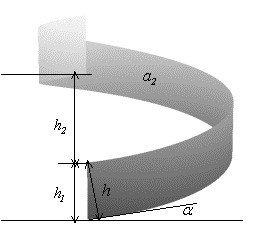Here H is the flank pitch of the spiral,  is the width of the emitting band of the spiral measured in the direction parallel with the symmetry axis of the system:  = h/cosα  (h is the emitting strip width (the spiral band width measured along a normal to the band edges), α is the inclination angle of the spiral turn). It follows from here that /= / = /H, and the RCF for the self-irradiation of spiral is

 = h[1 – 2A(1 – )]/(Hcosα)

Here are some from the former fastors and auxiliary formulas proposed by V.P.Soloviev (University Provo, UT, USA) and facilitate the necessary calculations.

 

View Factors of Cylindrical Spiral Surfaces

 

 

1)      Right Circular Cylinder

 

                  

                 

 

View Factor (disk A2 to parallel coaxial disk A3 of the same radius R) 2:

        

         , where   .

 

2)      Tape of thickness h is rolled around a cylinder: 

          is the area of the lateral surface of the cylinder not covered by the tape;

          is the area of the interior surface of the tape,  .

The interior surface of the tape  is defined parametrically by

 


                  

 

                                              ,  , 

           where

 


                                     

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

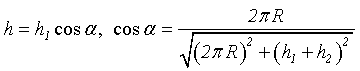
3)  View Factors of the finite spiral :

 

 

                     

               

                                                                

        

                                             

        

        

             

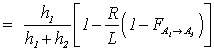
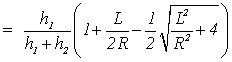
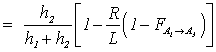
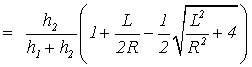
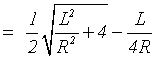
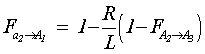
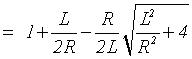
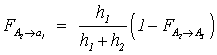
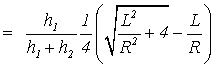
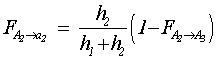
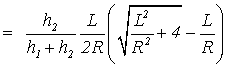
4)      The case of the infinitely long spiral

                   

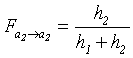
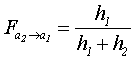
References

1. Howell, J.R., A Catalog of Radiation Configuration Factors, McGraw - Hill Book Co., New York, San Francisco, Toronto, 1985.

2. Howell, J.R., Siegel, R., Mengüç, M.P.: Thermal Radiation Heat Transfer, 5th Edition, CRC Press. 2011. Appendix C-10.

3. Lebedev, V.A, Invariance of radiation shape factor for certain radiating systems, Izv. SO AN SSSR, Ser. Techn. Nauk, n. 13, iss. 3, pp. 73 - 77, 1979.

4. Lebedev, V.A, About relationships between radiation configuration factors for cylindrical emitting systems, Soviet Journal of Applied Physics, Vol. 11, n. 3, pp. 12 - 16, 1988.

5. Lebedev, V.A.: Radiation Configuration Factors for a Flat Cylindrical Spiral,

Thermophysics and Aeromechanics, vol.7, No.3, pp.447-450, 2000.

6. Lebedev, V.A.: Geometric Invariants of Radiation of Spiral Heaters,

Thermophysics and Aeromechanics, vol.10, No.1, pp.101-108, 2003.

7. Rubtsov N.A. and Lebedev, V.A, Geometric Invariants of Emission, Inst. of Thermophys, SB RAS, Novosibirsk, 1989.

8. Siegel R. and Howell, J.R.Thermal Radiation Heat Transfer, McGraw - Hill Book Co., New York, San Francisco, Toronto, 1972

9. Siegel R. and Howell, J.R., Thermal Radiation Heat Transfer, McGraw ¾ Hill Book Co., New York, San Francisco, Toronto, 1972

10. Stasenko. A.L., The self-radiation of Moebius band with a fixed shape, Izv. AN SSSR, Ser. “Energetika i Transport”, n. 4, pp.104 - 107, 1967.