Student Myshko V., Ph.D. Kovalenko M.

National Technical University of Ukraine «Kyiv Polytechnic Institute», Ukraine

MATHEMATICAL MODELING OF ELECTROMAGNETIG FIELDS OF THE ELECTRICAL MACHINES

There are several ways to compute electromagnetic forces. In the most general case, the calculation of electromagnetic forces involves the computation of volume forces acting on a body, and of surface forces originating from jumps in the electromagnetic fields on the boundaries. The volume and surface forces are derived from a general stress tensor that includes electromagnetic terms.

Calculating forces in moving objects is important, especially for electric motors and other moving electromagnetic devices. When performing the computations in a coordinate system that moves with the object, the electromagnetic fields are transformed. The most well-known relation for moving objects is the one for the electric field. The transformed quantity of the electric field is called the electromotive intensity.

Assume that the object modeled is moving with a constant velocity, . The equations now take on a slightly different form that includes the Galilei invariant versions of the electromagnetic fields. The term Galilei invariant is used due to the fact that they remain unchanged after a coordinate transformation of the type:

(1)

In continuum mechanics, this transformation is commonly referred to as a Galilei transformation.

The Galilei invariant fields of interest are [1]:

(Electromotive intensity) (2)

(Free conduction current density) (3)

(Lorentz magnetization) (4)

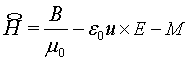(Magnetomotive intensity) (5)

The electromotive intensity is the most important of these invariants. The Lorentz magnetization is significant only in materials for which neither the magnetization M nor the polarization P is negligible. Such materials are rare in practical applications. The same holds for the magnetization term of the magnetomotive intensity. Notice that the term is very small compared to except for cases when and E are both very large. Thus in many practical cases this term can be neglected.

The stress tensor in the surrounding air or vacuum on the outside of a moving object is [2]:

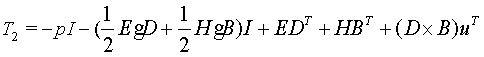(6)

There is an additional term in this expression compared to the stationary case.

The stress tensor in a moving elastic pure conductor is:

,

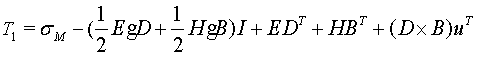where and . (7)

To get the equation for the balance of forces the divergence of this expression needs to be computed. This requires an introduction of an extra term in Cauchy’s equation corresponding to an additional electromagnetic contribution to the linear momentum. Cauchy’s equation with this extra term is [2]:

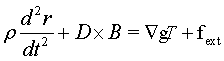(8)

The extra term is canceled out by the additional term in the stress tensor, and the final result is:

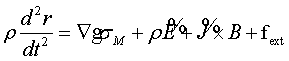(9)

For the case of no acceleration, with the explicit appearance of the transformed quantities:

(10)

The terms containing cancel out, which yields the following equation:

(11)

which is the same expression as for the stationary case.

The stress tensor for a moving general elastic material is [3]:

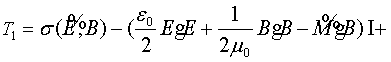
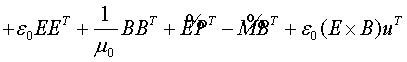(12)

The magnetization M and the polarization P occur explicitly in this expression. To instantiate the stress tensor for the general elastic case a material model explicitly including the magnetization and polarization effects is needed.

Thus, this method allows to сalculating forces in moving objects, especially in electric motors and other moving electromagnetic devices.

References:

1. A. Kovetz, The Principles of Electromagnetic Theory, Cambridge University Press, 1990.

2. O. Wilson, Introduction to Theory and Design of Sonar Transducers, Peninsula Publishing, 1988.

3. D.K. Cheng, Field and Wave Electromagnetics, 2nd ed., Addison-Wesley, 1991.