Student Pavlovska K., Ph.D. Kovalenko M.

National Technical University of Ukraine «Kyiv Polytechnic Institute», Ukraine

OVERVIEW OF FORCES IN CONTINUUM MECHANICS

All variety of naturally occurring interactions is reduced to only four types. This gravitational electromagnetic, nuclear and weak interactions. In Newtonian mechanics can be considered only gravitational and electromagnetic interactions. In contrast to the short-range nuclear and weak interactions, the gravitational and electromagnetic interaction - the long-range: their actions are manifested at very large distances.

The main provisions of continuum mechanics, playing a role of axioms, or the most important theorems:

1. Euclidean space. The space in which the motion of the body - three-dimensional Euclidean point space.

2. Absolute time t. The passage of time does not depend on the choice of the reference system.

3. The hypothesis of continuity. Material body - continuous medium.

4. The law of conservation of mass. Any material body V has a scalar non-negative characteristic - mass M, which: a) is not changed by any movements of the body, if the body is composed of the same material points, b) an additive value.

5. The law of conservation of momentum (change in momentum).

6. The law of conservation of angular momentum (change of angular momentum).

7. The law of conservation of energy (first law of thermodynamics).

8. The existence of absolute temperature (zero law of thermodynamics).

9. The law of entropy balance (the second law of thermodynamics).

Cauchy’s equation of continuum mechanics reads

(1)

where is the density, denotes the coordinates of a material point, is the stress tensor, and is an external volume force such as gravity (). This is the equation solved in the structural mechanics physics interfaces for the special case of a linear elastic material, neglecting the electromagnetic contributions.

In the stationary case there is no acceleration, and the equation representing the force balance is

(2)

The stress tensor must be continuous across a stationary boundary between two materials. This corresponds to the equation

(3)

where and represent the stress tensor in materials 1 and 2, respectively, and is the normal pointing out from the domain containing material 1. This relation gives rise to a surface force acting on the boundary between material 1 and 2.

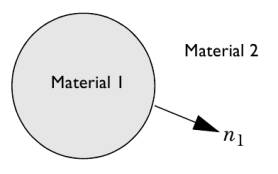
Fig.1 The stress tensor in materials 1 and 2

In certain cases, the stress tensor T can be divided into one part that depends on the electromagnetic field quantities and one part that is the mechanical stress tensor,

(4)

For the special case of an elastic body, the mechanical stress tensor is proportional only to the strain and the temperature gradient. The exact nature of this split of the stress tensor into an electromagnetic and a mechanical part depends on the material model, if it can be made at all.

It is sometimes convenient to use a volume force instead of the stress tensor. This force is obtained from the relation

(5)

This changes the force balance equation to

(6)

or, as stated in the structural mechanics physics interfaces,

where (7)

In continuum mechanics techniques developed mechanical problems to the attention of mathematics, that is, to the problem of finding some numbers or numeric functions using various mathematical operations. In addition, an important goal of continuum mechanics is to establish the general properties and laws of motion of deformable bodies and force interactions in these bodies.

Under the influence of continuum mechanics received a large number of developing branches of mathematics - for example, some sections of the theory of functions of complex variable boundary value problems for partial differential equations, integral equations, and others.

References:

1. B.D. Popovic, Introductory Engineering Electromagnetics, Addison-Wesley, Reading, Massachusetts, 1971

2. R.K. Wangsness, Electromagnetic Fields, 2nd ed., John Wiley & Sons, 1986

3. A. Kovetz, The Principles of Electromagnetic Theory, Cambridge University Press, 1990