К.т.н., доцент Шаров. В.В., аспирант Антонов К.А.

Казанский Государственный Энергетический Университет, Россия

Система мониторинга сопротивления изоляции электрических машин по температуре статорных обмоток

При эксплуатации электрических машин (ЭМ) в реальных условиях температура статорных обмоток в зависимости от нагрузки в рабочем режиме изменяется. Это обстоятельство приводит к тому факту, что при изменении температуры изменяется и величина сопротивления изоляции. Практика показывает, что величина сопротивления изоляции уменьшается в 2 раза при повышении температуры на каждые Δθ °С [1].

Схема экспериментальной установки для контроля температуры статорных обмоток ЭМ без вывода ее из эксплуатации представлена на рис.1.

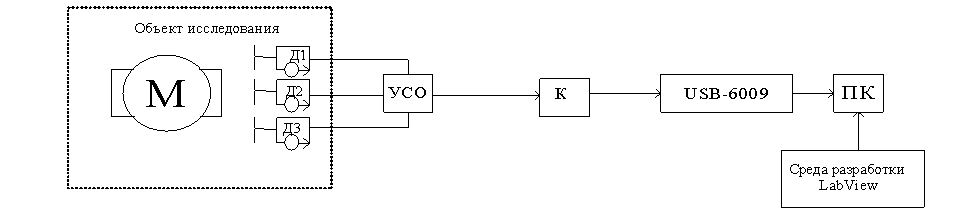
Рис. 1. Схема экспериментальной установки

В состав экспериментальной установки входят: трехфазный асинхронный двигатель, три датчика температуры DS18B20, устройство связи с объектом, коммутатор, интерфейс USB-6009, персональный компьютер (ПК) и среда обработки и визуализации данных LabVIEW.

Стандарты на ЭМ оценивают тепловое состояние машины не по температуре ее частей, а по превышению их температуры над температурой охлаждающей среды, которая для нормальных условий эксплуатации принята равной 40°С.

Для определения величины сопротивления изоляции ЭМ по температуре статорных обмоток ЭМ имеются математические уравнения взаимосвязи [1..3].

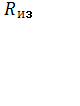Величина сопротивления изоляции ЭМ в условиях эксплуатации может быть определена следующим образом. Зная величину сопротивления изоляции при температуре , которая определяется при 20⁰ С, можно определить величину сопротивления изоляции при температуре θэ на основании соотношения

. (1)

Исходя из полного тока через диэлектрик, имеющего потери релаксационные и сквозной проводимости, получим тангенс угла потерь

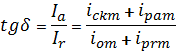, (2)

где все токи имеют амплитудные значения: – ток сквозной проводимости, – безынерционный ток смещения, и – активная и реактивная составляющие релаксационного тока поляризации.

Подставив в уравнение значения токов (2), выраженных через параметры изоляции, получим соотношение

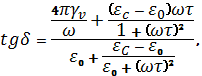(3)

где – удельная объемная электропроводность диэлектрика; , – статическая (при постоянном токе) и динамическая (при высоких частотах) диэлектрические проницаемости диэлектрика; – постоянная времени релаксации диэлектрика.

При очень низких частотах основными являются потери энергии сквозной проводимости

. (4)

На постоянном токе , tgδ →0, и потери сквозной проводимости получаются равны

, (5)

где S – площадь проводящей части обмотки; d – толщина изоляции.

Для диэлектриков с релаксационной поляризацией и малой величиной на высоких частотах основную роль играют релаксационные потери, поэтому слагаемым, содержащим можно пренебречь, и тогда получаем соотношение

. (6)

С повышением частоты, т.е. с увеличением ωτ, tgδ вначале растет при малых значениях ωτ, а затем убывает, проходя через максимум. Таким образом, зависимость имеет две составляющие для диэлектриков с релаксационной поляризацией: потери на сквозную проводимость, которые убывают с ростом ωτ и дипольно-релаксационные потери, которые имеют максимум.

Время релаксации поляризации r уменьшается с ростом температуры по экспоненциальной зависимости на основе соотношения

, (7)

где – постоянная времени; К – постоянная Больцмана; Т – температура.

Температурно-частотные зависимости отражают физико-химические свойства диэлектрика, его структуру. Внешние воздействия на диэлектрик эксплуатационных факторов (температуры, влажности, механических напряжений, электрического поля) вызывает структурные изменения диэлектрика, что также отражается на зависимостях .

Литература

1. Готтер Г. Нагревание и охлаждение электрических машин. – М.:-Л.: Госэнергоиздат, 1961. – 264 с.

2. Гуревич Э.И., Рыбин Ю.Л. Переходные тепловые процессы в электрических машинах. – Л.: Энергоатомиздат, 1983. – 216 с.

3. Гуревич Э.И. Тепловые испытания и исследования электрических машин. Л.: Энергия, 1977. – 216 с.