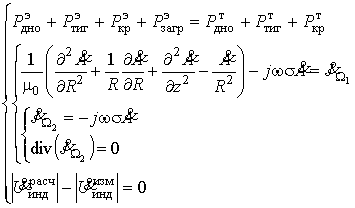Шатунов А.Н., Максимов А.И, Кичигин В.В.

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ», Россия

Удельное сопротивление высокотемпературного
расплава системы Al2O3–ZrO2

Материалы на основе оксидной керамики непрерывно совершенствуются. В основу разработки технологии синтеза циркониево-алюминиевой керамики с субмикронной структурой легло наличие области фазового разделения в расплавах системы Al₂O₃–ZrO₂ [1], которая находится в диапазоне температур 2050°C-2500°C. Получение данного типа материалов требует фиксирования структуры расплава путем острой закалки. Для осуществления этого процесса производится непрерывная плавка оксидной смеси заданного состава в индукционной печи с холодным тиглем, доведение расплава до необходимой температуры и непрерывная разливка расплава в закалочную установку с получением закаленной структуры с мелкодисперсной фазой, образованной вследствие неравновесной кристаллизации при быстром охлаждении. Изделия, изготовленные из прекурсоров с такой структурой, обладают более высокой твердостью, прочностью и стойкостью к перепадам температур. Однако отсутствие достоверных данных об удельном электрическом сопротивлении оксидных расплавов с заданным содержанием компонентов при высоких температурах усложняет разработку технологий непрерывной разливки и проектирование энергоэффективных индукционных систем для их реализации. Поэтому требуется определение удельного сопротивления расплава Al₂O₃–ZrO₂.

В основе используемого метода лежит незагрязняющий способ плавки в разрезном проводящем тигле, измерение тепловых и электрических параметров индукционной системы и решение обратной задачи электромагнитного поля. Обратная задача решается относительно удельной электропроводности расплава . Система уравнений включает уравнение электромагнитного поля и условие баланса мощностей, обеспечивающие её решение:

(1)

где  – электрические потери в дне разрезного водоохлаждаемого тигля, секциях тигля, крышке тигля и расплаве соответственно; , ,  – суммарные мощности, отводимые от дна, секций и крышки тигля соответственно, включающие собственные электрические потери и тепловые потери от расплава.

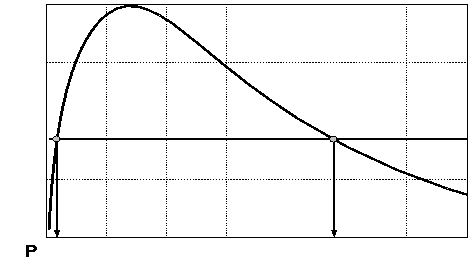
Графическая интерпретация решения обратной задачи представлена на рисунке 1. В постановке на основе баланса мощностей (1) для обеспечения однозначности решения (точки 1 или 2) необходимо ввести дополнительное условие, основанное на измерении и расчёте напряжения на индукторе .

2

Рисунок 1 – Решение обратной задачи в постановке на основе

баланса мощностей

Исходные данные для баланса мощностей измеряются в ходе натурных экспериментов на исследовательском стенде (рисунок 2). В состав стенда входят: транзисторный генератор, индукционная печь с разрезным водоохлаждаемым тиглем и система сбора данных.

Г

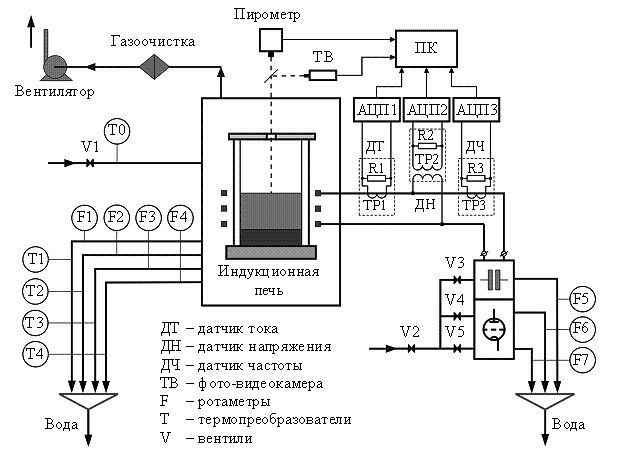
Рисунок 2 – Структурная схема исследовательского стенда

С использованием рассмотренного метода было определено удельного сопротивления расплава оксидной системы с составом 58%Al₂O₃ – 42%ZrO₂ (масс.) в интервале температур 2140÷2280°С при плавке на воздухе. Данные измерений и результаты расчетов приведены в таблице.

Таблица – Результаты измерений и расчетов
Основные размеры индукционных систем, см		, °C	, кГц	, кВт	, В	, кВт	, Ом∙м	, ±%
		Измерение					Расчёт
Hинд = 25.0 Rинд = 17.0	Hраспл= 22.5 Rраспл = 12.9	2276	280.7	104.2	753.0	4.20	0.98×10^-2	14
	Hраспл= 10.0 Rраспл = 12.9	2277	309.5	90.92	744.2	2.64	0.70×10^-2	21
	Hраспл= 18.0 Rраспл = 12.9	2275	295.0	70.67	756.6	2.12	0.90×10^-2	16
	Hраспл= 18.0 Rраспл = 12.9	2144	297.0	88.05	815.5	2.53	1.20×10^-2	15

где H_инд – высота индуктора; R_инд – внутренний радиус индуктора; H_распл,
R_распл – высота и радиус ванны расплава соответственно; Т_распл – температура на поверхности расплава;  – потери в индукторе;  – напряжение на индукторе;  – погрешность определения удельного сопротивления.

Полная погрешность метода вычисляется как сумма погрешности решения обратной задачи и погрешности численной математической модели электромагнитного поля по методике, рассмотренной в [2]. При уменьшении соотношения высоты расплава к высоте индуктора (эксперимент при температуре 2277°С) погрешность метода увеличивается. Ее типичное значение для рассматриваемой системы при работе на неярком поверхностном эффекте составляет порядка 15%.

Список литературы

1. Исследование закалки образцов из расплава системы Al2O3–ZrO2 / Шатунов А.Н. и др. // Известия СПбГЭТУ. – С.–Петерб., №5, 2008.– С. 29-32.

2. Method of electrical resistivity measurement for high-temperature melts / A.N. Shatunov, A.I. Maksimov, A.Yu. Pechenkov, I.V. Poznyak // Inorganic Materials, 2011, Vol. 47, No. 14, pp. 1579-1583.