MEL’NICK V.M.

NATIONAL TECHNICAL UNIVERSITY OF UKRAINE "IGOR SIKORSKY KYIV POLYTECHNIC INSTITUTE"

ERRORS OF STABILIZATION

Linear approximation

; ;

; ; (1)

; .

Here – linear approximation solutions which did not take into account the nonlinear members - gyroscopic moments of cross-links; – addition to the solutions relatively the first, etc. order infinitesimality.

With the rejection of nonlinear members , , , the equation of the system (6.1) can be regarded as pairs of equation of three independent stabilization systems under the influence of disturbances and . The reaction of these disturbances is the solution of the linear approximation and .

After substituting of the expressions into the equation (6.1), we again obtain the linear equations, but relatively to variable and , structurally similar to the equations of linear approximation, although in the right sidewill be already present , and .

Assuming that the values and much smaller than the corresponding solutions of linear approximation, we can write down –

;

;

. (2)

Thus, the task of finding the solutions of the first approximation is reduced again to determinition of the reactions of two independent linear systems of perturbation and , caused by the cross impact of the stabilization channels.

Similarly, if necessary, we can find the second, third, etc. the following approximation.

The first four equations of the system can be solved independently of the latter two, so we will continue to analyze the system from the first four equations without studying of the GSP dynamics as a closed system. We conditionally assume the circles of stabilization as opened, however, we consider the platform small oscillations relatively to the axes, , , which are responsible for stabilization errors.

In the linear approximation equations the two channels of stabilization fall into the following two subsystems which are not connected –

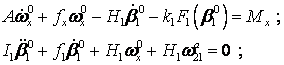(3)

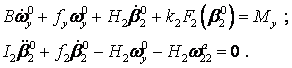(4)

The reaction of GSP on periodic perturbations will contain forced and own oscillations. We assume that the latter ones will quickly die down.

Then the solutions of the systems (3) and (4) at the harmonic perturbations are easily obtained using the frequency chracteristics of the system:

; ;

; , (5)

where, , , – respectively the amplitude-frequency characteristics and phase-frequent characteristics of the tract between the input influence and the original value; ; .

The structural schemes of the platform in the linear approximation are shown in Fig. 1. Their corresponding transfer functions of the platform are outlined by the correlations –

; ;

; ;

;

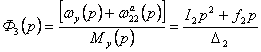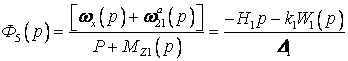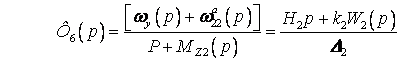, (6)

Where

(7)

From the expression (6.11) it follows, that the constant components of angle rate and are not shown by linear approximation.

Estimation of the stabilization error in the first approximation. Now we consider the first approximation. Substituting (1), and taking into account (3) and (4), we obtain a system of linear equations, where and are determined by the expressions (2):

;

;

;

. (8)

Substituting in the expression (2) the solution (1) we find:

;

.

Elementary transformations make possible to write these correlation as follows –

;

. (9)

Perturbations of the sensstive GSP elements on the precession axis will be the periodic moments-obstacles of different and total frequencies. Consequently, the reaction of these perturbations platform will have the same structure (2, а).

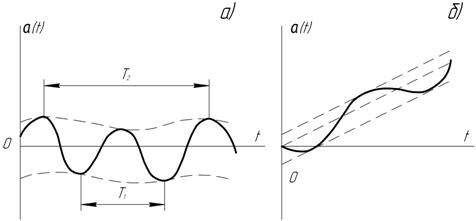Fig. 2. Changes of inclination angles of the gyrostabilizer platform at different frequencies of exciting: а) б)

At the frequencies equality, in other words, when , the expression (9) changes –

;

.

Obviously, there are constant components of exciting moments relatively to the output axis of gyroblocks –

;

. (10)

These constant components cause the systematic drift of the platform relatively to the axes of stabilization with the angle rate

;

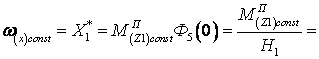
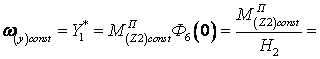
. (11)

The character of the GSP movement when is shown in Fig. 2, б. Obviously, the acoustic vibration of the surface float gyroscopic sensitive elements, with a wide frequency range, will contain in the values , the components of the frequencies of the kinematic perturbation base. Thus, there will be a selectivity of these variables and a systematic drift of the platform will also contain the value of pressure of sound radiation . The frequencies, which do not match, will enrich the range of harmonic components [1-3].

If the difference between the frequencies and is large, the GSP errors have the oscillation origin of different oscillation and total frequencies. When they are getting close to each other, except the long periodic and short periodic components may occur beating.

At synchronous tossing the GSP has a systembothatic drift around all three axes of stabilization. Their value depend on the origin of the perturbation and parameters of the platforms which are contained in amplitude-frequent and phase-frequent characteristics, as well as in values of the phase shift.

The estimation of the second approximation generates the confidence to believe that it’s enough to consider only the first approximation.

The research has proven the following: at the fuselage tossing, the GSP gyroscopic sensitive elements in the acoustic fields of a supersonic flight have the errors of measurement, which cause the construction errors of tryorthohonal coordinate system for the aircraft; it is clarified the structure of construction errors in the coordinate system using GSP, which enables to estimate the degree of influence of kinematic and acoustic perturbations; it is opened the mechanism of diffraction of sound waves in mechanical impedance systems of the gimbal in the inertial devices; the results obtained may serve as a theoretical basis of improvement the accuracy of constructing the guide lines for hypersonic vehicles of different classes.

References

1. Mel'nik, V.N. Stress-strain state of a gyroscope suspension under acoustic loading [Текст]/ V.N. Mel’nik // 2007; Strength of Materials. ISSN: 00392316. Volume: 39. Issue: 1. Pages: 24-36. Year: 2007-01-01. EID: 2-s2.0-34147198666. Scopus ID: 34147198666. DOI: 10.1007/s11223-007-0004-6.

2. Mel'nik, V.N. Influence of acoustic radiation on the sensors of a gyrostabilized platform [Текст]/ V.N. Mel’nik, V.V. Karachun// 2004; Prikladnaya Mekhanika. ISSN: 00328243. Volume: 40. Issue: 10. Pages: 122-130. Year: 2004-12-01. EID: 2-s2.0-14844342416. Scopus ID: 14844342416.

3. Mel'nick, V.N. Determining Gyroscopic Integrator Errors to Diffraction of Sound Waves [Текст] / V.N. Mel'nick, V.V. Karachun // International Applied Mechanics. -2004. –T. 40(3). – P. 328-336.

4. Karachun, V.V. Vibration of Porous. Plates under the Action of Acoustic [Текст] / V.V. Karachun // SOVIET APPLIED MECHANICS. – 1987. – Vol. 22, №3. – Р. 236-238.