Современные информационные технологии/3. Программное обеспечение

К.т.н. Удовик И.М.

ГВУЗ «Национальный горный университет»

Программное обеспечение обработки слабоконтрастных изображений в пространстве элипсометрических

параметров Стокса.

Возможность создания виртуального аналога эллипсометрических методов основана на свойствах поляризованной электромагнитной волны. Известно, что электрический вектор Е= соответствует волне, в комплексном представлении описываемой выражением [1]

Е , (1)

где – циклическая частота, – волновое число ( – длина волны оптического излучения), – амплитуды ортогональных составляющих. Тогда в каждой точке пространства вектор Е описывает замкнутую кривую, являющуюся эллипсом, уравнение которого имеет вид [2,3]

, (2)

где ; ; Если и , то эллипс вырождается в окружность (круговая поляризация), а если , то он вырождается в прямую линию (линейная поляризация).

Таким образом, поле в каждой точке характеризуется плоскостью, в которой лежит его эллипс поляризации, который может быть полностью охарактеризован параметрами Стокса определяемыми как [86]

; ; (3)

Параметр пропорционален интенсивности анализируемого изображения, а можно интерпретировать как декартовы координаты точки на сфере радиусом , известной как сфера Пуанкаре.

Структура алгоритма для реализации виртуального эллипсометрического метода для обычных (однопараметровых) изображений включает в себя следующие этапы.

1. Модуляционное преобразование исходного изображения

(4)

позволяет сопоставить каждому пикселю анализируемого изображения две ортогональные компоненты векторного поля – действительная и мнимая части выражения

,

которые интерпретируются в виде аналога ортогональных составляющих и , соответственно.

2. Фазовая компонента вычисляется на основе использования аналога выражения, т.е.

, (5)

где H – оператор эквализации гистограммы исходного изображения , – стабилизирующий параметр (выбирался равным 0.001).

3. Синтез четырех эллипсометрических характеристик и исходного изображения на основе использования выражения (3) .

4. Визуализация и анализ новых виртуальных изображений, полученных на основе эллипсометрических характеристик.

На рис. 1 представлено окно работы системы InterferenseImageProcessing для обработки слабоконтрастных изображений в рамках метода виртуальной цифровой эллипсометрии.

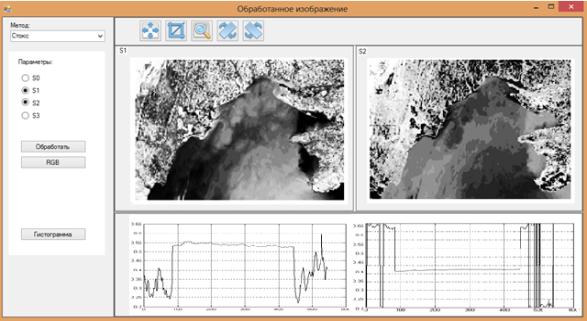
Рис. 1 Обработка слабоконтрастного изображения

на основе параметров Стокса

На примере окна системы, представленного на рис. 4.18, показан пример обработки слабоконтрастного изображения акватории Черного моря на основе метода виртуальной цифровой интерферометрии с выводом информативных параметров Стокса S₁ и S₂. Система позволяет осуществлять RGB-кодирование на основе комбинаций параметров Стокса (рис. 2).

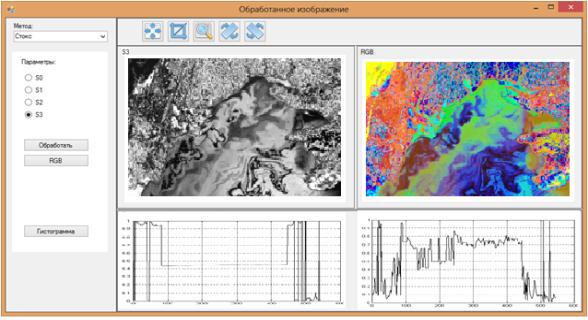
Рис. 2. Окно RGB-кодирования на основе комбинаций

параметров Стокса

Имеется возможность одновременного вывода исходного и обрабатываемого изображения в уровнях серого и псевдокодировании, построения графиков яркостно-пространственных срезов, формирование окон из части изображения с дальнейшим его исследованием.

Система InterferenseImageProcessing позволяет также осуществлять масштабирование, поворот изображения и обрезку участков.

Программное обеспечение для анализа слабоконтрастных изображений в пространстве эллипсометрических параметров Стокса может быть применено для повышения чувствительности, как однопараметровых, так и многопараметровых изображений.

В рамках метода каждому пикселю анализируемого изображения сопоставляется четыре виртуальных параметра Стокса, что позволяет естественным способом осуществлять цветовое RGB кодирование результатов, без использования процедуры псевдоцветового кодирования.

Предложенный способ интерпретации результатов с использованием RGB кодирования на основе параметров способствует повышению достоверности анализа слабоконтрастных изображений.

Литература:

1. Конев В.А. Радиоволновая эллипсометрия / В.А. Конев, Е.М. Кулешов, Н.Н. Нунько – Минск: Наука и техника, 1985. – 184 с.

2. Аззам Р. Эллипсометрия и поляризованный свет / Р. Аззам, Н. Башара; под ред. А.В. Ржанова., К.К. Свиташева. – М.: Мир, 1981. – 583 с.

3. Основы эллипсометрии / [под ред. А.В. Ржанова]. – Новосибирск: Наука, 1979. – 422 с.