Евсеев В.И.,

канд. физ.-мат. наук, доцент, г.Казань, РТ, Россия

Изучение формул пентарных фигур

Аннотация:

В этой заметке продолжается изучение логических формул применительно к случаю, когда они состоят из пяти квадратных, соединенных ребрами клеток.

Рассмотрены все двенадцать исходных позиций этих фигур, взятых из основного полигона. Метод получения формул для остальных позиций автором уже указан в одной из публикованных им работ.

Abstract:

in this post continues the study of logic in the case formulas when it is composed of five squares, the edges of the cells. Twelve original all the positions of these figures, taken on the main site. Method to get formulas for the other posts the author already exists in one of his published works.

Как известно, пентарные фигуры (их всего 12) составляют, с одной стороны игру «пентамино», которая известна с середины прошлого века, а с другой стороны, представляют исходные структурные матрицы, которыми можно моделировать клеточное строение материи. Поэтому нам кажется, что увеличение информации о строении и логическом содержании этих матриц вполне своевременно.

Также своевременно, наверное, перейти от малых фигурных комплексов к средним, в которые входят и пентимы, и гексимы, а после начать исследование больших фигур, состоящих из семи и восьми клеток.

Поэтому в данных работах мы последовательно рассмотрим основные случаи для логических формул пентарных фигур. Заметим, что каждую фигуру мы представляем на соответствующем по размерам вмещающем полигоне вместе с ее полной оболочкой.

1. Формулы первой пентимы.

Для первой пентарной фигуры существует только две позиции, поэтому мы получаем две формулы. Первая из них отражает вертикальный случай.

()
						0	1	0
					0	0	0	0
					1	0	1	0
					0	0	1	0
					1	0	1	1
					0	0	1	0
					1	0	1	0
					0	0	0	0

Значит, мы получаем формулу, состоящую из шести линий:

(1а)

данная позиция этим исчерпывается.

Вторая позиция характеризуется транспонированным полигоном и соответствующей матрицей:

()
		0	1	0	1	0	1	0
	0	0	0	0	0	0	0	0
	1	0	1	1	1	1	1	0
	0	0	0	0	0	0	0	0

В этом случае матрица имеет всего две линии, поэтому получаем:

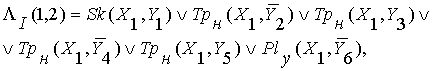(1б)

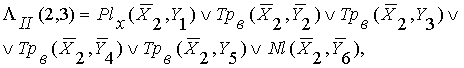
2. Формулы второй пентимы.

Вторая пентарная фигура исходно принадлежит полигону и симметриями не обладает. Для нее получается восемь возможных позиций (с транспонированием полигона) и восемь формул, состоящих из соответственного количества линий.

У этих фигур уже появляются пустые клетки, так как оболочки фигур не совпадают с границами полигона.

Получаем следующую матрицу позиции ():

(а)
				0	1	0	1
			0	Ø	0	0	0
			1	0	0	1	0
			0	0	1	1	0
			1	0	1	1	0
			0	0	0	0	0

Для этой позиции находим линии логической матрицы:

(2)

В дальнейшем в этой заметке мы будем рассматривать только исходные позиции пентарных фигур, так как метод получения остальных позиций описан нами в уже опубликованной статье (см. [3]).

3. Формулы третьей пентимы.

Эта фигура обладает осью симметрии, поэтому она допускает только четыре позиции. Первая позиция () определяется матрицей:

()
				0	1	0	1	0
			0	Ø	0	0	0	Ø
			1	Ø	0	1	0	Ø
			0	0	0	1	0	0
			1	0	1	1	1	0
			0	0	0	0	0	0

В результате находятся четыре логических линии:

(3)

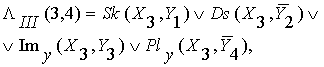
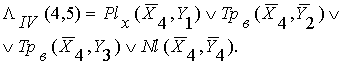
Здесь все позиции расположены на полигоне одного типа и мы не будем их приводить.

4. Формулы четвертой пентимы.

Эта фигура никакими симметриями не обладает, поэтому она имеет восемь различных позиций. Им соответствуют различные логические линии и формулы. Первая позиция () принадлежит полигону .

Она имеет следующую матрицу:

	()
					0	1	0	1
				0	0	0	0	0
				1	0	1	1	0
				0	0	1	0	0
				1	0	1	0	Ø
				0	0	1	0	Ø
				1	0	0	0	Ø

У этой матрицы пять логических линий, которые приводят к формулам:

(4)

Вторая позиция () получается поворотом из первой позиции, поэтому ее полигон становится транспонированным по сравнению с исходным, мы оставляем эту работу для самостоятельного творчества читателей, как и все остальные возможные позиции этой фигуры (их всего восемь).

5. Формулы пятой пентимы.

Эта фигура обладает двумя осями симметрии, поэтому она допускает лишь одну позицию, которую условно обозначим ().

Матрица этой позиции принадлежит полигону :

()
				0	1	0	1	0
			0	Ø	0	0	0	Ø
			1	0	0	1	0	0
			0	0	1	1	1	0
			1	0	0	1	0	0
			0	Ø	0	0	0	Ø

Для нее находим формулы ее четырех логических линий:

(5)

Других позиций у этой фигуры нет.

6. Формулы шестой пентимы.

Исходная позиция этой пентимы принадлежит полигону , причем фигура имеет ось симметрии, поэтому она допускает только четыре позиции, мы будем рассматривать только первую, исходную из них.

Матрица исходной позиции такова:

()
			0	1	0		1		0
		0	0	0	0		0		0
		1	0	1	0		1		0
		0	0	1	1		1		0
		1	0	0	0		0		0

Логические линии здесь получаются следующими:

(6)

Другие три случая здесь не рассматриваются.

7. Формулы седьмой пентимы.

Эта фигура тоже имеет ось симметрии и допускает четыре позиции.

Мы рассматриваем лишь исходную позицию.

():

()
				0	1	0	1	0
			0	Ø	Ø	0	0	0
			1	Ø	0	0	1	0
			0	0	0	1	1	0
			1	0	1	1	0	0
			0	0	0	0	0	Ø

Значит, здесь находим четыре логические линии:

(7)

8. Формулы восьмой пентимы.

()
				0	1	0	1	0
			0	Ø	Ø	0	0	0
			1	0	0	0	1	0
			0	0	1	1	1	0
			1	0	1	0	0	0
			0	0	0	0	Ø	Ø

Это – вид определяющей матрицы.

Их нее получаем формулы четырех логических линий:

(8)

Другие позиции этой фигуры мы здесь рассматривать не будем.

9. Формулы девятой пентимы.

Для этой фигуры в начальной позиции строится определяющая матрица:

()
				0	1	0	1	0
			0	Ø	Ø	0	0	0
			1	0	0	0	1	0
			0	0	1	1	1	0
			1	0	0	1	0	0
			0	Ø	0	0	0	Ø

Таким образом, здесь находятся все логические линии:

(9)

Остальные позиции описываются аналогично согласно таблице.

10. Формулы десятой пентимы.

Здесь находится определяющая матрица

	()
			0	1	0	1	0	1
		0	0	0	0	0	0	0
		1	0	1	1	1	1	0
		0	0	0	0	1	0	0
		1	Ø	Ø	0	0	0	Ø

Отсюда можно построить все три логических линии для этой фигуры.

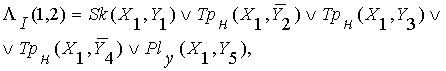(10)

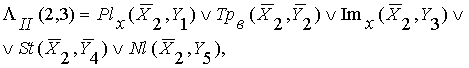
Остальные семь возможных позиций остаются для изучения читателями.

11. Формулы одиннадцатой пентимы.

В этом случае определяется логическая матрица фигуры:

	()
					0	1	0	1
				0	Ø	0	0	0
				1	Ø	0	1	0
				0	0	0	1	0
				1	0	1	1	0
				0	0	1	0	0
				1	0	0	0	Ø

Значит, здесь определяются пять логических линий для формулы этой фигуры.

(11)

11. Формулы двенадцатой пентимы.

Последняя фигура обладает симметрией и поэтому имеет четыре позиции.

Мы рассмотрим, как и в предыдущих случаях, лишь первую из них, а остальные получаются по аналогии.

Эта модель погружается в полигон П(5,5) , поэтому определяющая матрица имеет вид

()
				0	1	0	1	0
			0	0	0	0	Ø	Ø
			1	0	1	0	Ø	Ø
			0	0	1	0	0	0
			1	0	1	1	1	0
			0	0	0	0	0	0

Сразу же записываем четыре формулы для ее логических линий:

Таким образом, мы закончили изучение исходных позиций всех фигур пентарного типа. В дальнейшем мы планируем также рассмотреть основные позиции гексарных (их 35) и септарных ( 107 основных) фигур, а также параллельно изучать фигурные комплексы, содержащие эти типы фигур.

Литература:

1. Евсеев В.И. Конструктивная комплементарная семантика. Монография. Изд – во «Lambert». Германия. 2014.

2. Евсеев В.И. Изучение позиций пентарных фигур// Образование и наука, материалы Х международной научно-практической конференции, т.11. София, «Бял ГРАД-БГ» ООД, 2014, (47 – 63).

3. Евсеев В.И.Позиции и формулы малых логических фигур// Там же, стр. 63 – 72 .