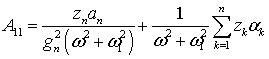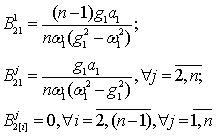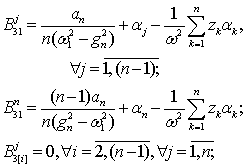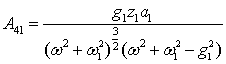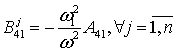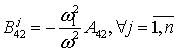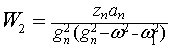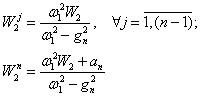Докукова Н.А., Кафтайкина Е.Н., Конон Н.П.
Белорусский государственный университет
СИНХРОННЫЕ КОЛЕБАНИЯ N - АВТОНОМНЫХ ОСЦИЛЛЯТОРОВ
НА ОДНОЙ НЕУПРУГОЙ БАЛКЕ С ЖЕСТКОЙ ЗАДЕЛКОЙ
Введение. Синхронизацией называют подстройку ритмов
автоколебательных систем за счет слабого взаимодействия между ними [1, 2]. В
этом явлении не совсем ясны механизмы проявления тех или иных особенностей
взаимовлияния колебаний осциллирующих элементов, по фазам, частотам,
амплитудам, по влиянию внешних воздействий и факторов на отдельные тела и всю
систему в целом.
В работе представлена общая линейная динамическая модель колебаний
произвольного числа n одинаковых автономных
осцилляторов на рисунке 1, имеющих общую связь – неупругую балку с жесткой
заделкой, записаны уравнения движения (1)-(3), исследованы
особенности и закономерности в представленных математических моделях, изучено
поведение объектов (7)-(11), (12)-(16) с изменяющимися начальными условиями, получены
точные аналитические формулы
(5), (6) и в таблице 1 колебательных режимов (n+1) тел, по
методике, развитой авторами в [3-5], проведены численные расчеты. Результаты
сопоставлены с экспериментальными данными, широко известными в литературе [1, 2].
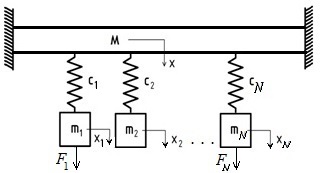
Рисунок 1 - Схема колебаний n - осцилляторов на закрепленной балке с жесткой
заделкой
Постановка
задачи и общий анализ. Система
уравнений движения динамической схемы на рисунке 1 в матричной форме примет
вид:
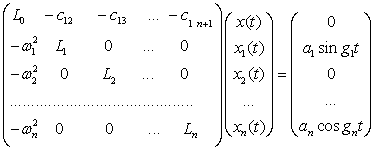 , (1)
, (1)
с начальными условиями
![]() ,
, ![]() , (2)
, (2)
![]() ,
, ![]() . (3)
. (3)
Здесь ![]() ,
, ![]() −
дифференциальные операторы по параметру времени t;
−
дифференциальные операторы по параметру времени t; ![]() ,
, ![]() ;
; ![]() ;
; ![]() ,
, ![]() ; cij – коэффициенты упругих элементов cj-1, отнесенных к соответствующим массам mi-1,
; cij – коэффициенты упругих элементов cj-1, отнесенных к соответствующим массам mi-1, ![]() ;
; ![]() – вектор искомых
перемещений масс на рисунке 1;
– вектор искомых
перемещений масс на рисунке 1; ![]() – вектор виброускорений
нагрузочного режима, а1 =
– вектор виброускорений
нагрузочного режима, а1 = ![]() /m1 , аn =
/m1 , аn = ![]() /mn;
/mn; ![]() и
и ![]() – гармонические силы, являющиеся внешними, приложены к первому
и последнему осцилляторам.
– гармонические силы, являющиеся внешними, приложены к первому
и последнему осцилляторам.
Характеристическое уравнение примет
вид
![]() , (4)
, (4)
если парциальные
частоты всех n линейных осцилляторов одинаковы ![]() ,
, ![]() и
и ![]() . Тогда общие решения многоэлементной динамической задачи
(1)-(3) приводятся к следующим колебательным режимам:
. Тогда общие решения многоэлементной динамической задачи
(1)-(3) приводятся к следующим колебательным режимам:
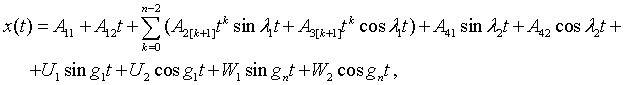 (5)
(5)
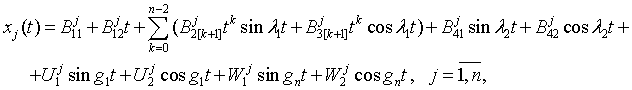 (6)
(6)
где l1=w1, ![]() . Неопределенные коэффициенты соответствующих решений находятся
по методике, развитой в [3], аналитические формулы для которых сведены в
таблицу 1.
. Неопределенные коэффициенты соответствующих решений находятся
по методике, развитой в [3], аналитические формулы для которых сведены в
таблицу 1.
Таблица
1
|
N |
Коэффициенты перемещения балки x(t) |
Коэффициенты
перемещений автономных осцилляторов xj(t), |
|
1 |
2 |
3 |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
5 |
|
|
|
U2 = 0 |
|
|
|
6 |
W1 = 0 |
|
|
|
|
Если положить n=2, с12=с13,
a1=an=0 и выбрать в качестве
начальных условий a1=g , a2=d, то получаются аналитические
формулы решений, полностью совпадающие с
перемещениями в [5].
В качестве
примера рассмотрим механизм с произвольными физическими параметрами: n = 4, M = 20.0 кг, m1=m2=m3=m4= 2.0 кг, c1=c2=c3=c4= 55.0н/м,
a1=0.008 м, a2 = -0.01 м, a3 = 0.002 м, a4 = -0.007 м, g1 = 40p рад/с, gN = 3.6p рад/с,
F1 = 1.2 н, FN = 11.5 н, a1=F1/m1= 0.6 м/с2, aN = FN/mN = 5.75 м/с2, w= 3.3166 рад/с,
w1 = 5.244
рад/с, l1= 5.244
рад/с, l2 =
6.2048 рад/с, z1=zN= 2.75(рад/с)2. Перемещения представлены на графиках рисунка 2
по формулам (5), (6) и таблицы 1

![]() (7)
(7)

 (8)
(8)
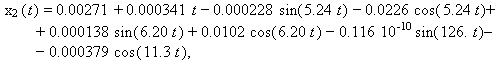
 (9)
(9)
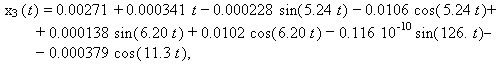
 (10)
(10)
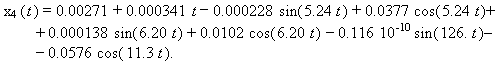
 (11)
(11)
 а)
а)
 б)
б)
 в)
в)
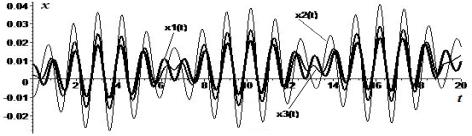
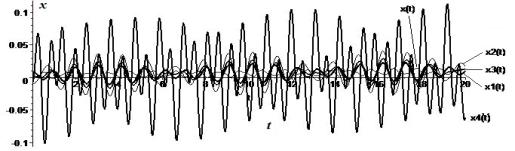
Рисунок 2 -
Аналитические графики перемещений xj(t), j = ![]() на а и б; численный расчет
общей динамической задачи с разными начальными условиями aj на б
на а и б; численный расчет
общей динамической задачи с разными начальными условиями aj на б
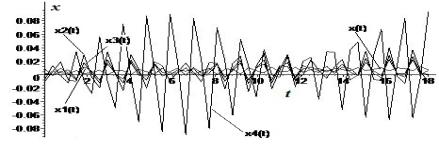
Численная реализация задачи (1)-(3) на рисунке 2 в наглядно демонстрирует приблизительный
характер вычислений, достаточно грубое округление величин, при этом счет обрывается
на параметре времени t=18 c. Точный
расчет является убедительно доказательным, позволяющим получить явные законы
колебаний осцилляторов, подвешенных на одной балке. Подтверждением истинности
представленных результатов (7)-(11) могут служить начальные условия. На рисунке
2 а, б наблюдается небольшое рассогласование по фазам колебаний
гармонических осцилляторов и заметное отличие по амплитудам. В этом случае движения
элементов с массами m1,
m2, m3 являются «почти синхронными». Общий
вид графиков, линейно смещающихся вниз вместе с подвесом массой М в соответствии с выбранной системой
координат на рисунке 1, пропорционален параметру времени t и вполне согласуется с поставленной задачей о
колебаниях многоэлементной динамической системы на одной неупругой балке с жесткой
заделкой. Более синхронизированной данная система станет, если в формулах
таблицы 1 положить все начальные условия aj, j
= ![]() одинаковыми. Например, aj=0.005м, j=
одинаковыми. Например, aj=0.005м, j=![]() , n=4, M=20.0
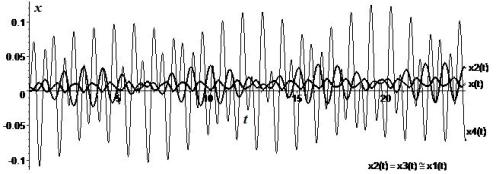
кг, m1=m2=m3=m4= 2.0 кг, c1=c2=c3=c4= 55.0 н/м, g1= 40p рад/с, gN=3.6pрад/с, F1= 1.2 н, FN = 11.5 н, a1=F1/m1= 0.6 м/с2, aN =FN/mN = 5.75 м/с2, w=3.3166 рад/с, w1= 5.244 рад/с, l1= 5.244 рад/с, l2= 6.2048 рад/с, z1=zN=2.75(рад/с)2. Перемещения x(t), x1(t), x2(t), x3(t), x4(t) отображены в виде графиков на рисунке
3
, n=4, M=20.0
кг, m1=m2=m3=m4= 2.0 кг, c1=c2=c3=c4= 55.0 н/м, g1= 40p рад/с, gN=3.6pрад/с, F1= 1.2 н, FN = 11.5 н, a1=F1/m1= 0.6 м/с2, aN =FN/mN = 5.75 м/с2, w=3.3166 рад/с, w1= 5.244 рад/с, l1= 5.244 рад/с, l2= 6.2048 рад/с, z1=zN=2.75(рад/с)2. Перемещения x(t), x1(t), x2(t), x3(t), x4(t) отображены в виде графиков на рисунке
3
 а)
а)
 б)
б)
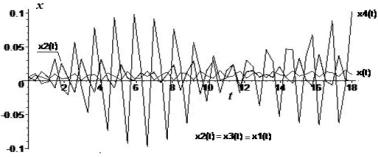
Рисунок 3 -
Аналитические графики перемещений xj(t), j = ![]() на а; численный расчет общей динамической задачи с одинаковыми начальными aj условиями на б
на а; численный расчет общей динамической задачи с одинаковыми начальными aj условиями на б
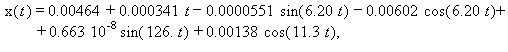
(12)
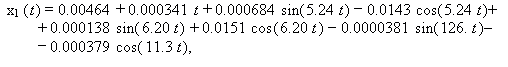
(13)

(14)

(15)
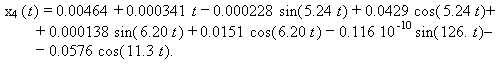
(16)
Аналитические формулы перемещений (14) и (15) достоверно
показывают, что синхронными будут колебания внутренних элементов механической
системы с одинаковыми отклонениями масс m j в начальный момент времени aj = a0, j = ![]() , поскольку два колебательных
режима x2(t) и x3(t) полностью совпали. Это очевидно
проиллюстрировано на рисунке 3 а, б.
, поскольку два колебательных
режима x2(t) и x3(t) полностью совпали. Это очевидно
проиллюстрировано на рисунке 3 а, б.
Выводы. На основе развитой авторами методики
[3-5] решения динамических задач многоэлементных механических систем со специальными
нагрузочными режимами получены аналитические формулы колебаний произвольного числа n линейных осцилляторов на общей
жесткой связи. Учет влияния последней приводит к появлению слагаемых вида А12t и ![]() в решениях (5), (6) поставленной
задачи (1)-(3), что является отрицательным
фактором и противоречит физической сути рассматриваемого явления, несмотря на малость
коэффициентов. Тем не менее, синхронными будут
колебания внутренних n-2 элементов из
n автономных
осцилляторов с одинаковыми отклонениями масс mj (j =
в решениях (5), (6) поставленной
задачи (1)-(3), что является отрицательным
фактором и противоречит физической сути рассматриваемого явления, несмотря на малость
коэффициентов. Тем не менее, синхронными будут
колебания внутренних n-2 элементов из
n автономных
осцилляторов с одинаковыми отклонениями масс mj (j = ![]() ) в начальный момент времени.
) в начальный момент времени.
Литература
1. Блехман И.И. Синхронизация
в природе и технике.- М.: Наука, 1981. -352
с.
2. Пиковский A.C., Розенблюм
М.Г., Курте Ю.
Синхронизация: Фундаментальное нелинейное явление.- М.: Техносфера, 2003. - 494 с.
3. Dokukova N. A. and
Konon P. N. General laws governing in mechanical vibratory systems// JEPT,
2006, V. 79, N. 4, P. 824-831, Pub. Springer New York, ISSN: 1062-0125.
4. Dokukova N.
A., Martynenko M. D. and Kaftaikina E. N. Nonlinear vibrations of hydraulic
shock absorbers// JEPT, 2008, V. 81, N. 6, P.
1197-1200, Springer NY.
5. Dokukova N.A., Kaftaikina E.N.: The synchronization of two linear
oscillators// Materialy VII miedzynarodowej naukowi-praktycznej konferencji.
Przemysl, Polska. 7-15 listopada 2012 r. Przemysl: Nauka i studia, V. 18, P. 28 – 35.