Физика. Физика полимеров

Баруздина О.С., Байджанов А.Р., Моисеева А.И.

Череповецкий государственный университет

Процесс оптимизации технологического процесса производства полимерных покрытий

Проблема оптимизации управления процессами нанесения и сушки полимерного покрытия на поверхности металла сформулирована в форме задачи Майера - Больца. Для ее решения введен ряд целевых базисных функционалов , где r – заданные, u – управляющие функции. Индекс i принимает два значения: при i = 1 целевой функционал относится к сушильной печи грунтовочного слоя, при i = 2 – к отделочной печи. К заданным параметрам функционала r можно отнести тип грунтовки или лакокрасочного материала, параметры печи, размеры металлического листа. Управляющими функциями u(x) являются температурные режимы грунтовочной и отделочной сушильных печей, а также скорость движения металлического листа в печи.

Для прогнозирования качества покрытия введем обобщенный функционал, который является произведением нескольких базисных. Рассмотрим несколько целевых функционалов:

, (1)

где μ – параметр ориентационного порядка в полимерном слое;

, (2)

где θ – коэффициент прилипания грунтовки к металлу (i=1) и лакокрасочного материала к грунтовочному слою (i =2);

(3)

где – доля мономеров, вступивших в реакцию полимеризации - общее число мономеров);

, (4)

где t (x) - температура внутри сушильной печи, - температура окружающего воздуха, х – координата точки движущейся полосы внутри печи, длиной L .

Также введены обобщенные функционалы:

, (5)

Вследствие того, что для получения качественного покрытия функционалы имеют области значений [0, 1], обобщенные функционалы являются ограниченными сверху, поэтому при определенном значении управляющих параметров они должны принимать максимальные значения.

Так как функционалы определяются с помощью метода Монте-Карло, то аналитическое решение поставленной вариационной задачи не представляется возможным. Кроме того, решение этой задачи обычными методами теории оптимального управления также затруднено, так как значения функционалов имеют разброс, вследствие использования случайных чисел в методе Монте-Карло.

Допустим, задача решена и найден оптимальный технологический режим, т.е. искомая зависимость t_i^*(x) температуры от координаты текущей точки листа. Результаты технологических испытаний, проведенной фирмой “GATV GmbH”, показывают, что оптимальный температурный режим для покрытия является нелинейной возрастающей функцией [1]. Здесь функция t^*(x) была аппроксимирована степенной функцией (6):

₍₆₎

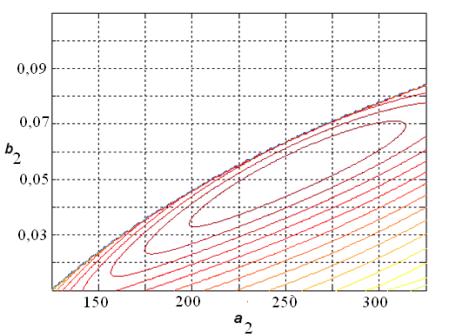
Поэтому нахождение оптимального температурного режима сводится к определению параметров а_i и b_i, а рассматриваемая вариационная задача сводится к проблеме нахождения максимума функции двух переменных F^*_i (a_i,b_i). На рис.1. приведены линии уровня функций F^*₂(a₂,b₂) для поливинилиденфторидова (ПВДФ) покрытия при скорости движения полосы 1 м/с. Видно, что функция F^*₂(a₂,b₂) имеют достаточно пологий максимум, то есть данная задача имеет устойчивое решение.

Рис.1. Линии уровня функции F^*₂(a₂,b₂) ПВДФ покрытия.

Заключение

Показано, что в зависимости от химического строения покрытия существует оптимальный температурный режим печи для сушки полимерного покрытия, который можно определить, используя разработанные алгоритмы и программное обеспечение

Литература:

1. Matamoros, S. Подробное описание печной установки для печи грунтовочного слоя и печи отделочного слоя и термореактора АПП / S. Matamoros. - Леверкузен: gatv mbH, 2005.