Строительство и Архитектура /
Строительство
Автор:
профессор Бубнович Э.В., магистрант Абилденова Г.
Казахский
Национальный Технический Университет имени К.И.Сатпаева г .Алматы Казахстан
Исследование резонансов при вынужденных
взаимосвязанных колебаниях гибкой нити
В
настоящей статье основное внимание уделяется изучению колебаний нити при
одновременном возникновении внешнего и внутреннего резонанса первого и второго
порядка. Выводятся амплитудно-частотные зависимости для стационарных режимов
колебаний.
В
нелинейной механической системе с несколькими степенями свободы, в зависимости
от соотношений между собственным частотами и частотой внешнего возмущения,
можно возбудить параметрические резонансные, вынужденные резонансные и
комбинационные резонансные колебания Параметрический резонанс изучался в связи
с задачами динамической устойчивости
конструкций [1, 2, 3, 4, 5], резонанс второго типа подробно изучен в
[6], а комбинационный резонанс рассмотрен в [7].
Рассматриваются
вынужденные колебания гибкой пологой нити с неподвижными опорами на одном
уровне. Считается, что нить одновременно может совершать поперечные колебания в
своей плоскости и маятниковые колебания относительно хорды, соединяющей опорные
закрепления.
1.
Поперечные перемещения нити будем аппроксимировать следующим выражением
![]()
![]()
![]() (1.1)
(1.1)
В этой сумме первое слагаемое - отклонение нити от
действия статической нагрузки; второе - поперечное динамическое перемещение
нити.
Подставляя выражения для кинетической и
потенциальной энергии системы в уравнение. Лагранжа второго рода и учитывая (1.1), а также условие статического равновесия
нити, приходим к системе двух нелинейных дифференциальных уравнений:
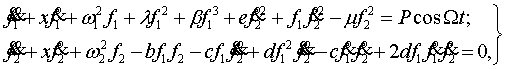 (1.2)
(1.2)
где ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (1.3)
(1.3)
![]()
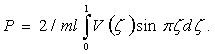
Здесь ![]()
![]() - обобщенные координаты
поперечных и маятниковых колебаний;
- обобщенные координаты
поперечных и маятниковых колебаний; ![]() - погонная масса нити;
�� - пролет;
- погонная масса нити;
�� - пролет; ![]() - стрела начального
провисания;
- стрела начального
провисания; ![]() - величина предварительного напряжения;
- величина предварительного напряжения; ![]() - модуль упругости материала;
- модуль упругости материала; ![]() - площадь поперечного сечения нити;
- площадь поперечного сечения нити; ![]() - ускорение силы тяжести; h - коэффициент вязкого
трения; V(x) -
интенсивность внешнего воздействия;
- ускорение силы тяжести; h - коэффициент вязкого
трения; V(x) -
интенсивность внешнего воздействия; ![]() - отношение
парциальных частот линейных маятниковых и поперечных колебаний нити;
- отношение
парциальных частот линейных маятниковых и поперечных колебаний нити; ![]() - частота
возмущающего воздействия.
- частота
возмущающего воздействия.
Для исследования поставленной задачи
применим метод, аналогичный методу Страбла [8], который является комбинацией
двух классических методов, а именно: вариации произвольных постоянных и
разложения в ряд по методу возмущений.
В качестве возможной формы решения
системы (1.2) выбираем следующие ряды:
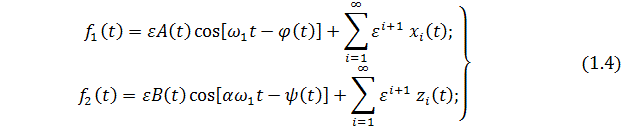
где ![]() - малый параметр;
- малый параметр; ![]() - вариационные параметры;
- вариационные параметры; ![]() - аддитивные поправки, называемые
короткопериодическими возмущениями.
- аддитивные поправки, называемые
короткопериодическими возмущениями.
За малый параметр ![]() , после приведения
системы (1.2) к безразмерному виду, принята величина 2
, после приведения
системы (1.2) к безразмерному виду, принята величина 2![]() /
/![]() .
.
Исследуем сначала случай, когда условия
внутреннего и внешнего резонанса не выполняются, т.е. значение �� существенно отличается
от ½ и 1, а частота возмущающей силы далека от собственной частоты
поперечных колебаний нити. В этом случае решение системы дифференциальных
уравнений, полученных в результате подстановки (1.4) в (1.2), с точностью до
малых первого порядка сводится к частным интегралам
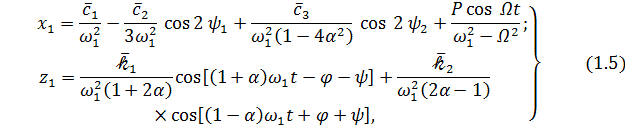
где ![]()
![]()
![]()
![]()
![]()
![]()
![]()
При выводе (1.5) предполагалось, что
вариационные параметры в разложении (1.4) являются постоянными.
2. Предположим, что условия внешнего
резонанса и внутреннего резонанса первого порядка (главного внутреннего
резонанса системы) выполнены, т.е. Ω/![]() ��→1/2. Будем считать, что
вариационные параметры являются некоторыми функциями времени, а их производные
- малые величины порядка ε. Теперь некоторые члены в (1.5) либо обращаются
в бесконечность, либо становятся весьма большими. Чтобы этого избежать,
перенесем резонансные члены в вариационную часть системы дифференциальных
уравнений. Тогда, в результате некоторых преобразований и замены вариационных
уравнений приведенной системой с точностью до ε получим
��→1/2. Будем считать, что
вариационные параметры являются некоторыми функциями времени, а их производные
- малые величины порядка ε. Теперь некоторые члены в (1.5) либо обращаются
в бесконечность, либо становятся весьма большими. Чтобы этого избежать,
перенесем резонансные члены в вариационную часть системы дифференциальных
уравнений. Тогда, в результате некоторых преобразований и замены вариационных
уравнений приведенной системой с точностью до ε получим
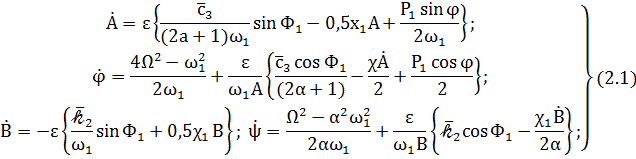
где ![]() =(2��-1)
=(2��-1)![]()
Введение
малого параметра в возмущение (P=��![]() ) дает возможность подробно
изучить структуру решения в области внешнего резонанса.
) дает возможность подробно
изучить структуру решения в области внешнего резонанса.
В дальнейшем будем рассматривать
стационарный режим вынужденных колебаний. Приравнивая нулю правые части
уравнений (2.1) и решая полученную систему, найдем амплитудно-частотные
зависимости для поперечных и маятниковых колебаний нити
![]()
![]() .
.
где ![]() =b+c
=b+c![]()
![]()
Частные решения уравнений относительно
короткопериодических возмущений запишутся в форме
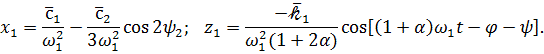
Для составления условий устойчивости стационарных режимов
вынужденных колебаний нити образуем уравнения в вариациях. Для этого в
приведенной системе вариационных уравнений (2.1) сделаем подстановку:
![]()
В
результате получим систему четырех дифференциальных уравнений. Принимая решение
этой системы в виде: ![]() где
где ![]() и раскрывая характеристический
определитель, будем иметь:
и раскрывая характеристический
определитель, будем иметь:
![]() где
где ![]() коэффициенты, зависящие от параметров системы
и амплитуд A и В.
коэффициенты, зависящие от параметров системы
и амплитуд A и В.
Согласно критерию Рауса – Гурвица,
колебания нити устойчивы при выполнении следующих неравенств:
![]() (2.2)
(2.2)
Неравенства
(2.2) позволяют определить устойчивые и неустойчивые ветви амплитудно-частотных
характеристик.
3. Если уточнять решение уравнений
колебаний нити для значений α, отличающихся от 1/2, то в этом случае
обнаруживаются явления внутреннего резонанса и при α, близком к
единице. Исследуем поведение нити в
условиях внешнего резонанса и внутреннего резонанса второго порядка, т.е. ![]()
Подставляя (1.5) в (1.2) и удерживая
члены порядка ![]() , в результате некоторых
преобразований найдем
, в результате некоторых
преобразований найдем
![]()
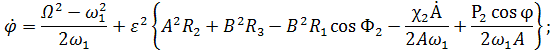
![]()
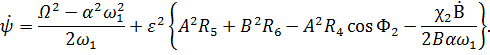
Здесь ![]()
![]()
![]()
![]() – коэффициенты, зависящие
от параметров нити.
– коэффициенты, зависящие
от параметров нити.
Для определения амплитуд поперечных и
маятниковых колебаний нити в установившемся режиме получим следующую систему
алгебраических уравнений:
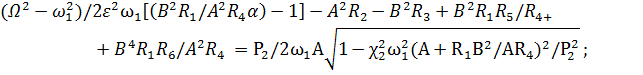
![]()
![]() (3.1)
(3.1)
Если в (3.1) положить ![]() , то будем имтеь
, то будем имтеь
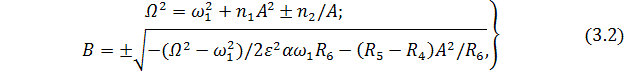
где ![]() - коэффициенты, зависящие от параметров
системы и внешнего воздействия.
- коэффициенты, зависящие от параметров
системы и внешнего воздействия.
Резонансное
решение во втором приближении имеет частные интегралы
![]()
![]() 251658240
251658240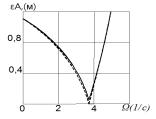 251658240
251658240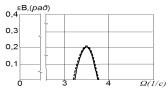
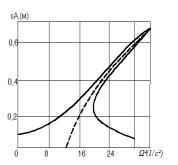
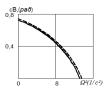
рис. 1 рис. 2 рис. 3 рис. 4
![]()
![]()
Пример.
Рассмотрим нить со следующими параметрами: ![]() , E=157∙
, E=157∙![]() Н/
Н/![]() ; F=12∙
; F=12∙![]() ;
; ![]()
![]()
![]() Вычисляя коэффициенты по формулам (1.3),
найдем:
Вычисляя коэффициенты по формулам (1.3),
найдем: ![]() (рад/
(рад/![]() ;
; ![]() (рад/
(рад/![]() ;
; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Результаты численного
анализа представлены на рис. 1-4. Из графика амплитудно-частотной зависимости
(рис. 1) видно, что при частоте возмущения, равной частоте маятниковых
колебаний, амплитуда поперечных колебаний нити минимальна, в то время как
амплитуда маятниковых колебаний достигает максимальных значений (рис. 2). С
увеличением Р эти значения возрастают.
Для случая резонансных колебаний нити
второго порядка амплитудно-частотные
характеристики показаны на рис. 3 и 4 (пунктиром на рис. 1, 2 и 4
показаны амплитудно-частотные зависимости без учета демпфирования).
Из формулы (3.2) и рис. 3 видно, что
резонансная кривая для амплитуды поперечных колебаний нити с точностью до
постоянных совпадает с амплитудно-частотными зависимостями систем типа
Дуффинга.
Таким образом, решения, полученные в
первом и втором приближениях, создают
достаточно ясное представление о стационарных колебаниях нити в условиях
одновременного возникновение внешнего и внутренних резонансов. Наиболее опасным
является влияние внешнего воздействия на нить при наличии главного внутреннего
резонанса. В этом случае при частоте возмущающей силы, большей частоты
маятниковых линейных колебаний нити, амплитуда поперечных колебаний начинает
резко возрастать. При проектировании вантовых систем необходимо обратить особое
внимание на возможность возникновения таких явлений.
СПИСОК
ЛИТЕРАТУРЫ
1.
В.
А. Ивович Взаимосвязь при колебаниях виброизолированных систем. «Строительная механика и расчет сооружений»
, 1971, № 2.
2.
Э.В.
Бубнович Автопараметрические колебания гибкой пологой нити. Реферативный
сборник “Сейсмостойные строительство”, М., 1975
3.
Н.
А. Николаенко, А. Т. Штоль Динамическая устойчивость и статистический анализ
колебаний нелинейной параметрической системы. «Строительная механика и расчет
сооружений», 1970, № 1.
4.
В.
В. Болотин Динамическая устойчивость упругих систем. ГИТТЛ, 1956.
5. R. W. Evan-Jwanowski “On the
Parametric Response of Structures”, Applied Mechanics Review, vol. 18, NO. 9,
Sept., 1965.
6.
Н.
Н. Боголюбов, Ю. А. Митропольский Асимптотические методы в теории нелинейных
колебаний. М., Физматгиз, 1965.
7. E. Mettler Combination Resonance in Mechanical Systems under Harmonic
Excitations, 4th Conference on Nonlinear Oscillations, Prague, 1967.
8. R. A. Struble Nonlinear
Differential Equations, McGraw Hill, New York, 1 962.