Yuriy Zachinyaev, Konstantin Rumyancev

Southern Federal University, Russia

Fiber-optic Based Generator of Nanosecond Linear

Frequency Modulated Signals

Several techniques to generate the LFM (chirp) signal have been proposed over the past few decades. Generally all the techniques can be categorized into 3 types: analog generator approach, dispersive delay line approach (surface acoustic wave (SAW) generators) and digital approach [1, 2].

Analog approach involves analog radio technical methods of producing LFM chirps using controlled LC-generators, phase modulators, dispersive SAW time delay lines. Generating high-frequency chirps (1-20 GHz) involves such devices as backward-wave tubes, reflex klystrons and yttrium iron garnet (YIG) generators.

Unlike analog chirp generator the properties of the digitally generated waveform (type of modulation, start and stop frequency, waveform output duration) can be configured easily by changing the firmware and memory contents of the digital generator. Two of the most popular digital chirp generator architectures are the Memory-based architecture and Direct Digital Synthesizer (DDS) architecture. At the same time, digital method has some serious disadvantages: the necessity of using additional devices for frequency mixing and inability to produce large time-bandwidth signals.

The minimal chirp pulse width is provided by SAW devices and backward-wave tubes based generator while the chirp rate is maximum in backward-wave tubes based generators. Such values make LFM signals hardly usable in such applications as radio tomography, underground location and high speed secure communications since having large dead zone.

Impossibility of using traditional methods for high-speed generating and processing of UWB signals including the LFM signals makes it necessary to use optical methods of data processing including the application of fiber-optic structures for this purpose. The appropriateness of such structures application is due to the properties of optical fibers: dramatically low light signals power loss (less than 0.2 dB/km), broad bandwidth per unit length (over 500 GHz·km), excellent electromagnetic compatibility with any electrical and radio equipment and perfect galvanic isolation from him, high noise immunity, small dimensions, weight and topological flexibility [4].

The applications of optical fibers in the purposes of radio signals generating and processing were revealed when the latter came to be regarded as a key element of optical signal delay lines. It was shown that the potential of optical fiber as an optical delay line for light signals modulated with the radio frequency are out of competition compared with well-known in radio physics devices in such critical parameters as normalized modulated light signal loss and time-bandwidth product. According to these facts, a new method of the LFM signals generating is suggested. Architecture for this method is shown on the Fig. 1.

Figure 1. Architecture of the optical LFM generator [4,7]

Picosecond pulse optical generator produces a short pulse of certain amplitude and submits it to the fiber-optic array that consists of optical splitter, optical coupler and the number of binary optical structures and optical delay lines (Fig.2.а).

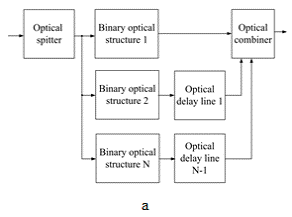
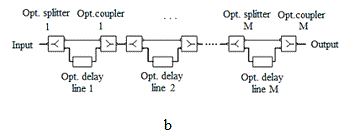
Figure 2. Architecture of Fiber-optic array (a) and architecture of the Binary fiber-optic structure (b) [4, 5, 7]

Every binary optical structure in array produces K copies of the input signal with pulse width and repetition period :

. (1)

Binary fiber-optic structures from all other optical structures ensure a high level of identity of copies and a low consumption of fiber (Fig. 2.b).

Thus the fiber-optic array produces N⋅K copies of the input picosecond impulse, where N - number of Binary optical structures in array. Structures in array differ by the repetition period of the copies that can be calculated for the n-th structure with [5]

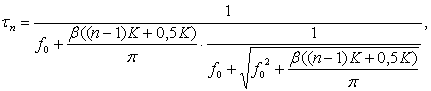(2)

where is initial frequency of LFM signal, - chirp rate. Number of copies generated by each structure can be found with

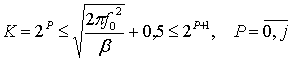. (3)

Finally the number of structures in array N is calculated with

, (4)

where - the duration of the LFM signal, - central frequency of LFM signal.

From the output of the Binary optical structures array a sequence of optical pulses is fed to the photo receiver module that converts the optical signal into electrical. Finally, the first harmonic of the resulted signal is allocated using a band pass filter. After additional filtering and amplification, signal is radiated by antenna. The results of computer modeling for the LFM signal with = 9,25 ns, = 1081 GHz/µs are shown on the Fig. 3 ((a) – spectral density, (b) – signal on the correlator output).

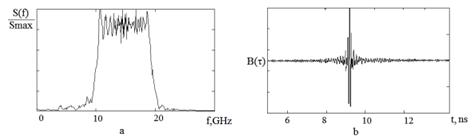
Figure 3. Results of optical chirp generation modeling

The suggested method allows producing LFM signals with duration from 2 ns and chirp rate up to 3000 GHz/µs [5]. For evaluation of the conditions of the functioning of the fiber-optic based chirp generator a simulation was performed using MATLAB software. The minimum of autocorrelation function side lobe peak level has been chosen as criteria for evaluation of the chirp signal quality. Simulation was held with the following parameters: chirp duration = 2.2 ns, the central frequency of the chirp signal = 10.1 GHz; frequency deviation =5.89 GHz; the required power output = 100 mW; average output optical power of optical generator = 10 mW; the signal / noise ratio at the output of the generator SNR = 50 dB.

Measured pulse width is 2.1 ns (minus 3 dB level) which is 4.5 % different from the value provided by the design. Output power = 103 mW, which is 2.9 % different from the value provided by the design.

Analysis of the dependence of the ambient temperature fluctuations on the parameters of the fiber-optic based chirp generator with zero optical fiber length manufacturing intolerance was performed using the following parameters: optical fiber length manufacturing intolerance =0, the ambient temperature fluctuation range from -60 to 60 ° C with steps of 5 ° C The results of simulation in graphic form for the generator without amplitude weighting (a) and with amplitude weighting (b) are shown on Fig. 4.

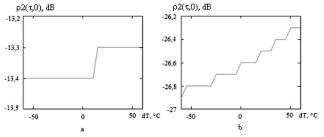
Figure 4. The value of autocorrelation sidelobe peaks depending on the ambient temperature fluctuations

As shown on Fig.4 for the chirp signal with pulse width of 2.2 ns according to above specified conditions temperature fluctuations have little effect on the correlation properties of chirp. For generator without amplitude weighting slight increase in sidelobe peaks values (0.1 dB) occurs in cases when the ambient temperature raises by more than 15 ° C (above 42 ° C) that if necessary requires additional cooling. In case of reducing the ambient temperature level the autocorrelation sidelobe peak values remain unchanged. For generator with amplitude weighting slight increase in sidelobes (0.1 dB) occurs in cases when the ambient temperature raises by more than 20 ° C (above 47 ° C), and 0.3 dB when the ambient temperature raises by more than 23 ° C. At the same time reducing the ambient temperature leads to reduction of the level of sidelobe peak values by 0.3 dB (at = 60 ° C).

Analysis of the influence of the optical fiber length manufacturing intolerance on the parameters of the fiber-optic based chirp generator with zero ambient temperature fluctuations was performed using the following parameters: ambient temperature fluctuation value = 0° C; manufacturing error range is in -1 to 1 mm diapason with a variable pitch.

The results of simulation in graphic form for the generator without amplitude weighting (a) and with amplitude weighting (b) are shown on Fig.5.

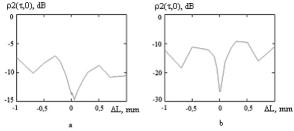
Figure 5. The value of autocorrelation sidelobe peaks depending on the optical fiber length manufacturing intolerance

As can be seen from Fig.5 the increase of manufacturing inaccuracies leads to the increase of the sidelobe peak values. For different cases of amplitude weighting application the shape of curves is similar with the difference in the value of the sidelobes.

The work was performed as part of the state task of the Ministry of Education and Science of the Russian higher education institutions in terms of scientific research. Project № 213.01-11 / 2014-9.

References:

1. Kochemasov V. N., Belov L. A., Okoneshnikov V. S. Formirovanie signalov s linejnoj chastotnoj moduljaciej. M.: Radio i svjaz', 1983. 192 p.

2. Merrill I. Skolnik. Radar Handbook (2nd Edition). - McGraw-Hill, 1990. 1220 p.

3. Zachinyaev Y. V. Analiz i klassifikacija formirovatelej linejno-chastotno-modulirovannyh radiosignalov c tochki zrenija umen'shenija dlitel'nosti formiruemyh signalov // Sovremennye problemy nauki i obrazovanija. 2012. № 5. URL: http://www.science-education.ru/105-7173 (date of submission: 12.10.2013)

4. Zachinyaev Y. V., Rumyantsev K.E. Assessment of the influence of physical factors on the operational features of the linear frequency shift keying signal generator based on the fiber optic structures // Izvestija vysshih uchebnyh zavedenij Rossii. Radiojelektronika, 2012. № 4. p. 91-101

5. Kukujashnyj A.V. Osobennosti formirovanija LChM signalov s ispol'zovaniem volokonno-opticheskih struktur // Informacionnoe protivodejstvie terrorizmu. 2007. №9. p. 75-88.

6. Rumyantsev K.E., Gorbunov A.V. Dinamicheskie zapominajushhie ustrojstva na osnove binarnyh volokonno-opticheskih struktur // Radiotehnika. 2002. №12. p. 73-80

7. Zachinyaev Y. V., Rumyantsev K.E., Kukujashnyj A.V. Formirovanie nanosekundnyh LChM-radiosignalov na volokonno-opticheskih strukturah // Jelektrotehnicheskie i informacionnye sistemy i kompleksy. 2011. P.7, №3. p. 32-38.