Талайбеккызы Наргиза.

Моделирование сценария рождения аттрактора Ресслера и его бифуркации.

Ресслером был предложен ряд нелинейных систем обыкновен­ных дифференциальных уравнений для моделирования некоторых ги­потетических химических реакций, обладающих хаотическим поведе­нием. Система состоит из трех ОДУ и имеет три параметра модели. Поскольку неизвестных функций три, то фазовый портрет системы должен определяться не на плоскости, а в трехмерном пространстве.

Модель Ресслера:

Решением системы Ресслера при определенном сочетании параметров является странный аттрактор (или аттрактор Ресслера) – притягивающее множество траекторий на фазовом пространстве, которое по виду идентично случайному процессу. В некотором смысле аттрактор Ресслера является стохастическими автоколебаниями, которые поддерживаются в динамической системе за счет внешнего источника.

Решение в виде странного аттрактора появляется только при некоторых сочетаниях параметров. Критическое сочетание параметров, при которых фазовый портрет системы качественно меняется, называется в теории динамических систем точкой бифуркации. Физический смысл бифуркации в модели Ресслера, согласно современным представлениям, описывает переход ламинарного движения жидкости к турбулентному.

Система дифференциальных уравнений, решение которой, приводит к созданию аттрактора Ресслера имеет вид:

.    (1)

Поведение решения системы при изменении одного из коэффициентов.

При a := 0.5; b := 0.75;   (рис.1)

Рис.1

Трехмерное изображение

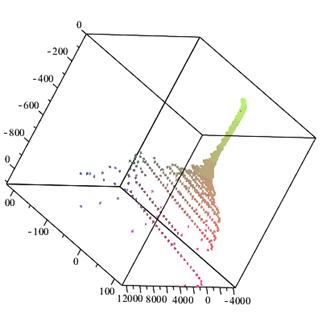
Изображение по оси OX,OY,OZ.

 

 

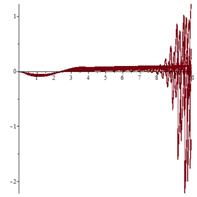
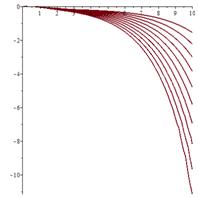
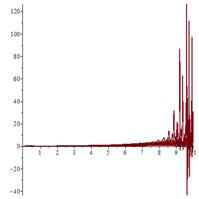
Исследование сценария перехода к хаосу в данной системе проведем при фиксированных значениях параметров и .

•           (рис.2)

 

Рис.2

Трехмерное изображение

 

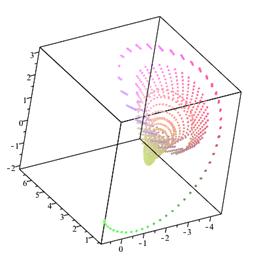
Изображение по оси OX, OY,OZ/

 

 

 

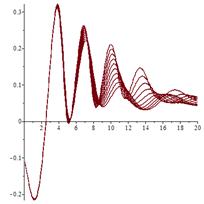
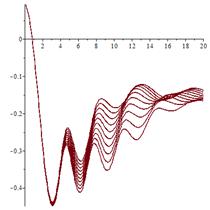
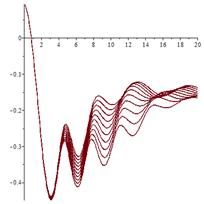
С ростом значений параметра  в системе (1) наблюдается каскад бифуркаций удвоения периода исходного цикла.

Список используемых источников

1. Н. А. Магницкий, С. В.Сидоров НОВЫЕ МЕТОДЫ ХАОТИЧЕСКОЙ ДИНАМИКИ.

2. Итоги науки техники. Современные проблемы математики. Фун­даментальные направления. Динамические системы.-М.: ВИНИТИ, 1985, т. 1, 243 с., т. 2, 312 с.