Чиркова
Л.Н., к.п.н.
Вятский
Государственный Университет, Россия
Понятие
верхнего и нижнего пределов функций
Определим понятия верхнего и нижнего
пределов функции f(x).
Пусть точка x0 –
предельная точка области определения ![]() функции f(x).
функции f(x).
Определение. Число а
– верхний предел функции
f(x)
при
![]() (обозначается символом
(обозначается символом
![]() ), если выполняются следующие условия:
), если выполняются следующие условия:
1) ![]()
![]() :
: ![]() и
и ![]()
![]()
![]() ;
;
2) ![]()
![]() ,
, ![]() ,
, ![]() :
: ![]() .
.
Если в любой проколотой окрестности точки x0 функция принимает как
угодно большие положительные (отрицательные) значения, то по определению
полагаем: ![]() (
(![]() ).
).
Определение. Число а
– нижний предел функции f(x) при ![]() (обозначается как
(обозначается как ![]() ), если выполняются следующие условия:
), если выполняются следующие условия:
1) ![]()
![]() :
: ![]() и
и ![]()
![]()
![]() ;
;
2) ![]()
![]() ,
, ![]() ,
, ![]() :
: ![]() .
.
Если в любой проколотой окрестности точки x0 функция принимает как
угодно большие отрицательные (положительные) значения, то по определению
полагаем ![]() (
(![]() ).
).
Рассмотрим множество
значений {f(x)} функции f(x) на ![]() . Рассмотрим
. Рассмотрим ![]() . При уменьшении
. При уменьшении ![]() эта величина является невозрастающей
функцией от
эта величина является невозрастающей
функцией от ![]() (ограниченной или неограниченной снизу), и, следовательно, существует
(ограниченной или неограниченной снизу), и, следовательно, существует
![]() (конечный, если
функция ограничена снизу, или бесконечный в противном случае). Тогда сформулируем
определение верхнего предела в терминах точной верхней грани: предел
(конечный, если
функция ограничена снизу, или бесконечный в противном случае). Тогда сформулируем
определение верхнего предела в терминах точной верхней грани: предел ![]() называют верхним пределом функции f(x) при
называют верхним пределом функции f(x) при ![]() , т.е.
, т.е. ![]() . Аналогично, предел
. Аналогично, предел ![]() называют нижним пределом функции f(x) при
называют нижним пределом функции f(x) при ![]() .
.
Известно, что ![]() не существует. Найдем
верхний и нижний пределы функции
не существует. Найдем
верхний и нижний пределы функции ![]() при
при ![]() :
:
![]() ;
; ![]() .
.
Для функции ![]() верхний и нижний
пределы при
верхний и нижний
пределы при ![]() есть:
есть:
![]() ;
; 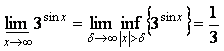 .
.
Функция ![]() имеет верхний и нижний
пределы при
имеет верхний и нижний
пределы при ![]() , при этом они равны:
, при этом они равны:
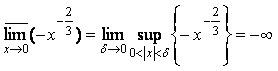 ;
; 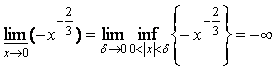 .
.
Введем определения
верхнего и нижнего пределов функции при ![]() , используя понятие частичного предела функции в точке x0: если
, используя понятие частичного предела функции в точке x0: если ![]() ,
, ![]() ,
, ![]()
![]()
![]() , то у называется частичным пределом функции в точке
, то у называется частичным пределом функции в точке ![]() .
.
Определение.
Наибольший из всех частичных пределов функции f(х) при ![]() назовем верхним пределом функции f(х), наименьший из всех частичных
пределов функции f(х) при
назовем верхним пределом функции f(х), наименьший из всех частичных
пределов функции f(х) при ![]() называется нижним пределом функции f(х).
называется нижним пределом функции f(х).
Например, 0 – частичный
предел функции ![]() в точке x0=0, так как при
в точке x0=0, так как при ![]() последовательность
последовательность ![]() . Но при
. Но при 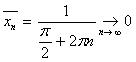 последовательность
последовательность ![]() при
при ![]() стремится к 1, и
стремится к 1, и ![]() для всех
для всех ![]() , то верхний предел
, то верхний предел ![]() равен 1.
равен 1.
![]() , поскольку наименьший из всех частичных пределов получается
при
, поскольку наименьший из всех частичных пределов получается
при 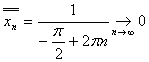 , так как
, так как ![]() , и
, и ![]() для всех
для всех ![]() .
.
Существуют и другие
определения понятий верхнего и нижнего пределов функции в данной точке [1, с.33-35].
В цитируемом источнике показано, что все определения верхнего (нижнего) предела
эквивалентны между собой.
Введем понятия верхней
и нижней бесконечно малых функций в точке x0:
функция ![]() называется верхней бесконечно малой в точке x0, если
называется верхней бесконечно малой в точке x0, если ![]() , и нижней бесконечно
малой в точке x0, если
, и нижней бесконечно
малой в точке x0, если
![]() .
.
Например,
функция ![]() является верхней
бесконечно малой при
является верхней
бесконечно малой при ![]() , так как
, так как ![]() , функция
, функция 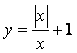 является нижней
бесконечно малой при
является нижней
бесконечно малой при ![]() , так как
, так как 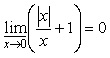 .
.
Литература:
1.
Брайчев Г. Г. Введение в теорию роста
выпуклых и целых функций. М.: Прометей, 2005. 232 с.