МАТЕМАТИКА/5.Математическое моделирование

к.ф.-м.н. Искакова А. С., Токсанова С.С.

Евразийский национальный книверситет имени Л.Н. Гумилева, Астана, Казахстан

Об построении эмпирической зависимости cоциальных выплат страхового портфеля на случай потери работы

Модели прогнозирования, как отражение существующей реальности, оказываются совершенно необходимыми для описания очень многих явлений и ситуаций, встречающихся в повседневной жизни.

Одной из характерных особенностей поставленных перед управлением страховыми компаниями Республики Казахстан является составление прогнозов социальных выплат страхового портфеля.

Рассмотрим построение эмпирической функции«страховой компании» на случай потери работы, заданной графически.

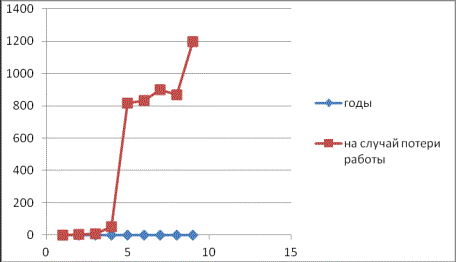
По консолидированной финансовой отчетности АО «Государственный фонд социального страхования» имеем статистические данные за последние 9 лет.

Нас интересует, как выглядит функциональная зависимость между x_i и y_i, где i принимает любые натуральные конечные значения.

Пусть y – функция одной переменной с двумя параметрами a и b. В качестве набора выбора функций, из которых будем иметь эмпирическую зависимость, рассмотрим:

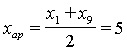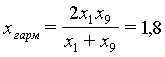Для наилучшего выбора вида аналитической зависимости y=f(x,a,b) построим следующие промежуточные вычисления. На заданном отрезке изменения независимой переменной выбирают точки, достаточно надежные и, по возможности, далеко отстоящие друг от друга. Будем считать, что это x₁ и x_k. арифметическое, среднее геометрическое и среднее гармоническое . По вычисленным значениям независимой переменной находим из статистических данных соответствующие значения переменной , , для пока еще неизвестной аналитической зависимости y=f(x,a,b). Вычислим среднее арифметическое крайних значений , среднее геометрическое и среднее гармоническое

Следующая теорема позволяет определить приближение к функциональной зависимости статистических данных социальных выплат страховой компании.

Теорема. Пусть . Тогда

1. если e=e₁, то в качестве аналитической зависимости для данного графика хорошим приближением служит линейная функция ;

2. если e=e₂, то в качестве аналитической зависимости для данного графика хорошим приближением служит показательная функция;

3. если e=e₃, то в качестве аналитической зависимости для данного графика хорошим приближением служит дробно-рациональная функция ;

4. если e=e₄, то в качестве аналитической зависимости для данного графика хорошим приближением служит логарифмическая функция;

5. если e=e₅, то в качестве аналитической зависимости для данного графика хорошим приближением служит степенная функция:

6. если e=e₆, то в качестве аналитической зависимости для данного графика хорошим приближением служит гиперболическая функция

7. если e=e₇, то в качестве аналитической зависимости для данного графика хорошим приближением служит дробно-рациональная функция .

Доказательство теоремы можно найти в разных учебниках по таким направлениям как «Численные методы», «Математический анализ», «Теория вероятностей и математическая статистика».

Проводя сравнение, получаем . Следовательно, в качестве аналитической зависимости следует выбрать логарифмическую функцию . Для уточнения коэффициентов выбранной аналитической зависимости (4) воспользуемся методом наименьших квадратов. Аналогично, вычислениям, проводимым при рассмотрении дохода добровольного личного страхования, находим a=-332419

и b=165,7233

. Таким образом, подставляя найденные коэффициенты в выражение (4), получаем аналитическое выражение эмпирической функции прочих доходов

.

Список литературы

1. Данилина Н.И. и др. Численные методы.

2. Малыхин В.И. Финансовая математика. –М.:Юнити, 2003. -237 с.

3. Волков И., Загоруйко Е. Исследование операций. М-2002.

4. Искакова А.С. Условие существования оценок максимального правдоподобия для параметров одного класса многомерных распределений // Известия МОН РК, НАН РК. 2004 г. №1. – С. 90-95.

5. Ледерман Э., Справочник по прикладной статистике т.2, – М., Финансы и статистика. 1990