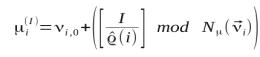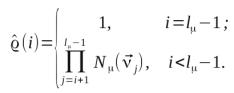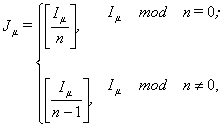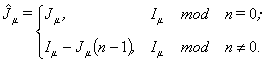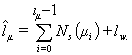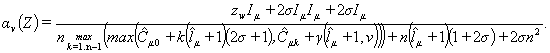Математика / 4. Прикладная математика

к.т.н. Крючин О.В., Крючина Е.И.

Тамбовский государственный университет им. Г.Р. Державина, Россия

Построение аналитической модели информационного процесса подбора активационных функции искусственной нейронной сети при использовании большого числа информационных ресурсов

Как показано в работах [1-2], одним из методов построения аналитической модели информационных процессов обучения искусственных нейронных сетей (ИНС) является подсчет числа мультипликативных и аддитивных операций, выполняемых при обучении. Для приведения аддитивных операций к мультипликативным вводится коэффициент [2].

Как известно, универсальный математический нейрон (элемент ИНС) содержит одну из допустимых активационных функций (каждая из которых требует определенное число мультипликативных и аддитивных операций [3]). Информационный процесс обучения ИНС содержит подбор активационной функции каждого нейрона — выбор наиболее-оптимальной из допустимого диапазона. Если обозначить набор активационных функций -го нейрона как , а размерность этого вектора, характеризующую количество активационных функций нейрона, как , то состояние -го нейрона на -ой итерации можно вычислить по формуле

	(1)

где

	(2)

Для каждого набора активационных функций подбираются значения весовых коэффициентов и вычисляется значение целевой функции (здесь — вектор активационных функций, — весовые коэффициенты, — -ое выходное вектора моделируемого объекта, — количество строк в обучающей выборке, — количество выходов объекта, а F — функция, вычисляющая выходные значения ИНС)

(3)

Общее количество итераций информационного процесса обучения вычисляется по формуле

.	(4)

Следовательно, количество операций информационного процесса подбора активационных функция выражается как

	(5)

где — количество операций, необходимых для подбора весовых коэффициентов [3-4].

Повышение эффективности информационного процесса подбора активационных функций заключается в использовании набора элементов информационных ресурсов (ИР-элементов), в качестве которых могут выступать узлы кластерной системы или вычислительной сети. При использовании ИР-элементов каждый из них, за исключением нулевого, перебирает

	(6)

вариантов, а нулевой —

	(7)

Таким образом, на ведущем ИР-элементе алгоритм следующий: 1) формирование структур для неуправляющих ИР-элементов; 2) рассылка структур на ИР-элементы; 3) перебор всех возможных вариантов из имеющихся на данном ИР-элементе и выбор оптимального набора активационных функций и связанной с ним погрешности; 4) получение с ИР-элементов наилучшего вектора активационных функций и соответствующего ему значения невязки; 5) выбор наименьшего значения невязки. Для неуправляющего ИР-элемента алгоритм другой: 1) получение структуры; 2) перебор всех возможных вариантов и выбор оптимальных значений активационных функций и связанной с ними погрешности; 3) отправка на ведущий ИР-элемент значений активационных функций и погрешности [3-4].

Если обозначить количество элементов -го нейрона как , то по формуле

	(8)

можно выразить общее количество элементов в сети. Таким образом, информационный процесс подбора активационных функций требует

	(9)

операция, где , Следовательно, эффективность параллельного информационного процесса обучения можно выразить как

	(10)

Таким образом, аналитическая модель может быть выражена формулой

	(11)

Используемая литература

1. Oleg V. Kryuchin, Alexander A. Arzamastev, Prof. Dr. Klaus G. Troitzsch (2011): Comparing the efficiency of serial and parallel algorithms for training artificial neural networks using computer clusters, Arbeitsberichte aus dem Fachbereich Informatik, 13/2011, Universität Koblenz-Landau, ISSN (Online) 1864-0850. http://http://www.uni-koblenz.de/~fb4reports/2011/2011_13_Arbeitsberichte.pdf.

2. Крючин, О.В. Сравнение эффективности последовательных и параллельных алгоритмов обучения искусственных нейронных сетей на кластерных вычислительных системах / О.В. Крючин, А.А. Аразмасцев // Вестн. Тамб. ун-та. Сер. Естеств. и техн. науки. 2010. — Т. 15, Вып. 6 — С. 372-375.

3. Крючин, О.В. Нейросетевой симулятор с автоматическим подбором активационных функций / О.В. Крючин // М.: Информационные технологии. — 2010. — №7 — С. 47-52.

4. Oleg V. Kryuchin, Alexander A. Arzamastsev, Prof. Dr. Klaus G. Troitzsch (2011): A parallel algorithm for selecting activation functions of an artificial network, Arbeitsberichte aus dem Fachbereich Informatik, 12/2011, Universität Koblenz-Landau, ISSN (Online) 1864-0850 http://www.uni-koblenz.de/~fb4reports/2011/2011_12_Arbeitsberichte.pdf.

5. Крючин, О.В. Параллельные алгоритмы обучения искусственных нейронных сетей / О.В. Крючин // Информационные технологии и математическое моделирование (ИТММ-2009) : матер. VIII Всерос. науч.-практ. конф. с междунар. участием, 12-13 ноября 2009 года. — Томск:, 2009. — Ч. 2. — С. 241-244.