УДК 539.23
А. И.
Моисеева, О.С. Баруздина, А. Р. Байджанов
Череповецкий государственный университет
Моделирование процесса полимеризации.
Образование полимерной цепи можно
разделить на четыре стадии: инициирование, рост, обрыв и передача цепи.
Инициация вызывается свободными радикалами, которые можно получить или из
самого мономера, или путем добавления вещества-инициатора. Затем начинается
рост цепи: свободный радикал атакует молекулу мономера, при этом за счет
разрушения двойной связи в мономере образуется свободный радикал большего
размера, который, в свою очередь, снова атакует молекулу мономера, тем самым
увеличивая цепь еще на одно звено и образуя макрорадикал. Рост цепи продолжается
по этому сценарию вплоть до ее обрыва, который может быть спровоцирован двумя
реакциями – либо отщеплением атома водорода одним макрорадикалом от другого
(реакция диспропорционирования), либо объединением двух макрорадикалов в одну
молекулу (рекомбинация). При передаче цепи макрорадикал реагирует с молекулой
примеси, образуя неактивную макромолекулу и новый свободный радикал, который
может снова инициировать полимеризацию. Передача цепи часто используется для
ингибирования радикальной полимеризации или получения разветвленных
макромолекул [1].
Вполне очевидно, что образующийся в ходе
радикальной полимеризации полимер не будет являться однородным, а, скорее,
будет смесью различных макромолекул, различных по составу, ведь на реакции,
происходящие с макрорадикалами, влияют случайные факторы. В связи с этим, для
описания кинетической схемы были введены усредненные величины и сделан ряд
допущений. Величину, которая обозначает количество мономеров, образовавших одну
макромолекулу, называют средней степенью полимеризации. Для расчета средней
степени и скорости полимеризации введены следующие допущения, упрощающие
расчет: суммарная скорость изменения концентрации всех макрорадикалов всегда
меньше скорости их образования; способность вызвать реакцию одинакова как для
первичного радикала, так и для макрорадикала, то есть не зависит от размера
радикала; расход мономера при инициации и передаче цепи столь незначителен, в
сравнении с ростом цепи, что не учитывается; при реакции передачи цепи
активность радикала остается той же. Принимая во внимание эти допущения и
учитывая возможность рекомбинации первичных радикалов с вводом коэффициента
эффективности инициирования ![]() , используя интегральный метод, было выведено уравнение для скорости
радикальной полимеризации, которое имеет следующий вид:
, используя интегральный метод, было выведено уравнение для скорости
радикальной полимеризации, которое имеет следующий вид:
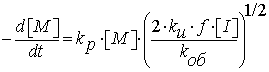 ,
(1.1)
,
(1.1)
где ![]() и
и ![]() - концентрации
мономера и инициатора соответственно,
- концентрации
мономера и инициатора соответственно, ![]() - константа
скорости реакции,
- константа
скорости реакции, ![]() - константа
скорости инициации,
- константа
скорости инициации, ![]() - константа
скорости обрыва цепи,
- константа
скорости обрыва цепи, ![]() - коэффициент
эффективности инициирования,
- коэффициент
эффективности инициирования, ![]() - скорость
изменения концентрации мономера, или скорость роста цепи.
- скорость
изменения концентрации мономера, или скорость роста цепи.
Из уравнения (1.1) видно, что скорость
радикальной полимеризации пропорциональна начальной концентрации мономера и
корню квадратному из начальной концентрации инициатора, и также определяется
соотношением элементарных констант. Концентрации, в свою очередь, будут
зависеть от температуры и от времени, но эти зависимости вывести уже сложнее.
В ходе решения (1.1) рассмотрен
случай, когда ![]() зависит от температуры.
Чтобы учесть эту зависимость и выразить зависимость константы скорости реакции
от температуры, воспользуемся уравнением Аррениуса:
зависит от температуры.
Чтобы учесть эту зависимость и выразить зависимость константы скорости реакции
от температуры, воспользуемся уравнением Аррениуса:
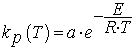 , (1.2)
, (1.2)
![]() и
и ![]() - константы для
данной реакции,
- константы для
данной реакции, ![]() - универсальная газовая постоянная.
- универсальная газовая постоянная.
Подставив уравнение (1.2) в (1.1),
получим:
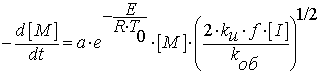 (1.3)
(1.3)
Так как (1.3) - обыкновенное
дифференциальное уравнение первого порядка, мы можем численно решить его,
воспользовавшись встроенными функциями пакета Mathcad [2]. Оставшиеся неизвестные константы выбираем
произвольно. В уравнении Аррениуса температуру можно задавать различными
способами.
Рассмотрен случай, когда процесс
полимеризации протекает при постоянной температуре, и построены графики роста
продукта реакции при приведённых температурах ![]() ;
; ![]() ;
; ![]() ;
; ![]() , где
, где ![]() ‒ температура, при которой полимеризация уже может
происходить, так называемая температура полимеризации.
‒ температура, при которой полимеризация уже может
происходить, так называемая температура полимеризации.
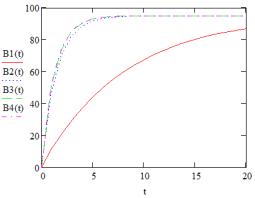
Рис. 1. Сравнительный график скорости роста цепи для разных постоянных температур при радикальной полимеризации.
Как видно из графика, чем выше температура
– тем быстрее протекает процесс полимеризации. При низкой температуре рост
полимерной цепочки идёт, но со значительно меньшей скоростью, и цепочка не
достигнет того же размера, как при высокой температуре.
Ниже рассмотрен случай, когда полимеризация происходит в
нагревающейся печи, где температура возрастает по линейному закону и ![]() зависит от
температуры. Представив
зависит от
температуры. Представив ![]() как линейную
зависимость и подставив её в уравнение Аррениуса, получим график для скорости
роста цепи. Возьмём три разных линейных уравнения для температур, с одинаковым
начальным значением, но возрастающих с разной скоростью (
как линейную
зависимость и подставив её в уравнение Аррениуса, получим график для скорости
роста цепи. Возьмём три разных линейных уравнения для температур, с одинаковым
начальным значением, но возрастающих с разной скоростью (![]()
![]()
![]()
![]() ).
).
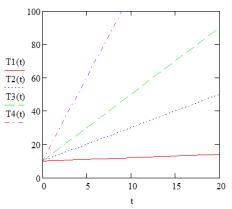
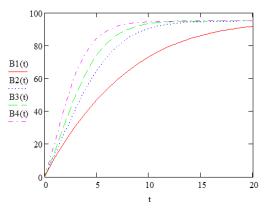
Рис. 2. Сравнительный график скорости роста цепи для разных температур, заданных как линейные функции, при радикальной полимеризации
Можно сделать вывод, что при линейном задании температуры, в зависимости от
скорости нагревания, полимеризация протекает тем быстрее, чем идёт нагрев.
Проверено, влияет ли начальная
температура, от которой идёт нагревание, на результаты реакции (![]()
![]() 0
0 ![]()
![]() ).
).
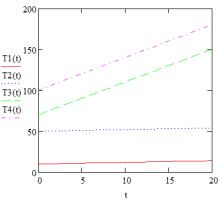
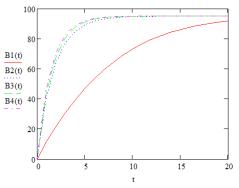
Рис. 3. Сравнительный график скорости роста цепи при радикальной полимеризации для разных температур, заданных как линейные функции, при различных начальных условиях
Можно сделать вывод, что разная скорость
нагревания для линейного вида уравнения температуры оказывает значительное
влияния на скорость роста полимерной цепи, при условии, если начальная
температура будет одинакова. Если же начальная температура будет отличаться,
то, как и для случая постоянной температуры, полимеризация быстрее пройдёт в
изначально более нагретой печи.
Рассмотрен случай, когда полимеризация
протекает при температурах, меняющихся
от одного одинакового значения до другого различными способами за одинаковое
время (![]()
![]()
![]() ).
).
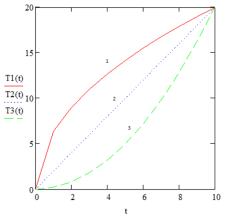
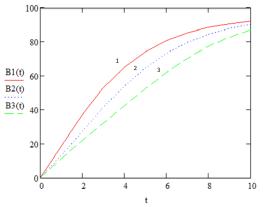
Рис. 4. Сравнительный график скорости роста цепи для температур, заданных различными функциями, при радикальной полимеризации
Исходя из полученных графиков, можем
сделать вывод, что скорость
полимеризации зависит не только от самого значения температуры, но и способа её
задания, таким образом, полимеризация зависит от температуры как функционал.
Важно понимать, что все вышеизложенные
результаты в этом пункте получены в ходе рассмотрения общего случая, и все
константы выбирались произвольно. При проверке, можно ли использовать
рассматриваемую схему при получении реально существующего полимера, были
использованы данные для распространённого мономера стирола, используемого для
получения полимера полистирола. Для стирола константа скорости реакции ![]() составит
составит ![]() , а энергия активации
, а энергия активации ![]() .
.
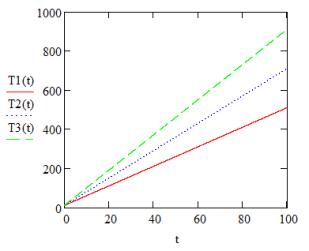
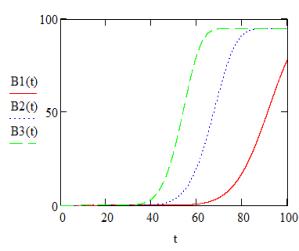
Рис. 5. Сравнительный график скорости роста цепи полистирола при температурах, заданных линейно.
Как видно из графиков на рисунке 7,
полимеризация стирола идёт тем быстрее, чем быстрее повышается температура, что
совпадает с уже рассмотренным общим случаем. В дальнейшем ходе работы константы
снова будут выбираться произвольно. Это связано с тем, что целью исследования
является определить общий характер зависимости процесса полимеризации от
температуры, а не рассмотреть какой-либо конкретный полимер.
Используемая литература:
1.
Берлин А.А., Вольфсон
С.А., Ениколопян Н.С. Кинетика полимеризационных процессов. - М.: Химия, 1978.
– 320 с.
2.
Максимова О.Г., Максимов
А.В., Петрова Т.О. Вычислительная физика и компьютерное моделирование
лабораторный практикум. – Череповец, 2011