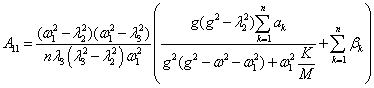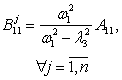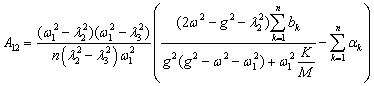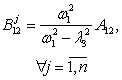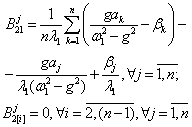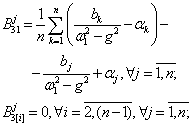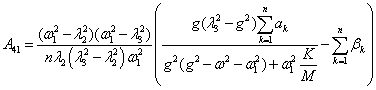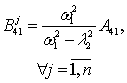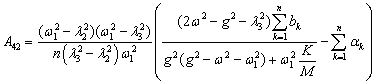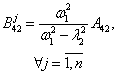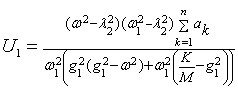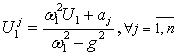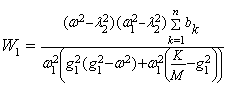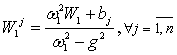Докукова Н.А., Конон Н.П., Конон П.Н.

Белорусский государственный университет

ВЛИЯНИЕ ВНЕШНЕГО НАГРУЗОЧНОГО РЕЖИМА НА СИНХРОННЫЕ ДВИЖЕНИЯ СИСТЕМЫ АВТОНОМНЫХ ОСЦИЛЛЯТОРОВ

В работе исследуется динамическая система на рисунке 1, с n автономными осцилляторами, взаимодействующими между собой посредством общей связи, каждый из которых испытывает внешнее гармоническое воздействие одинаковой частоты и с разными начальными фазами. Записаны уравнения движения (1), получены точные аналитические формулы колебательных режимов n тел, по методике, развитой авторами в [1, 2], проведены численно-аналитические расчеты. Результаты сопоставлены с экспериментальными данными [3].

Полученные результаты могут быть использованы для решения различных прикладных задач механики, радиоэлектроники, электрорадиоцепей, лазерной физики, радиолокации и радионавигации, современных систем радиосвязи, определения координат объектов GPS, слежения за объектами на поверхности Земли и в околоземном пространстве.

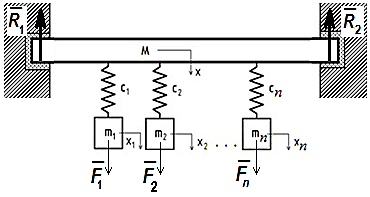
Рисунок 1 - Схема колебаний n - осцилляторов на закрепленной балке

Система уравнений движения механической системы, в матричной форме:

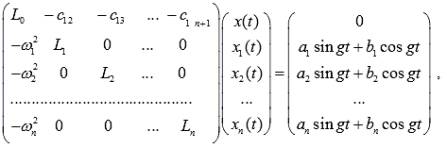
(1)

с начальными условиями

, , (2)

, _. (3)

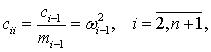
Здесь , − дифференциальные операторы по параметру времени t ; c_ij – коэффициенты упругих элементов c_j-1, отнесенных к соответствующим массам m_i-1, , , b – коэффициент вязкого сопротивления колебаниям балки; – вектор искомых перемещений масс на рисунке 1; – вектор виброускорений нагрузочного режима; , ; – гармонические силы , являющиеся внешними и приложены к автономным осцилляторам; и – силы линейного трения и упругого «винклеровского» основания в опорах балки . Общая сила - консервативная, сила линейного трения в балке, неконсервативная сила вязкого сопротивления колебаниям - .

Характеристическое уравнение примет вид

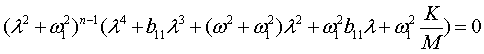, (4)

если парциальные частоты всех n-линейных осцилляторов одинаковы . Для простоты положим b = 0 . Тогда решения многоэлементной задачи приводятся к следующим колебательным режимам

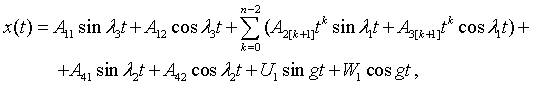(5)

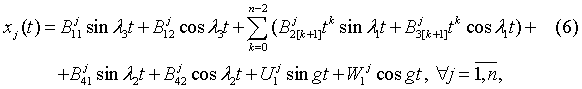
где l₁=w₁, 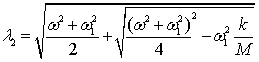,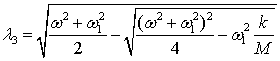. Неопределенные коэффициенты соответствующих решений находятся по методике, развитой в [1, 2], аналитические формулы для которых сведены в таблицу 1.

Таблица 1

Номер группы коэффициентов	Коэффициенты перемещения балки x(t)	Коэффициенты перемещений автономных осцилляторов xj(t),
1	2	3
1
2
3
4
5

Если положить n = 2 , с₁₂ = с₁₃ , a₁ = a₂ = b₁ = b₂ = b = K = 0 и выбрать в качестве начальных условий следующие: a₁ = g, a₂ = d, b₁ = b₂ = 0, то получаются аналитические формулы решений, полностью совпадающие с перемещениями в [2].

В качестве примера рассмотрим механизм с произвольными физическими параметрами: n = 4, M = 20.0 кг, m₁ = m₂ = m₃ = m₄ = 2.0 кг, c₁=c₂=c₃=c₄= 55.0н/м,
K = 10.0 н/м, a₁ = -0.05 м, a₂ = 0.07 м, a₃ = 0.03 м, a₄ = -0.01 м, b₁ = 0.3 м/c,
b₂= 0.6 м/c, b₃ = 0.1 м/c, b₄ = 0.9 м/c, g = 40p рад/с, w = 3.3912 рад/с, w₁=5.244рад/с, l₁= 5.244 рад/с, l₂ = 6.2164 рад/с, l₃ = 0.5965 рад/с, F₁ = 23.13 н, F₂=16.87н,
F₃ = 15.48 н, F₄ = 15.68 н, a₁ = 1.2 м/с², a₂ = 8.3 м/с², a₃ = 4.2 м/с², a₄=3.1м/с²,
b₁ = 11.5 м/с², b₂ = 1.5 м/с², b₃ = 6.5 м/с², b₄ = 7.2 м/с². Перемещения и скорости элементов представлены на графиках рисунка 2 и на основании формул (5), (6), таблицы 1 примут вид:

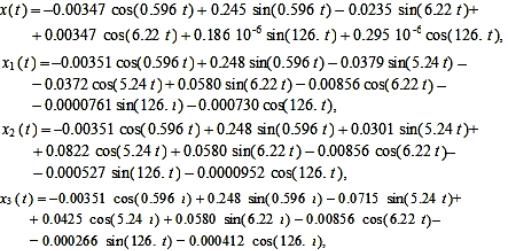
(7)

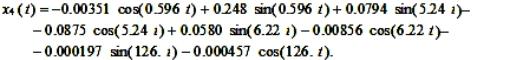
а) б)

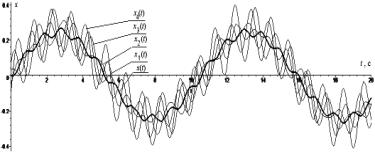
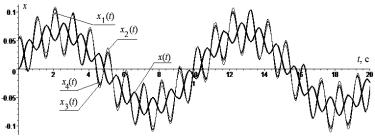
Рисунок 2 - Перемещения x(t) и x_j(t) , j = динамической системы, состоящей из 4 одинаковых осцилляторов на упругой балке с разными начальными условиями на а и скорости v(t), v_j(t) на б

На рисунке 2 очевидно рассогласование по фазам колебаний гармонических осцилляторов и явное отличие по амплитудам. Более синхронизированной данная система станет, если в формулах таблицы 1 положить все начальные условия a_j и b_j, j=, одинаковыми при несущественном влиянии внешних сил. Например, a_j=0.05 м, b_j = 0.1 м/с j = .

(8)

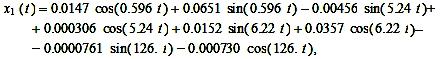
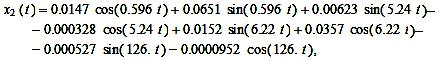
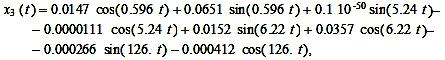
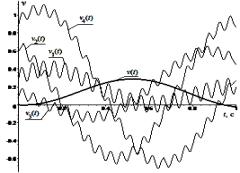
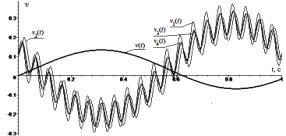
На рисунках 2 и 3 можно наблюдать полное соответствие начальным условиям (2), (3) и справедливость выведенных формул, представленных в таблице 1.

а) б)

Рисунок 3 - Перемещения x(t) и x_j(t), j = четырех одинаковых осцилляторов динамической системы с одинаковыми начальными условиями на а и скорости v(t), v_j(t) на б

Выводы. На основе развитой авторами методики [1, 2] решения динамических задач многоэлементных механических систем со специальными нагрузочными режимами получены аналитические формулы колебаний произвольного числа n линейных осцилляторов на общей жесткой связи, сведенные в таблицу 1. Они позволяют легко управлять свойствами синхронизируемых явлений, наперед определять и задавать его характеристики, устанавливать зависимости между параметрами, обеспечивающими «синфазную» однонаправленную синхронизацию, противофазную или иные виды динамических взаимосвязей между телами. На основании формул (5), (6), таблицы 1 и представленных расчетов можно сделать вывод о том, что синхронными будут колебания всех элементов механической системы с одинаковыми отклонениями и скоростями в начальный момент времени a_j = a₀, b_j = b₀, j = , если влияния внешних сил являются несущественными, обладающими высокими частотами и малыми величинами амплитуд. Это очевидно проиллюстрировано на графиках рисунка 3, на которых колебательные режимы x_j, j = , практически совпали.

Литература

1. Dokukova N. A. and Konon P. N. General laws governing in mechanical vibratory systems// Journal of Engineering Physics and Thermophysics, 2006, Volume 79, Number 4, Pages 824-831, Publisher Springer New York, ISSN: 1062-0125.

2. Dokukova N.A., Kaftaikina E.N. The synchronization of two linear oscillators// Materialy VII miedzynarodowej naukowi-praktycznej konferencji. Przemysl, Polska. 7-15 listopada 2012 r. Przemysl: Nauka i studia, Vol. 18, pp. 28 – 35, 2012.

3. Пиковский A.C. Синхронизация: Фундаментальное нелинейное явление / A.C. Пиковский, М.Г. Розенблюм, Ю. Курте. - М.: Техносфера, 2003. - 494 с.