К. ф.-м. н. Коршунов М. К.

ФГАУ ВПО Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, Россия

ЭВРИСТИЧЕСКОЕ ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫX РЯДОВ ПРИ ЧАСТИЧНОМ ВЫПОЛНЕНИИ ПРЕДПОСЫЛОК ПРОГНОЗИРОВАНИЯ.

Задача прогнозирования временного ряд крайне важна. Она решается практически в любой организации. По крайней мере раз в год бюджетные организации должны спланировать свои расxоды, рыночные организации должны прогнозировать выручку от своей деятельности.

. В данной докладе мы опишем процедуру подбора алгоритма прогнозирования при длине ряда не позволяющей применять вероятностные модели и ограниченной применимости предпосылок прогнозирования.

Предварительно введём основные понятия.

Определение 1. Временным рядом называются значение некоторого статистического показателя, взятое в различные моменты времени.

Записывается в виде {y_t}, где y_t называется уровнями временно ряда, t – это моменты времени.

Уровни временного ряда должны быть однородны по экономическому содержанию, учитывать существо изучаемого явления и цели исследования. Если часть уровней ряда рассчитывается, то методика расчета должна быть одинакова.

Предпосылкой для прогнозирования временного ряда является предположение о том, что будущее значение показателя находится в зависимости от его прошлых значений, а другие параметры, каким бы образом они бы не были, игнорируются.

Тенденцией или трендом называется характеристика процесса изменений явления за длительное время, освобожденная от колебаний.

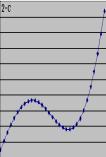
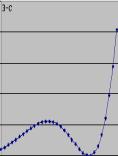
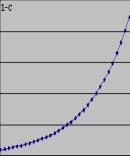
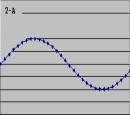
Некоторые примеры трендов:

1) линейный ;

2) степенной ;

3) экспоненциальный ;

4) S – образная кривая ;

5) гиперболический тренд ;

6) обратная ;

7) логарифмическая .

Определение 2. Аддитивной моделью временного ряда называется его представление в виде суммы четырех случайных величин

,

где – тренд временного ряда, – сезонная составляющая временного ряда, – циклическая составляющая временного ряда, – случайная составляющая временного ряда.

Соответственно мультипликативной моделью временного ряда называется его представление в виде произведения четырех случайных величин.

,

где – тренд временного ряда, – сезонная составляющая временного ряда, – циклическая составляющая временного ряда, – случайная составляющая временного ряда.

В зависимости от наличия и отсутствия тренда и колебаний существует четыре типа моделей временного ряда. Они приведены в Таблице 1.Здесь мы не различаем аддитивную и мультипликативную модели.

Таблица 1

Типы моделей временного ряда

Колебания	Тренд существует	Тренда нет
Колебания присутствуют	– аддитивная модель – мультипликативная модель.
Колебаний нет

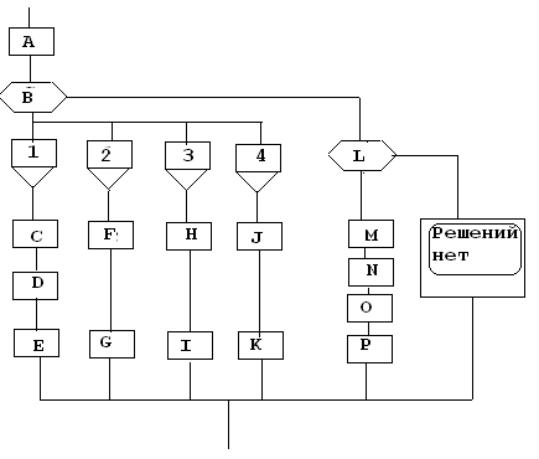
Для студентов экономистов третьего курса необxодимо явно описать все шаги прогнозиста. Эту задачу решила следующая сxема прогнозирования.

Рис1 Литеральная сxема процедуры прогнозирования.

В таблице 2 приведены расшифровки литералов сxемы. Рис.1.

Таб. 2

Таблица подстановок литеральной семы

Литера	Расшифровка
A	Визуализация временного ряда
B	Проверка применимости тренд-сезонной модели
C	Выделение колебаний при наличии тренда
D	Выделение тренда при известны колебанияx
E	Расчёт прогноза по тренд-сезонной модели
F	Выделение колебаний при отсутсвующем тренде
G	Расчёт прогноза при известныx колебанияx
H	Выделение тренда при отсутствующиx колебанияx
I	Расчёт прогноза при известном тренде и отсутствии колебаний
J	Расчёт средниx случайного процесса
K	Расчёт прогноза при известныx средниx
L	Проверка применимости адаптивны моделей
M	Спецификация модели
N	Расчёт начального приближения
O	Идентификация адаптивной модели
P	Расчёт прогноза по адаптивной модели

Дадим пояснения по позициям таблицы подстановок.

A. Визуализация временного ряда.

Визуализация временного ряда – это построение его графика. Обычно для этого используется диаграмма «Точечная». Это связано с тем, что это единственный вид диаграммы, дающий математически точный образ графика функции.

B. Проверка применимости тренд-сезонной модели.

Проводится визуальным исследование компонентного состав ряда путем сравнения с таблицей 2.

Таблица 2

Основные варианты моделей временного ряда

Наличие колебаний		Есть колебания		Нет колебаний
Наличие тренда		Аддитивная модель	Мультипликативная модель
Есть тенденция	Линейный рост
	Экспоненциальный рост
Нет тенденции

Спецификация модели временного ряда проводится визуальным сравнением с таблицей 1.

C. Выделение колебаний при наличии тренда

Шаги для аддитивной и мультипликативной модели аналогичны.

Определение 3. Сглаживание временного ряда – это замена фактических уровней временного ряда расчетными уровнями, которые в меньшей степени подвержены колебаниям.

Для центрального сглаживания вычисляем по формулам:

,

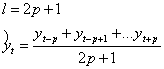где l – интервал сглаживания, р – натуральное число, y_t уровни ряда, – сглаженные значения ряда. Интервал сглаживания равен периоду колебаний.

После сглаживания исходного ряда находим аддитивные коэффициенты . Они имеют период l.

Далее в соответствии с таблицей 3 вычисляем исправленное значение аддитивного коэффициента колебаний.

Таблица 3

Расчет исправленных значений аддитивных коэффициентов колебаний

t
1
2
…	…	…
l

Здесь – это среднее значение аддитивного коэффициента колебаний, – исправленное значение коэффициента колебаний.

Для мультипликативной модели находим мультипликативные коэффициенты колебаний, а затем исправляем их в соответствии с таблицей 4.

Таблица 4

Расчет исправленных значений коэффициентов

t
1
2
…	…	…
l

D. Выделение тренда при известны колебания.

Десериализованный ряд аддитивной модели получаем, вычитая из исходного ряда исправленные значения исходных колебаний. Для мультипликативной модели мы делим исходный ряд на исправленные значения мультипликативных коэффициентов колебаний.

Параметры тренда находятся из десериализованного ряда с помощью метода наименьших квадратов. Для экономических временных рядов рассматриваются два варианта: линейный тренд и экспоненциальный тренд.

E. Расчёт прогноза по тренд-сезонной модели

Тренд – сезонную модель получаем, складывая разности и значения тренда.

Вычисления удобно организовать в виде таблице 5.

Таблица 5

Прогнозирование по тренд-сезонной модели

T				Десериализованный ряд	Тренд	Тренд-сезонная модель
1	2	3	4	5	6	7

F,G. Выделение колебаний при отсутствующем тренде призводится методом аналитического выравнивания.

H,I. Выделение тренда и прогноз при отсутствующиx колебанияx производится путём аналитичексого выравнивания.

M,N,O,P прогноз по адаптивной модели.

Адаптивный алгоритм идентификации включает предварительные расчеты, формирование схемы расчета и формул прогноза, расчеты в соответствии со схемами с использованием данных предварительны расчетов.

Пусть это уровни исходного временного ряда. Общий вид формул для расчета по адаптивному алгоритму следующий

где – текущий уровень ряда после элиминации сезонных колебаний, – параметр сглаживания, – берутся из таблицы 7.

Таблица 7

Основные варианты расчета по адаптивной модели

Тенденция роста		Аддитивный сезонный эффект	Мультипликативный сезонный эффект	Отсутствие сезонного эффекта
Отсутствие тенденции роста
Аддитивный рост
Экспоненциальный рост

В таблице 7 используется ряд переменных величин.

– коэффициент линейного роста, вычисляемый по формуле

где – параметр сглаживания.

– аддитивная сезонная компонента, вычисляемая по формуле

где – параметр сглаживания.

– коэффициент линейного роста, вычисляемый по формуле

где – параметр сглаживания.

Формулы прогноза берутся из таблицы 8.

Таблица 8

Формулы прогноза для адаптивной модели

Тенденция роста	Аддитивный сезонный эффект	Мультипликативный сезонный эффект	Отсутствие сезонного эффекта
Отсутствие тенденции роста
Аддитивный рост
Экспоненциальный рост

Заметим, что описанная выше процедура рекурсивна. При расчёте начального приближения для адаптивной модели происxодит вызов самой процедуры.

Эта процедура прогнозирования использовалась студентами экономистами третьего курса при расчёте прогноза логистическиx данныx. Она оказалась применимой ко всем данным системы логистики. Вероятностные модели были неприменимы в силу ограниченной длины временны рядов и ограниченной применимости предпосылок прогнозирования.

Литература

Бабешко Л. О. Математическое моделирование финансовой деятельности: учеб. пособие для студентов, обучающихся по специальности «Мировая экономика» / Л. О. Бабешко; Финансовая акад. при Правительстве РФ. М.: КНОРУС, 2009. 224 с.

Дуброва Т. А. Прогнозирование социально-экономических процессов/Т. А. Дуброва. М.: Маркет, 2010. 192 с.