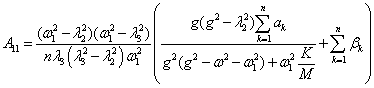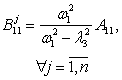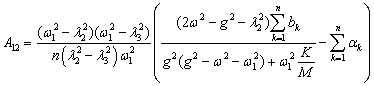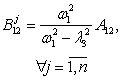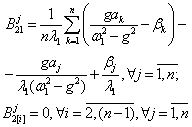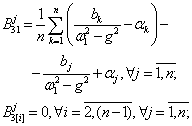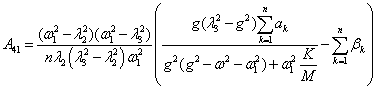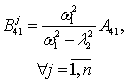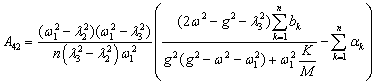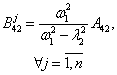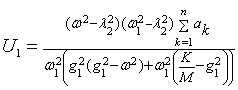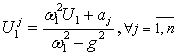Докукова Н.А., Кафтайкина Е.Н., Конон П.Н.

Белорусский государственный университет

ИССЛЕДОВАНИЕ СИНХРОННИЗАЦИИ ДВИЖЕНИЙ НЕСКОЛЬКИХ ОСЦИЛЛЯТОРОВ С ОДИНАКОВЫМИ СОБСТВЕННЫМИ ЧАСТОТАМИ

Рассматривается динамическая система с большим числом n автономных осцилляторов, взаимодействующих между собой посредством общей связи, рисунок 1. Каждый осциллятор испытывает внешнее гармоническое воздействие одинаковой частоты и разными начальными фазами.

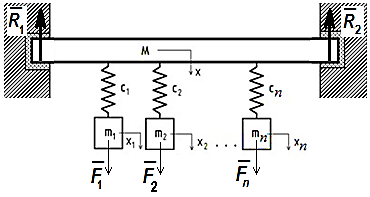
Рисунок 1 - Схема колебаний n - осцилляторов на закрепленной балке

Система уравнений движения механической системы, представленной на схеме рисунка 1, в матричной форме примет вид:

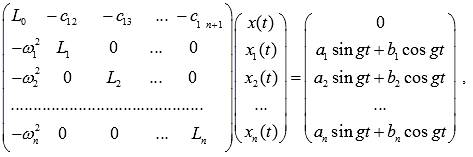
(1)

с начальными условиями

, , (2)

, _. (3)

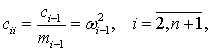
Здесь , − дифференциальные операторы по параметру времени t ; c_ij – коэффициенты упругих элементов c_j-1, отнесенных к соответствующим массам m_i-1, , , b – коэффициент вязкого сопротивления колебаниям балки; – вектор искомых перемещений масс на рисунке 1; – вектор виброускорений нагрузочного режима; , ; – гармонические силы , являющиеся внешними, приложены к автономным осцилляторам; и – силы линейного трения и упругого «винклеровского» основания в опорах балки . Общая сила - консервативная, сила линейного трения в балке, неконсервативная сила вязкого сопротивления колебаниям - .

Характеристическое уравнение примет вид

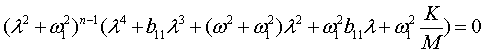, (4)

если парциальные частоты всех n-линейных осцилляторов одинаковы . Для простоты положим b = 0 . Тогда решения многоэлементной задачи приводятся к следующим колебательным режимам

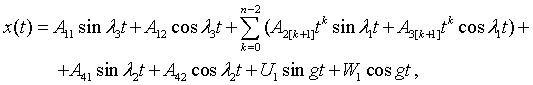(5)

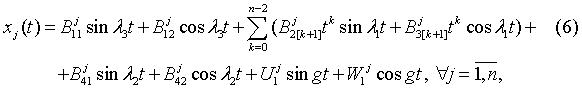
где l₁=w₁, 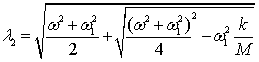,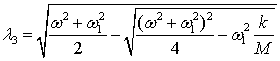. Неопределенные коэффициенты соответствующих решений находятся по методике, развитой в [1, 2], аналитические формулы для которых сведены в таблицу 1.

Таблица 1

Номер группы коэффициентов	Коэффициенты перемещения балки x(t)	Коэффициенты перемещений автономных осцилляторов xj(t),
1	2	3
1
2
3
4
5

Разностью фаз Δj = j₁ − j₂ называют разность начальных фаз j₁, j₂ двух гармонических колебаний одинаковой частоты y₁= sin(ωt + j₁), y₂=sin(ωt + j₂). Оценка величины разности фаз относится к параметрам взаимодействия сигналов. Если j₁ и j₂ постоянны во времени, то Δj от времени не зависит. При Δj = 0 колебания считаются синфазными, при Δj = π – противофазными, а при Δj = π/2 или 3π/2 − колебания находятся в квадратуре.

Положим, что влияния внешних сил , приложенных к автономным осцилляторам; являются несущественными, обладающими высокими частотами и малыми величинами амплитуд. Рассмотрим каковы при этом могут быть разности фаз j_{j -} j_i между гармоническими колебаниями осцилляторов с одинаковыми собственными частотами l₁. Соответствующее решение представимо в виде

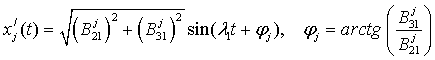_{. (7)}

Для того, чтобы между фазами была разность π, необходимо, чтобы одна из фаз j_j , другая j_i. Это возможно при и любыми числами разного знака, например,

_{. (8)}

Если , тогда противофазность наступит при условии одинаковых по модулю соответствующих коэффициентов , но всегда разных по знаку

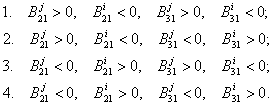(9)

В качестве примера рассмотрим механизм с произвольными физическими параметрами: n = 4, M = 25.0 кг, m₁ = m₂ = m₃ = m₄ = 2.1 кг, c₁=c₂=c₃=c₄= 74.0н/м, K = 10.0 н/м, a₁ = -0.005 м, a₄ = 0.009 м, b₁ = 0.03 м/c, b₄ = 0.09 м/c, g = 40p рад/с, w= 3.4986 рад/с, w₁=5.9362рад/с, l₁= 5.9362 рад/с, l₂= 6.8687 рад/с, l₃=0.5466рад/с, F₁ = 23.13 н, F₂=16.87н, F₃ = 15.48 н, F₄ = 15.68 н, a₁ = 1.2 м/с²,
a₂ = 8.3 м/с², a₃ = 4.2 м/с², a₄=3.1м/с², b₁ = 11.5 м/с², b₂ = 1.5 м/с², b₃ = 6.5 м/с²,
b₄ = 7.2 м/с². Удовлетворяя одному из условий противофазности (9) выберем вариант 2 для осцилляторов с номерами j = 2 и i = 3. Решая совместно неравенства относительно начальных условий a₂, a₃, b₂, b₃ получаем значения a₂ = -0.0653 м, a₃ = 0.07 м, b₂= 0.0746 м/c, b₃ = -0.02 м/c. Их подстановка в формулы (5), (6), таблицы 1 приводит к следующим перемещениям:

(10)

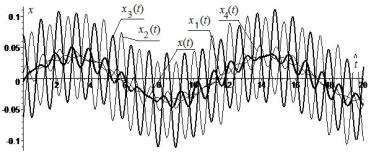
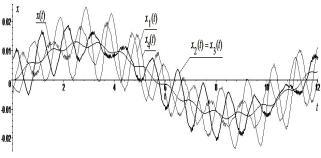
Два решения x₂(t) и x₃(t) находятся в противофазе по гармоническим колебаниям с собственной частотой l₁ = 5.94 рад/с, что можно наглядно наблюдать на графиках рисунка 2.

Для того, чтобы собственные колебания были синфазными с нулевой разностью между фазами, необходимо, чтобы выполнялось условие

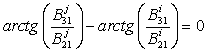_{. (11)}

а) б)

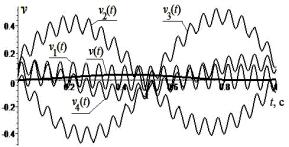
Рисунок 2 - Перемещения x(t) и x_j(t), j = , динамической системы на а, x₂(t) и x₃(t) находятся в противофазе, скорости v(t), v_j(t) на б

Это возможно, если соответствующие начальные условия (2) и (3), по крайней мере двух рассматриваемых осцилляторов, совпадали. Кроме того, должны быть одинаковыми соответствующие коэффициенты при одинаковых гармониках внешних нагрузок F_j и F_i

(12)

Рассмотрим синфазную синхронизацию двух колебательных режимов осцилляторов с номерами j = 2 и i = 3. Выберем следующие начальные условия a_j и b_j, j=: a₁ = -0.005 м, a₂ = 0.007 м, a₃ = 0.007 м, a₄ = -0.002 м, b₁ = 0.03 м/c,
b₂= -0.02 м/c, b₃ = -0.02 м/c, b₄ = -0.05 м/c, и коэффициенты при внешних нагрузках: a₁ = 1.2 м/с², a₂ = 8.3 м/с², a₃ = 8.3 м/с², a₄=3.1м/с², b₁ = 11.5 м/с², b₂ = -6.5 м/с², b₃ = -6.5 м/с², b₄ = 7.2 м/с². Получаются новые решения, синфазность которых можно наблюдать у перемещений x₂(t), x₃(t) и на графиках рисунка 3.

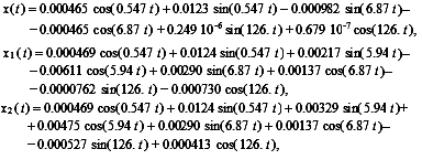
(13)

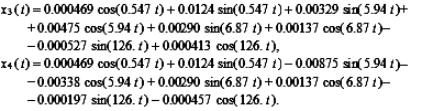
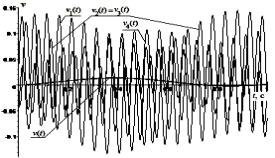
а) б)

Рисунок 3 - Перемещения x(t) и x_j(t), j = , динамической системы на а, x₂(t) и x₃(t) синфазны, с одинаковыми условиями , скорости v(t), v_j(t) на б

На рисунках 2 и 3 очевидны сходимости представленных решений по формулам (5), (6) и таблицы 1 к начальным условиям (2), (3).

Выводы. На основе развитой авторами методики [1, 2] решения динамических задач многоэлементных механических систем со специальными нагрузочными режимами получены аналитические формулы колебаний произвольного числа n линейных осцилляторов на общей жесткой связи, сведенные в таблицу 1. Получены условия, обеспечивающие фазовую, противофазовую и другие синхронизации, устанавливающие зависимости между параметрами взаимодействующих систем, если влияния внешних сил являются несущественными.

Результаты представленной работы могут быть использованы для решения различных прикладных задач механики, радиоэлектроники, электрорадиоцепей, лазерной физики, радиолокации и радионавигации, современных систем радиосвязи, определения координат объектов GPS, слежения за объектами на поверхности Земли и в околоземном пространстве.

Литература

1. Dokukova N. A. and Konon P. N. General laws governing in mechanical vibratory systems// Journal of Engineering Physics and Thermophysics, 2006, Volume 79, Number 4, Pages 824-831, Publisher Springer New York, ISSN: 1062-0125.

2. Dokukova N.A., Kaftaikina E.N. The synchronization of two linear oscillators// Materialy VII miedzynarodowej naukowi-praktycznej konferencji. Przemysl, Polska. 7-15 listopada 2012 r. Przemysl: Nauka i studia, Vol. 18, pp. 28 – 35, 2012.