Педагогические науки/ 5.Современные методы преподавания

К. пед. наук, доцент Женетль С.Н.

Майкопский Государственный Технологический Университет, Россия.

Некоторые аспекты применения

интегрального исчисления в физике.

Современный специалист должен хорошо владеть  количественными методами анализа. К такому выводу нетрудно прийти практически с самого начала изучения прикладных курсов. При этом важны знания традиционных математических курсов, но особое внимание хочется уделить дифференциальному исчислению.

Центральным понятием дифференциального исчисления являются производная и интеграл, и эти понятия тесно связаны с физиком, с законами окружающей нас природы. Именно для исследований физических задач движения планет вокруг Солнца были заложены основы дифференциального исчисления И. Ньютоном.

Традиционно практическое приложение интеграла иллюстрируется вычислением площадей различных фигур, нахождением объемов геометрических тел и некоторыми приложениями в экономике. Хотелось обратить внимание на роль интеграла в моделировании физических процессов, поскольку приложениям интеграла в физике не уделяется достаточно внимания даже при обучении студентов технических направлений. Вместе с тем, интегральное исчисление дает богатый математический аппарат для моделирования и исследования процессов, происходящих в физике.

Определение интегральной суммы позволяет использовать понятие определенного интеграла в различных разделах физики. Его применение основано на том, что любой меняющийся физический процесс может быть интерпретирован как непрерывный, приращения которого достаточны близки к нулю. 

Интегральное исчисление в физике используют для вычисления пройденного пути при неравномерном движении, массы неоднородного стержня, количества электричества при переменной силе тока, нахождение координат центра тяжести, импульса силы, энергии потенциальной и кинетической, изучения зависимости между магнитным потоком, пронизывающим проводящий замкнутый контур, и электродвижущей силой (ЭДС) индукции в этом контуре и т.д. И это далеко не полный список приложений интегрального исчисления в физике. Остановимся на нескольких примерах использования интегралов в разных разделах физики.

Определение давления жидкости на вертикальную пластинку.

Давление, производимое жидкостью с удельным весом на одну сторону погруженной в неё вертикальной пластинки, если расстояние х точек пластины до уровня жидкости изменяется от a до b, определяется по формуле

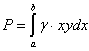(1),

а y – длина горизонтального сечения пластины.

Требуется определить величину давления воды на полукруг, вертикально погруженный в жидкость, если его радиус R, а центр находится на свободной поверхности воды.

Воспользуемся полученной формулой для нахождения давления жидкости на вертикальную пластинку. В данном случае пластинка ограничена линиями у = -, y, x = 0, x = R. Получаем:

P =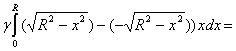

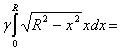
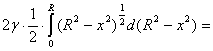
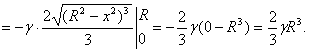
Измерение среднего времени жизни радиоактивных атомов.

Пусть имеется N(t) нераспавшихся атомов к моменту времени t. Решим дифференциальное уравнение

,

где - среднее время жизни радиоактивного атомов, при начальных условиях N=N₀ при t=0.

Получаем: , где .

Подсчитаем, сколько процентов атомов распадается за время, меньшее среднего времени жизни :

.

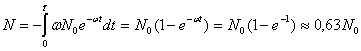Следовательно, за время меньшее, чем , распадается 63% атомов.

Вытекание воды из бака под действием силы тяжести.

Рассмотрим бак с начальным уровнем воды с небольшим отверстием вблизи дна. Требуется найти, как уровень изменяется со временем из-за вытекания воды через отверстие.

Уравнение Бернулли для уровня воды в каждый момент с записывается в виде:

Условие сохранения объёма жидкости, вытекающей за время

,

где -площадь отверстия, - площадь дна бака, - понижение уровня за время . Деля обе части на , получаем дифференциальное уравнение:

,

где .

Проинтегрируем это уравнение от до произвольного времени :

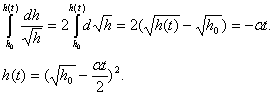
Из полученной формулы следует, что истечение воды из бака длится конечное время

Весь спектр приложений определенного интеграла в физических задачах очень широк и разнообразен, что делает необходимым при изучении математики, обратить внимание на физический смысл определенного интеграла и включение его основных приложений в курс прикладного бакалавриата.

Литература:

1. Дмитриева В.Д. Курс физики: Учебное пособие. – М.: Высш. шк., 2005.

2. Зельдович Я.Б. Высшая математика для начинающих и её приложения в физике: Учебное пособие. - М.: ФИЗМАТЛИТ, 2010.

3. Ляпунова М.Г. Приложения определенного интеграла к решению задач геометрии и физики: Учебное пособие. - Благовещенск: Амурский гос. ун-т, 2000.

4. Юмашев Д.В. Интегралы и производные в физике: Учебное пособие. - М.: ФАЛТ ФМТИ, 2006.