N.Daribayeva, A.Serikbayeva,

Kazakh National Research Technical University named after K. Satbayev, Kazakhstan, Almaty

serikbayeva05@gmail.com

Hydrodynamic modeling of a rotating filtration process

Abstract.Rotative filtration is an innovative tangential filtration process that allows

concentration or clarification of suspensions at lower cost. A rotative filter is made of two coaxial cylinders, an outer fixed cylinder and an inner porous rotating cylinder. A suspension is injected at the top of the device and flows out at the bottom. During the descent, part of the liquid is evacuated radially through the inner porous wall and the particle concentration increases. This system is already use for milk skim separation, in fermentation processes and separation of oil, biological suspension, blood plasma, and even for waste water treatment in spatial stations.[1]

The main advantage of this technology is that the presence of Taylor vortices that appear in the liquid flow if the inner cylinder rotates at sufficiently high velocity. This secondary flow, which results from a centrifugal instability may delay significantly the fouling of the filter, since it keeps the particles in motion, away from the filtering wall. As a consequence, a smaller filtering surface is necessary to attain the same performances as a static filter. From a hydrodynamic point of view, the flow in a rotating filter can be seen as the superposition of a circular Couette flow V(r), an annular Poiseuille flow and W(r) a radial flow U(r).

The objectives of this work is to study the stability of Couette-Poiseuille-radial flow and in particular the appearance of Taylor vortices. To achieve these goals, a triple approach, theoretical, numerical and experimental, will be performed. An overview of research work was made in France, Nancy in Lorraine University (ENSIC) in laboratory of Gemico under the direction of professors Cherif Nouar and CecileLemaitre.

Keywords: Non-Newtonian fluid, circular Couette flow, shear-thinning fluid, stability analysis.

A Taylor-Couette flow, the flow between a rotating inner cylinder and stationary outer cylinder becomes unstable when the rotation speed of the inner cylinder exceeds a given critical value, and this because of the centrifugal force. However, the stability is found to be impaired if one of these two cylinders is porous and a radial flow is imposed.

The study of the linear stability for the axisymmetric flows shows that a flow stream can be stabilized by: a radial flow from the outside inside and a strong radial flow, but from the inner to the outside.

On the contrary, a small radial flow of the inner cylinder to the outer cylinder can slightly destabilize the system. All physical phenomena inherent to the effects of stabilization or disturbance of the radial flow are not yet fully defined. It is therefore the superposition of a radial flow a Taylor-Couette flow between two rollers which modifies the linear system stability.

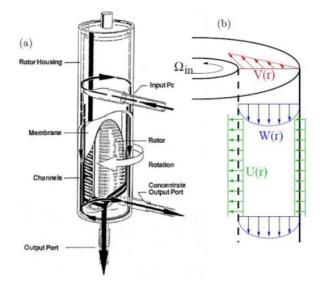
Figure 1. (a) Scheme of a rotative filter [2]. (b) In this filter, liquid flows in the axial, azimuthal and radial directions [2]

We consider the flow of a purely viscous non-Newtonian fluid between two infinitely long concentric cylinders. The inner cylinder of radius is rotating with a constant angular velocity > 0. The outer cylinder of radius is rotating with a constant angular velocity, with > 0 for co-rotating cylinders and < 0 for counter -rotating cylinders. The conservation of mass for an incompressible fluid reads:

(1.1)

And the conservation of momentum reads:

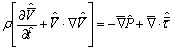(1.2)

Here s the velocity, is the pressure and is the deviactoric extra-stress tensor.

The stress tensor is expressed as a function of the

The shear rate tensor is defined with the gradient of velocity.

The associated boundary conditions reads:

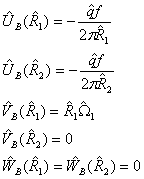
is a positive constant

Non-dimensional form of the equations

To be able to easily compare our results with those produced already in the literature, we

non-dimensionalize the equations by using the following reference scales:

- a reference viscosity

- the reference length scale

- - velocity scale

- time scale

- the quantity for stresses and pressure scale

So that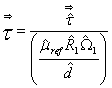; ; dimensionless ; ; ;

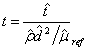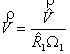The quantities denoted with a hat (ˆ.) are dimensional while quantities without a hat are non-dimensional.

The conservation equations thus become

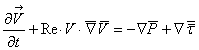(1.3)

The non dimensional corresponding boundary conditions read:

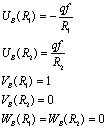
Where the following non-dimensional parameters have appeared

the radius ration; the Reynolds number Re;

;

Rheological behavior

In this work, we consider only the case of shear-thinning fluids, i.e., fluids for which the effective viscosity decreases as the shear rate increases. For the numerical computation, we consider rheological model of Carreau.

The Carreau model is given by :

(1.4)

Where the viscosity at low shear-rat and is the viscosity at high shear rate.

is a time constant of the fluid. The location of the transition from the Newtonian plateau to the shear-thinning regime is determined by 1/. The infinite-shear viscosity is generally associated with a breakdown of the fluid, and is frequently significantly smaller (to times smaller) than . Thus will be neglected in this study.

is the second invariant of the shear rate.

The evolution of as a function is shown in Figures 7 and 8.

It is non dimensional form, the Carreau law leads:

, where

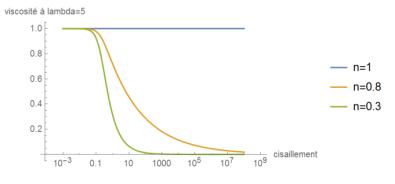
Figure 2. Rheogram for (dimensionless quantities) and varying index n

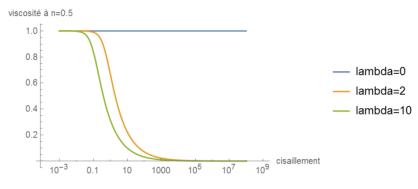
Figure 3. . Rheogram for (dimensionless quantities) and varying lambda

Base flow equations

The flow is considered to be a stationary. Due to the cylindrical symmetry, we have assume that the velocity field is independent of the angle . In order to have a velocity field independent of z , which is requirement to perform a stability analysis hereafter, we ensure a radial flow both at the inner and the outer cylinder. This hypothesis reads:

Where is the radial flow rate per unit height.

We therefore assume the following form of the velocity

.

Mass conservation gives:

;

Which leads to:

considering the boundary conditions

Conservation of momentum leads to:

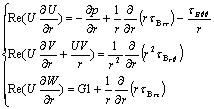(1 .5)

The components of the stress tensor () read :

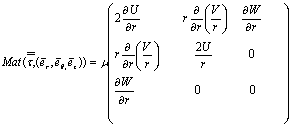
Boundary conditions for the base state:

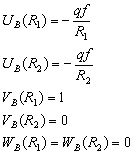
1.2 Numerical resolution

Formulation for collocation points

To solve these equations to non-linear, we turn to a resolution digital. The cylindrical geometry of the problem and the behavior of the fluid to the walls lead us to use a distribution point Gauss-Lobatto.

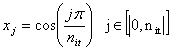
is the number of points selected for the discretization of the space.

Numerical Solution

Since the equation has already been resolved, only two last equations of system are considered and becomes , in matrix form:

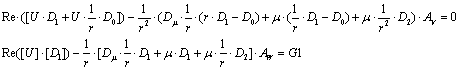
Note that this system is in the form:

At each iteration, the matrices are completely determined. The resolution is therefore up to the inversion of a matrix. These equations are solved in ascending order.

Integration of the boundary conditions

For the resolution of this system , it is necessary to include the boundary conditions.

The translation of matrix is:

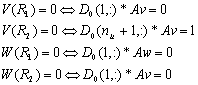
Thus are modified the first and last lines of Kv, Lv, and Lw, Kw of the way in follows:

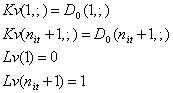
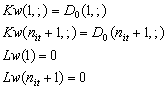
A program implementing this numerical collocation method was thus developed with the software Matlab.

We solve problem for eigenvalues in the particular case of a Newtonian fluid undergoing Taylor-Couette flow. We take the following dimensional parameters:

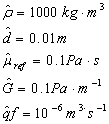
After non dimensionalization, we obtain the following parameters

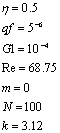
The real part of these values is represented as a function of the imaginary part in figure. On the same figure 17 are plotted the eigenvalues obtained with the program Newtonian taylor Couette of Cherif Nouar and Cecile Lemaitre.

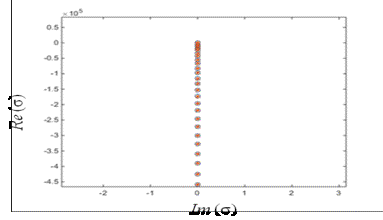
Figure4. -Eigenspectrum of a Newtonian fluid in Taylor-Couette flow.

Real part of eigenvalues vs. imaginary part.

References

1. Steven T. Wereley, Alp Akonur, Richard M. Lueptow, Particle-fluid velocities and fouling in rotating filtration of a suspension, 10 juin 2002

2. D. Martinand, E. Serre. Congrès Français de Mécanique (2013) Bordeaux

3. S. Lee, RM. Lueptow. Journal of Membrane Science (2001) 182:77-90

4. G. I. Taylor. Phil. Trans. Royal Soc (1923) A223, 289–343.

5.Martinand, D., Serre, E., Leuptow, R. Phys. Fluids (2009) 21 104102

6. S. Maretzke, B. Hof, M. Avila. Submitted to Journal of Fluid Mechanics (2014)

7.Young-Ju Kim1, Sang-Mok Han2 and Nam-Sub Woo Korea Institute of Geoscience and Mineral Resources, 30, Gajeong-dong (2013) Flow of Newtonian and non-Newtonian fluids in a concentric annulus with a rotating inner cylinder.

8. L. Guy Raguin, Mark Shannon, John G. Georgiadis, Dispersion radiale et axiale dans les écoulements tourbillonnaires de Taylor-Couette et Poiseuille, 17 juillet 2000.

9. B. Alibeyahia, C. Lemaitre, C. Nouar, and N. Ait-Messaoudene. Revisiting the stability of circular Couette flow of shear-thinning fluids. J. Non-Newtonian Fluid Mechanics, 183-184 :37–51, 2012.