Технические науки/12. Автоматизированные системы управления на производстве.

Соискатель Оганян О.Г.

Национальный политехнический университет Армении, Армения

Корневые годорафы дискретных симметричных систем

автоматического регулирования

На рис. 1 представлена -мерная линейная дискретная многомерная система регулирования, где - дискретная передаточная матрица размера , - период прерывания импульсных элементов, и - -преобразования входных и выходных -мерных векторов, - вещественный скаляр.

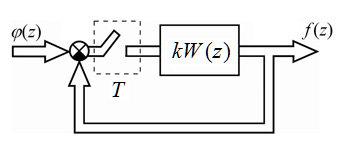
Рис. 1. Матричная структурная схема дискретной многомерной

системы автоматического регулирования

Допустим, дискретная передаточная матрица является простой симметричной, т.е. передаточные функции всех диагональных элементов одинаковы и, кроме того, одинаковы все передаточные функции недиагональных элементов [1-3]. Если обозначить через диагональные, а через все остальные элементы, то простая симметричная матрица может быть записана в виде:

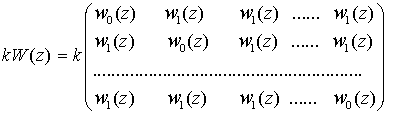. (1)

Рассмотрим, на основе метода характеристических передаточных функций (ХПФ) [1,2], свойства корневых годографов (траекторий корней) дискретной простой симметричной системы с передаточной матрицей (1) при изменении скалярного множителя от нуля до бесконечности.

Устойчивость замкнутой дискретной системы на рис. 1 определяется распределением корней характеристического уравнения

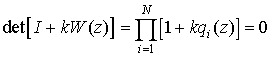, (2)

где называются ХПФ передаточной матрицы (1). Для устойчивости дискретной системы на рис. 1 необходимо и достаточно, чтобы все корни характеристического уравнения (2) находились внутри единичной окружности комплексной плокости [4].

Как известно [1,2], передаточная матрица простой симметричной системы (1) имеет при любом числе каналов только две различные одномерные ХПФ, имеющие вид:

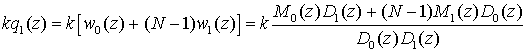(3)

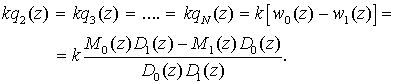(4)

Это значит, что устойчивость дискретной простой симметричной системы определяется только двумя различными характеристическими уравнениями:

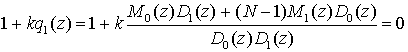(5)

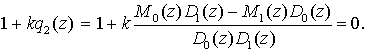(6)

Укажем теперь, что все ХПФ (3) и (4) являются обычными скалярными дискретными передаточными функциями с действительными коэффициентами [3]. Это позволяет сделать важный вывод, что корневые годографы дискретных простых симметричных систем при любом числе каналов можно построить, на основании характеристических уравнений (5) и (6), используя стандартные правила построения корневых годографов обычных дискретных систем регулирования с одним входом и выходом [4].

Отметим, что полюсы всех ХПФ (3) и (4) одинаковы и являются корнями полинома . Кроме того, из (3) и (4) следует, что число нулей всех ХПФ также одинаково, хотя нули ХПФ (3) отличаются от одинаковых нулей всех остальных ХПФ (4). Это означает, что число асимптот траекторий корней для всех одномерных характеристических систем одинаково, однако центры асимптот первой и остальных характеристических систем отличаются. Эти центры определяются по известной формуле [4]:

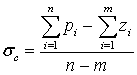, (7)

где и - число полюсов и нулей дискретных ХПФ , а через и обозначены полюсы и нули указанных ХПФ.

Пример. Рассмотрим дискретную простую симметричную систему размера с периодом прерывания и передаточной матрицей

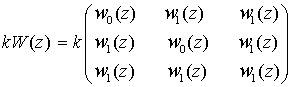, (8)

где

, .

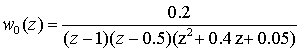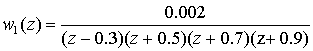Дискретная ХПФ (3) при этом имеет вид

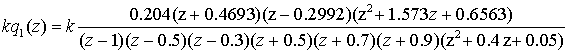, (9)

а одинаковые ХПФ имеют, исходя из уравнений (4), вид

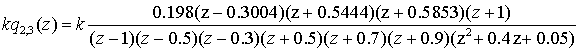. (10)

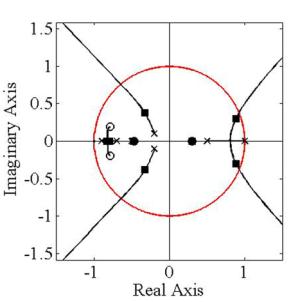
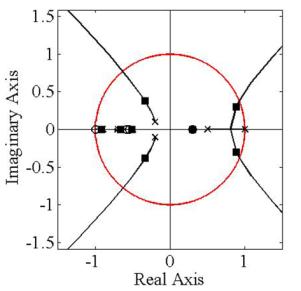
Корневые годографы характеристических систем с дискретными передаточными функциями (9) и (10) показаны на рис. 2, где корни замкнутых характерирстических систем при отмечены черными квадратиками. Как видно из рис. 2, дискретная простая симметричная система с передаточной матрицей (8) устойчива, так как все корни замкнутой системы при находятся внутри единичной окружности. Отметим, что центры асимптот траекторий корней на рис. 2(а) и рис. 2(б) несколько отличаются и равны, соответственно, и .

(а) (б)

Рис. 2. Корневые годографы дискретной системы с передаточной матрицей (8)

СПИСОК ЛИТЕРАТУРЫ

1. Gasparyan O.N. Linear and Nonlinear Multivariable Feedback Control: A Classical Approach, John Wiley & Sons, UK, 2008, 356 P.

2. Гаспарян О.Н. Теория многосвязных систем автоматического регулирования, ГИУА, Ереван, Изд-во «Асогик», 2010, 380 с.

3. Оганян О.Г. Анализ устойчивости дискретных простых симметричных систем (на арм. языке). Вестник, Сборник научных статей, Часть 1, ГИУА, Ереван, 2013, с. 208-213

4. Moudgalya K.M. Digital Control- John Wiley & Sons, UK, 2007.-543с.