д.т.н., доцент Стариченков А.Л.

Федеральное государственное бюджетное учреждение науки Институт проблем транспорта им. Н.С.Соломенко Российской академии наук,

Санкт-Петербург, Россия

Оценка безопасности движения судов с динамическими принципами поддержания на основе анализа их фазовых портретов

Проблема безопасности движения морского подвижного объекта (МПО) непосредственно связана с его устойчивостью. Оценку устойчивости движения судна целесообразно осуществлять на основе анализа его фазового портрета, который позволяет определить области устойчивых и неустойчивых движений рассматриваемого объекта, а, следовательно, прогнозировать возможность попадания судна в аварийные ситуации, связанные с потерей устойчивости. Математически данная задача сводится к предотвращению возможности выхода изображающей точки фазового пространства, характеризующей текущее состояние рассматриваемого объекта, за границу области устойчивости, которая является функцией от коэффициентов математической модели МПО [1]. Проблема прогнозирования устойчивости движения особенно актуальна для судов с динамическими принципами поддержания (СДПП), к которым относятся суда на подводных крыльях (СПК), суда на воздушной подушке (СВП) и экранопланы. Данный класс судов среди других МПО отличают:

1. более высокие динамические характеристики, в том числе и с точки зрения процесса развития аварийных ситуаций;

2. более глубокое и сложное взаимовлияние параметров пространственного положения;

3. большее число разнообразных исполнительных органов (ИО) со сложным характером их взаимодействия;

4. распределенный характер гидродинамических сил и моментов.

В соответствии с рекомендациями работы [2] примем для рассматриваемой схемы СПК концепцию раздельного управления параметрами пространственного положения: параметрами продольного движения – высотой и дифферентом – управляют кормовые внутренние и носовые закрылки, а параметрами бокового движения – рысканьем и креном – управляют руль направления и кормовые наружные закрылки соответственно. Принятая структура дает возможность разделить вектор управления на вектор управления продольным движением

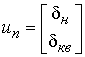
и вектор управления боковым движением

.

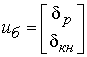В дальнейшем под термином «движение» будем понимать только продольное движение СПК. Любой СПК является многорежимным МПО, т.к. имеет несколько режимов движения. В дальнейшем ограничимся рассмотрением движения СПК только в крыльевом (основном) режиме, учитывая то, что в рассматриваемом режиме можно выделить подрежим маневрирования, заключающийся в целенаправленном изменении курса, высоты движения, крена или дифферента, и подрежим стабилизации параметров положения. Анализ устойчивости движения СПК будем выполнять с помощью линеаризованной модели продольного движения рассматриваемого объекта в виде:

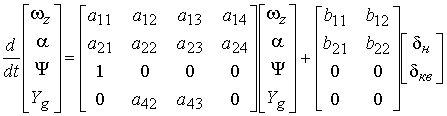, (1)

где - угловая скорость килевой качки, - угол атаки, - угол дифферента, - ордината центра масс СПК, – числовые коэффициенты.

Анализ устойчивости движения СВП в горизонтальной плоскости будем выполнять с помощью взаимосвязанных нелинейных дифференциальных уравнений, описывающих процессы рыскания и бокового сноса для рассматриваемого объекта, которые на основе использования обобщенной математической модели морского подвижного объекта [3] запишем в следующем виде:

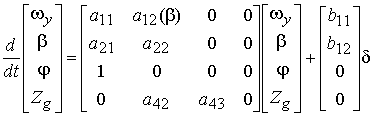, (2)

где – угловая скорость рыскания, – углы дрейфа, курса и перекладки руля соответственно, – боковое отклонение – числовые коэффициенты, причем коэффициент - полином, аппроксимирующий присутствующую в системе нелинейную гидродинамическую зависимость.

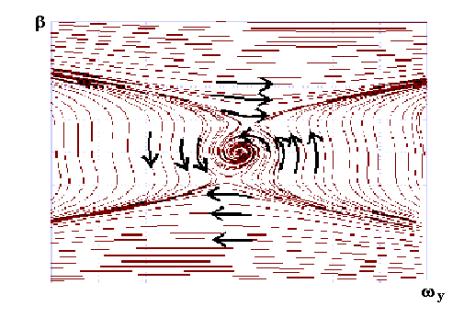
Решив системы дифференциальных уравнений (1) и (2), мы можем построить фазовый портрет горизонтального движения СВП в плоскости параметров состояния (w_y, b) и фазовый портрет продольного движения СПК в плоскости параметров состояния (w_z, a), представленные, соответственно, на рисунках 1 и 2.

Анализируя данные рисунки, можно заметить, что фазовый портрет горизонтального движения СВП содержит три точки равновесия: в начале координат находится «устойчивый фокус», а в I и III квадрантах – неустойчивые точки равновесия типа «седло». Таким образом, для СВП имеет место существование неустойчивого предельного цикла, а область устойчивого движения судна находится в ограниченной области изменения угла дрейфа (b) и скорости рыскания (w_y ).

Рис.1. Фазовый портрет горизонтального движения СВП в плоскости параметров состояния (w_y, b)

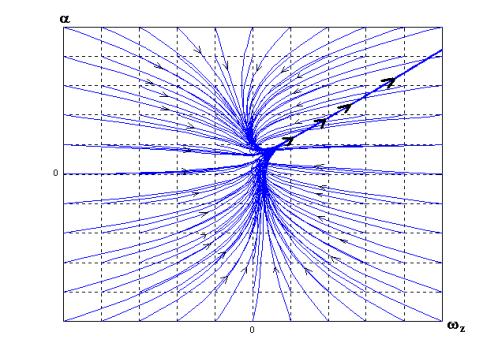
Рис.2. Фазовый портрет продольного движения СПК в плоскости параметров состояния (w_z, a)

Контролируя диапазон изменения значений вышеуказанных кинематических параметров движения СВП, мы можем не допускать возникновения аварийных ситуаций, связанных с потерей устойчивости. Фазовый портрет продольного движения СПК с глубокопогруженными крыльями (ГПК) имеет одну неустойчивую точку равновесия, следовательно, предельные циклы отсутствуют, а неуправляемое движение данного типа МПО является неустойчивым. Фазовые траектории движения СПК, двигаясь по направлению к точке балансировочного режима, достигая ее, как бы, попадают в «воронку», вызывая тем самым неограниченный рост значений кинематических параметров движения. Данный факт свидетельствует о возможности возникновения аварийной ситуации, связанной с собственной неустойчивостью СПК с ГПК по высоте движения и крену, и обусловливает необходимость применения системы управления движением, обеспечивающей автоматическое управление подъемной силой на крыльевом комплексе.

Таким образом, результаты, полученные в ходе анализа фазовых портретов СВП и СПК с ГПК, позволяют сделать вывод о целесообразности прогнозирования устойчивости движения данных МПО на основании анализа их фазовых портретов.

Литература:

1. Стариченков А.Л. Эллиптическая аппроксимация границы области устойчивости бокового движения корабля на воздушной подушке // Навигация и управление движением. Сб. докладов I научно-технической конференции молодых ученых, Санкт-Петербург, ЦНИИ «Электроприбор», 6-7 апреля 1999г. С.161-167.

2. Колызаев Б.А., Косоруков А.И., Литвиненко В.А. Справочник по проектированию судов с ДПП. Л.: Судостроение, 1980, 472 с.

3. Лукомский Ю.А., Стариченков А.Л. Общие закономерности и специфические особенности в математических моделях морских подвижных объектов. // Гироскопия и навигация, №2(17) 1997. – C. 44-52.