Математика/1.Дифференциальные и интегральные уравнения

Abdrakhmanova G.M.

Karaganda economic university of Kazpotrebsouz, Kazakhstan

On Jackson- Nikolskii inequalities in spaces with asymmetric weights Lebesgue

A.A.Markov In 1889, the famous chemist Mendeleev module works at the request of algebraic polynomial algebraic polynomial module assessment proved inequality. In 1951 he inequality for trigonometric polynomial and space (pand q) proved different when S.M. Nikolskii.

Theorema1 (JACKSON- NIKOLSKII INEQUALITIES) Let and is trigonometric polynomials of degree n. Then we have

Definition 1 Let, and for periodically metric function the following integral

,

now it lies on the spaceand is Weights Lebesgue space/

Let () be the space of p power Lebesgueintegrable functions f on equipped with the norm

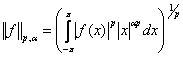
Definition 2 Let and let be arbitrary numbers . The following

(1)

the set of allffunctions is called asymmetric weights Lebesgue space. Denote by . In this paper the following lemms considered.

Lemma 1 Let and let be arbitrary numbers . Theasymmetric weights Lebesgue norm satisfies the conditions:

1. almost everywhere in;

2.

3.

For any positive integer n, let denote the collection of all trigonometric polynomials of degree n, i.e., means that

whereis factor trigonometric polynomial.

Setthe following lemma is valid.

Lemma 4 Letand.The following estimates hold:

a) If, then

(2)

b) If, then

(3)

Proof Let the maximum will be at point . , valid for any

Therefore

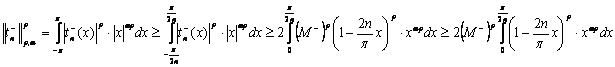
Enough to bring it on inequality.To do this, we use the integral properties

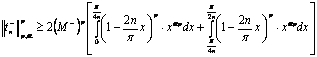
If so, then the perfomed (3) inequality. If , then .

,

Here will the following inequality .

If , then , .

If , then, .

Here will the following inequality

, .

Therefore .

Set . Then has zerosand . Let be the smallest positive zero of the function . We have

Lemma 1 shows that

Therefore

It is enough to convert, to inequality.To do this, we use the properties of the integral.

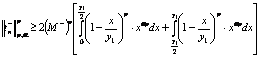
If , then we have inequality (4).If , then.

, .

Consequently .

If , then . Therefore

If , then

Therefore

The proof is complete.

Affirmation 1 Let be arbitrary numbers from . Then we have

(4)

Proof It suffices to prove the following inequality.

(5)

If, then .

If, then

The assertion is proved.

Theorem 2 Let n be a natural number, and let be arbitrary numbers from (1,∞]. Then we have

Here .

Proof We considered separately two cases.

(a) If , then it follows from lemma 2 that

(6)

Under the terms . Therefore

(7)

If , then . Therefore

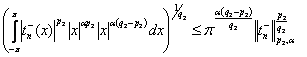(8)

(6)-(8)of inequalities

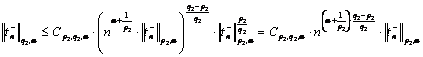(9)

If , , then

(10)

(b) If , then it follows from lemma 4 that

(11)

Under the terms . Therefore .

Of these inequalities .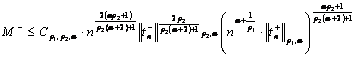

According to the formula

. (12)

Under the terms of the theorem

(13)

If , then . Therefore

(14)

(12)-(13)of inequalities

(15)

(6)-(15)of inequalities, for , we have

.

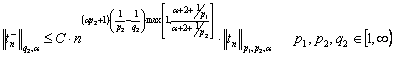References

1. Бари Н.К. «Обобщение неравенств С.Н.Бернштейна и А.А.Маркова»// Изв. АН СССР. Сер. матем., 1954, том 18, выпуск 2, 159–176

2. Никольский С.М. «Приближение функций многих переменнных и теоремы вложения». М., Наука, 1969. с. 133

3. Стечкин С.Б. «Обобщение некоторых неравенств С.Н.Бернштейна» // Докл. АН СССР. 1948. Т.60. №9 с. 1511-1514.

4. Козко А.И. «Аналоги неравенств Джексона-Никольского для тригонометрических полиномов в пространствах с несимметричной нормой» //Матем. заметки, 1997, том 61, №5, С.687 – 689.