MATHEMATICS
/ 3. The probabilities theory and Mathematical Statistics
Iskakova A., Abdenova D.
L.N. Gumilyov Eurasian National University, Astana,
Kazakhstan
Probabilistic
representation of
the generalized exponential distribution of probability
Assume that proper representation
is representable as the value of l0 which distorted by u consisting of their d factors, taking values from the set L1,.., Ld and L1,..,
Ld is independent variables that subordinate the exponential distribution corresponding
parameters λ1, .., λd. Early in works [1] –
[3] one probability model of of generalized of multinomial distribution
of the sum of random values L1, … , Ld, where L1, … , Ld are not observable and observable only their sum.
Assume that Vu represent the number of possible combinations 
that amounting to form u, where 
determine
the possible number of corresponding factors of L1,..,
Ld. In other words Vu is the number of
partitions u, into L1,.., Ld parts.
Theorem 1. The probability of distortion of the value of u determined by the formula
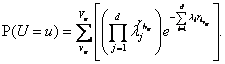(1)
Proof. Let 
is
the space of elementary outcomes of representable model and 
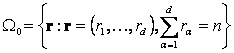is
the space of elementary outcomes of the
generalized exponential distribution, which has appearance
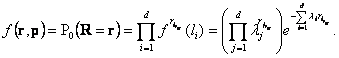
we will consider the following
amount
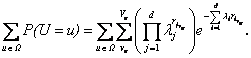
Certainly
if partition u on 
takes place, then partition happens Vu≥1 methods. For each method of partition 
we have a vector 
. It is also obvious that 
is the solution of a system of equations
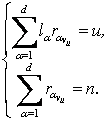(2)
What follows from that the
vector 
corresponds only to one certain 
. Therefore, if 
and 
then 
in case of any
and
. Thus, we have 
Therefore
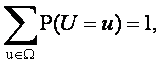
and therefore the considered method of determination of
probabilities on a formula (1) is correct. The theorem is proved.
Exemple.
Let's say that 
where α
accepts any natural numbers on an interval from 1 to d=5. For n=3 we will
define probability P(U=4).
Solving a system of equations
(2) with use of the available data, we receive two partitions of u on l1,…, l5
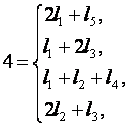
or
Thus,
the probability that the \ variable U will accept value u is
.
REFERENCES
1.
Ayman I. Construction of the most suitable unbiased estimate distortions
of radiation processes from remote sensing data //Journal of Physics:
Conference Series. – IOP Publishing, 2014. – Ò. 490. – ¹. 1. – Ñ. 012113.
2. Ayman I. Statistical Research for Probabilistic Model of
Distortions of Remote Sensing//Journal of Physics: Conference Series. – IOP Publishing, 2016. – Ò. 738.
– ¹. 1. – Ñ. 012004.
3.
Iskakova
A., Ibragimov B. A method for determining an unbiased estimate //
Nauka i Studia. – Przemyśl: Nauka i studia. - NR 7 (52), 2012. –P. 86-91.